Тригонометрические ряды. Ряды Фурье
Тригонометрическим рядом называется ряд вида
(6)
где
- действительные числа.
Рядом Фурье
периодической функции
с периодом
,
определенной на интервале
,
называется ряд (6), коэффициенты которого
определяются по формулам – Фурье:
Если ряд (6) сходится,
то его сумма S(x) есть периодическая
функция с периодом
,
т.е.
.
Теорема Дирихле.
Пусть функция f(x) на интервале
имеет конечное число экстремумов и
является непрерывной за исключением
конечного числа точек разрыва I рода
(т.е. удовлетворяет так называемым
условиям Дирихле). Тогда ряд Фурье этой
функции сходится в каждой точке интервала
и сумма S(x) этого ряда:
1)
во всех точках непрерывности функции
f(x), лежащих внутри интервала
;
2)
на концах интервала, т.е. при
;
3)
,
где
- точка разрыва I рода функции f(x).
Если функция f(x)
задана на интервале
,
где
произвольное число, то при выполнении
на этом сегменте условий Дирихле
указанная функция может быть представлена
в виде суммы ряда Фурье
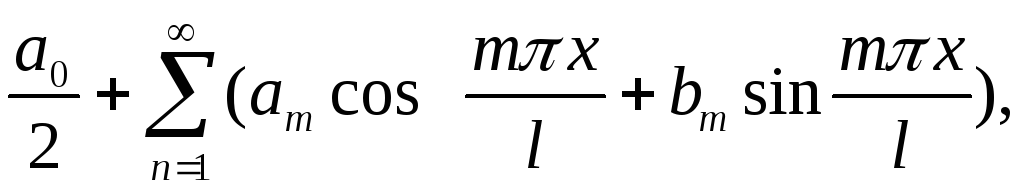
где
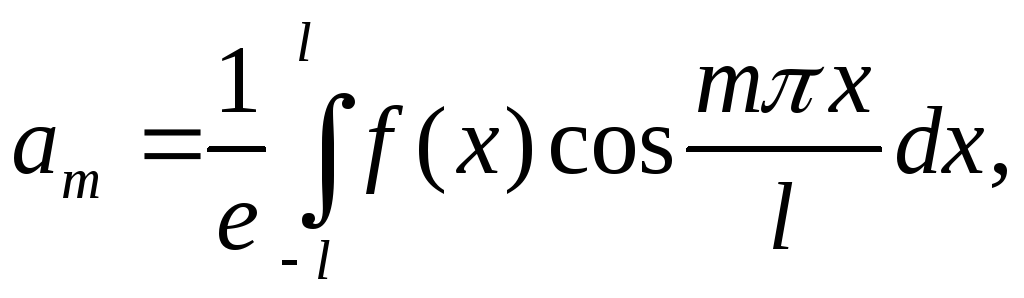
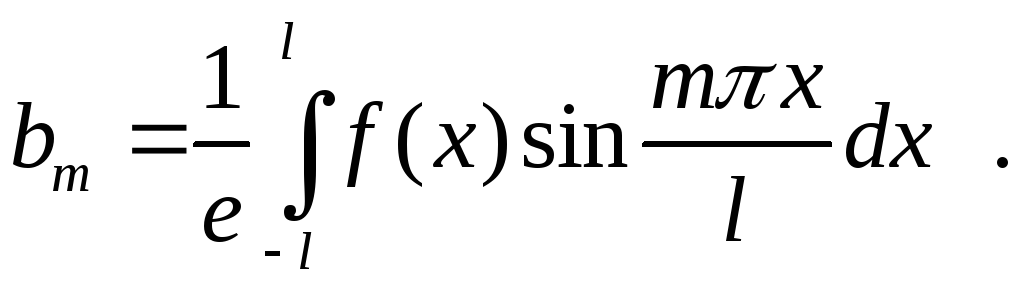
В случае, когда
- четная функция, её ряд Фурье содержит
только свободный член и косинусы, т.е.
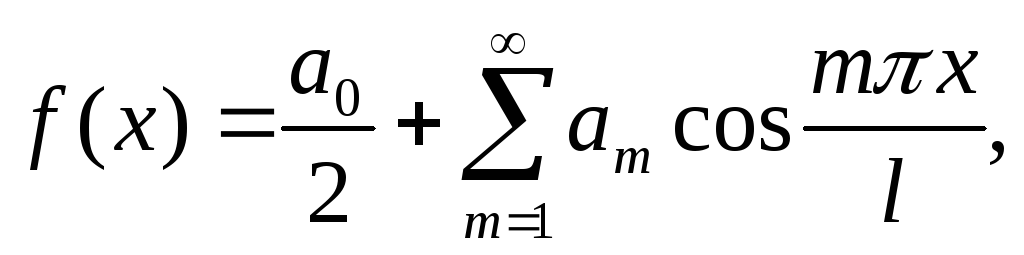
где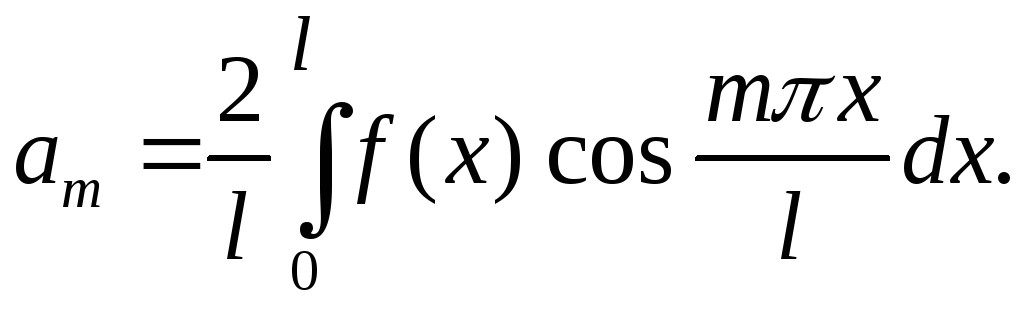 
В случае, когда
- нечетная функция, её ряд Фурье содержит
только синусы, т.е.
где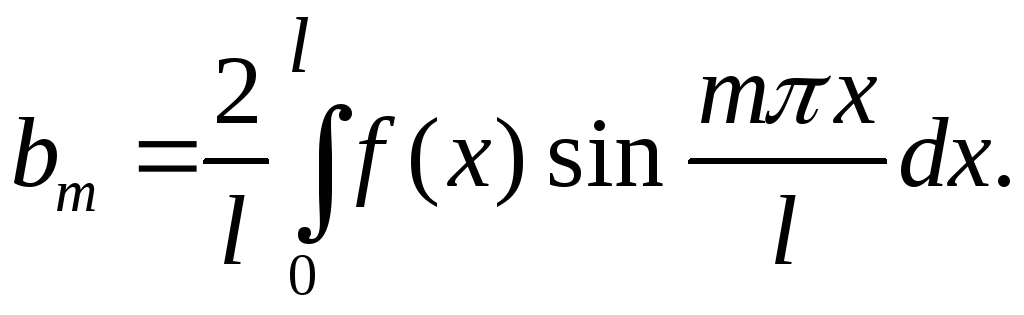 
Если функция
задана на интервале
,
то для разложения в ряд Фурье достаточно
доопределить её на интервале
.
Наиболее целесообразно функцию
доопределить так, чтобы ее значения в
точках интервала
находились из условия
или
.
В первом случае функция
на интервале
будет четной, а во втором – нечетной.
При этом коэффициенте разложения такой
функции (
в первом случае и
-
во втором) можно определить по приведенным
формулам для коэффициентов четных и
нечетных функций.
Пример. Разложить
в ряд Фурье функцию с периодом
,
определенную так
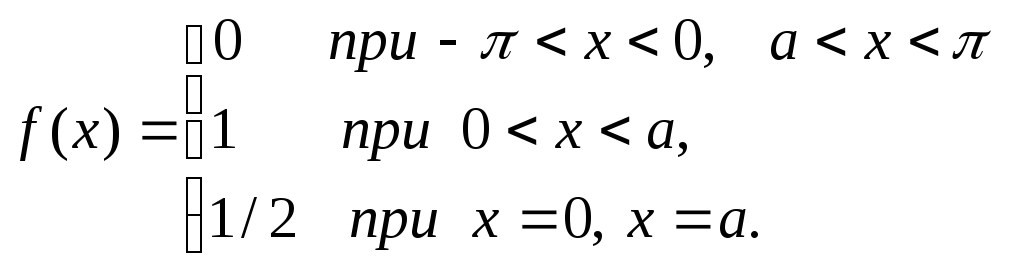
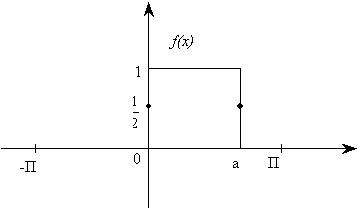
Решение: Из
определения функции
следует, что она удовлетворяет условиям
Дирихле. Поэтому заданная функция
разлагается в свой ряд Фурье.
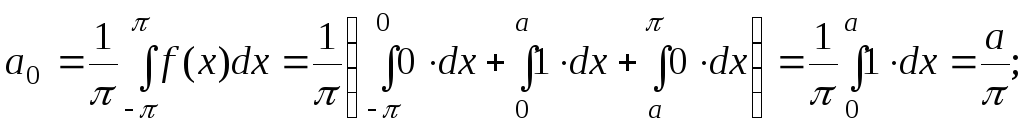
поэтому
Пример. Разложить
в ряд Фурье функцию с периодом
,
определенную равенством.
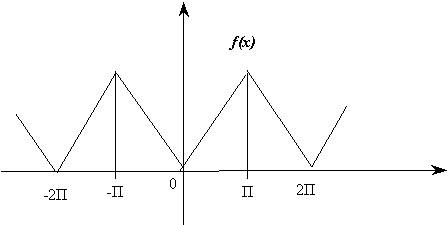
Решение: Эта непрерывная функция, очевидно, удовлетворяет условиям Дирихле и, следовательно, разлагается в свой ряд Фурье, она четная, поэтому
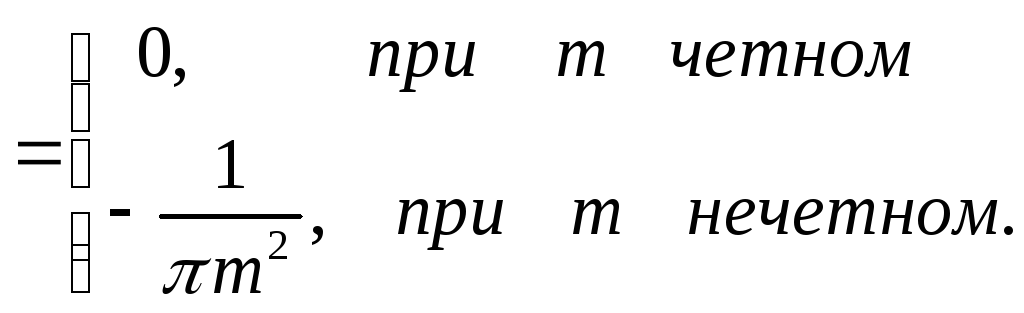
Следовательно,
Пример. Разложить в ряд Фурье функцию определенную равенством
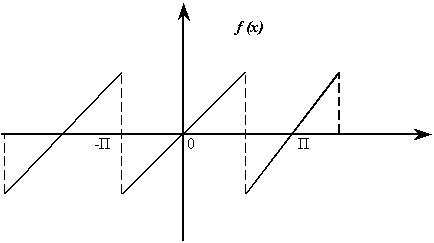
Решение: Эта функция разрывная, удовлетворяет условиям Дирихле, и, следовательно, разлагается в свой ряд Фурье. Функция нечетная, поэтому
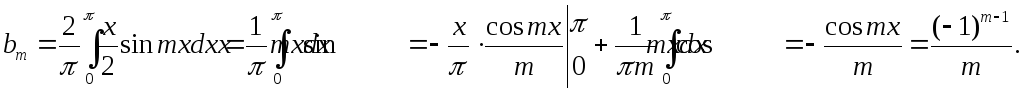
Следовательно
Пример. Функцию
разложить в ряд косинусов на интервале
.
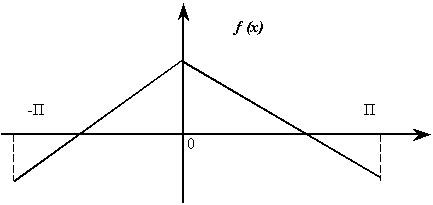
Решение: Продолжая заданную функцию четным образом, как показано на рис. 17 пунктиром, будем иметь
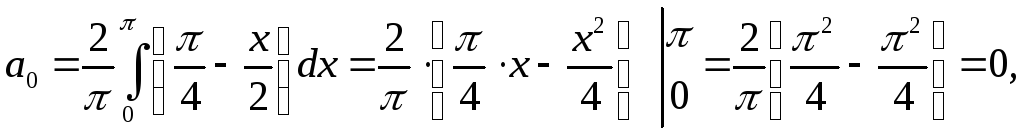
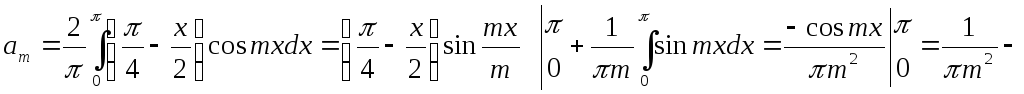
поэтому
Пример. Разложить
в ряд Фурье функцию
с периодом 4, график функции на интервале
– периоде (-2,2) изображен на рис.
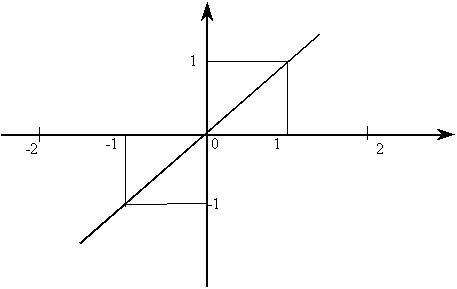
Решение.
Заданная функция нечетная с периодом
2
=4,
поэтому
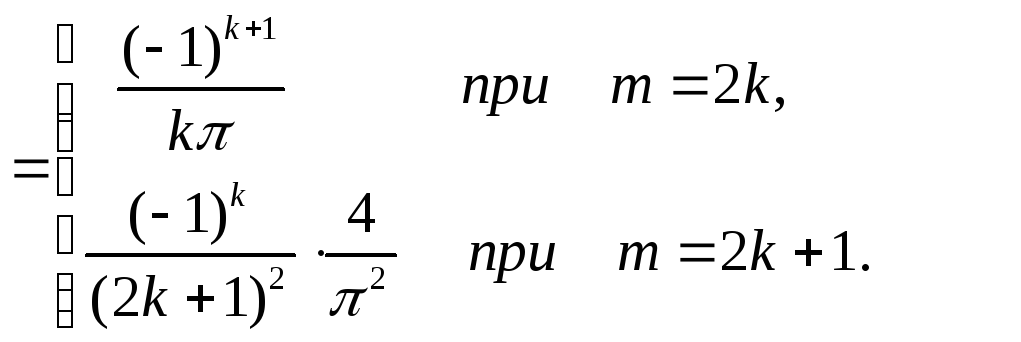
В результате получим
