Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена.

Всякая функция, бесконечно дифференцируемая в интервале т.е. , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора

если в этом интервале выполняется условие

где - остаточный член формулы Тейлора (или остаток ряда),

При получается степенной ряд Маклорена:

Если в некотором интервале, содержащем точку , при любом п выполняется неравенство , где М – положительная постоянная, то и функция f(x) разложима в ряд Тейлора.

Разложение элементарных функций в ряд Маклорена.

;

;

;

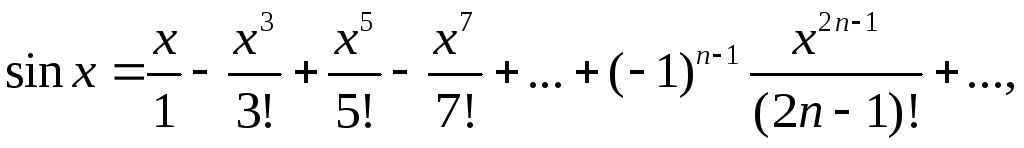
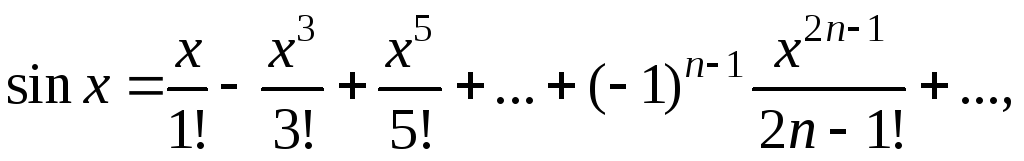
Это последнее разложение имеет место

при

при

при

;

.

Пример. Разложить в ряд по степеням х функцию

Решение: Найдем значения функции и её производных при х =0.

, ,

,

,

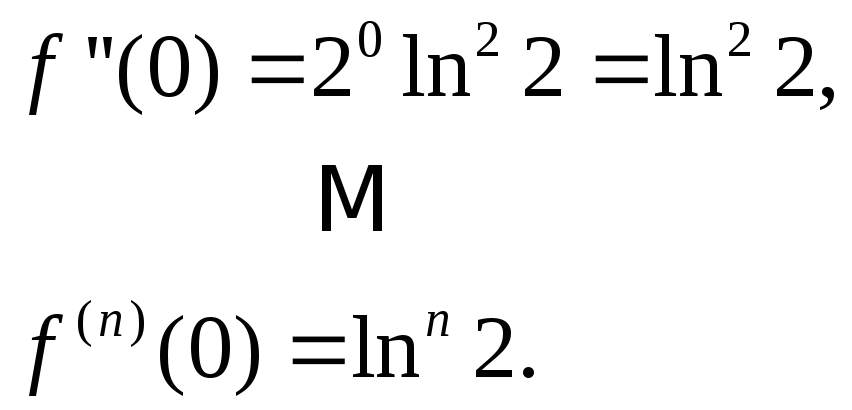
Так как 0 < ln 2<1, то при фиксированном х имеет место неравенство для любого п. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:

,

поэтому

Пример. Разложить в ряд по степеням х функцию

Решение: Продифференцируем функцию п+1 раз:

,

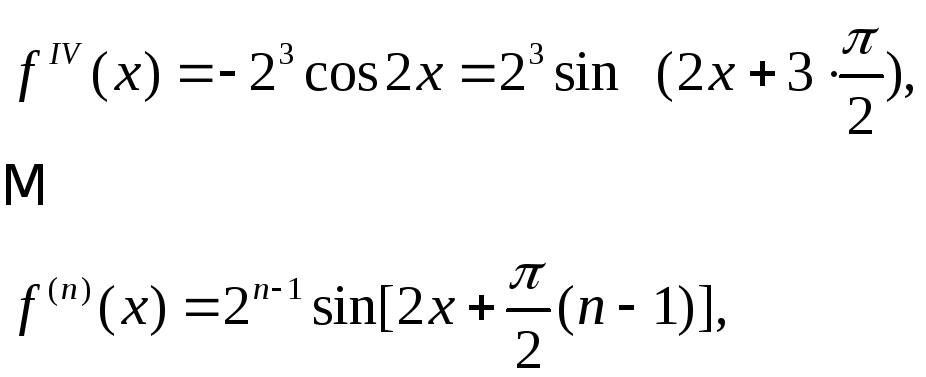
В точке х = 0 находим , а значение f⁽ⁿ⁺¹⁾ (х) определяем в точке х=с. Получаем f(0)=0, ,

Находим остаточный член:

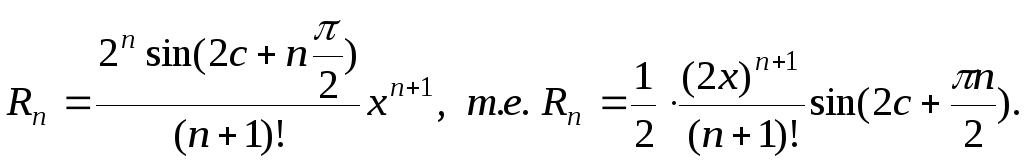
Так как при любом х, а величина ограниченная, то . Следовательно, функцию можно представить в виде суммы ряда Маклорена

.

Пример. Разложить в ряд по степеням х.

Решение: B разложении

_.

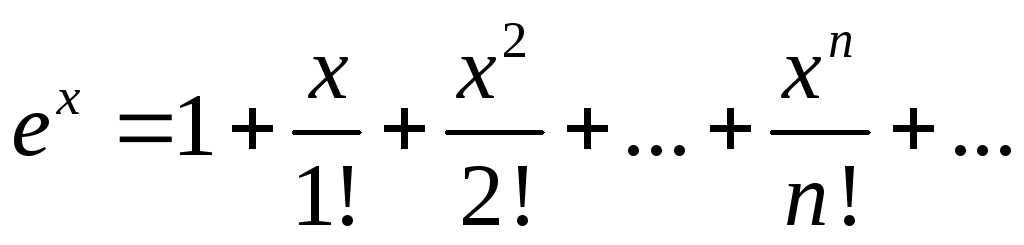
Заменим х на –х²; получим

_.

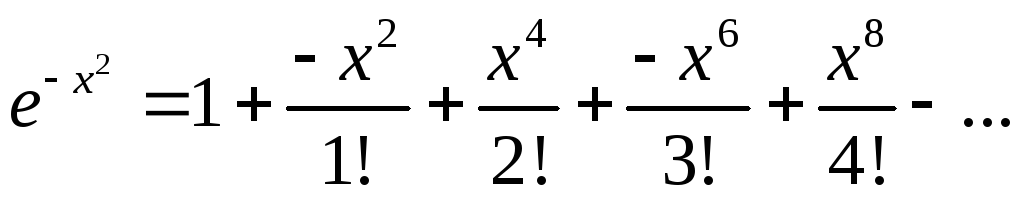
Пример. Разложить lnx в ряд по степеням х -1

Решение: B разложении

.

Заменим х на х - 1; получим

_.

Пример. Разложить в ряд по степеням х -2 функцию 1/х.

Решение: Воспользуемся равенством . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и знаменателем

Отсюда получаем

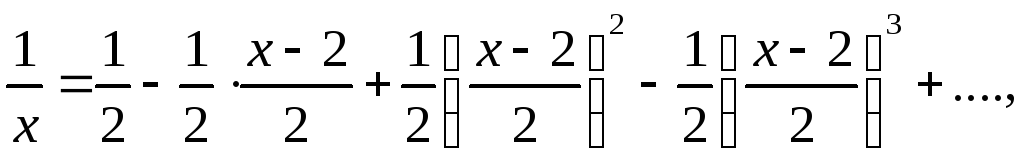
то есть

так как .

Применение степенных рядов.

Разложение в степенной ряд методом интегрирования.

Дифференцируя или интегрируя известные разложения функций в ряд Тейлора, можно получать разложения новых функций в степенные ряды. Так, например, интегрируя

в пределах от 0 до x, |x|<1 (это законно, так как ряд равномерно сходится на отрезке с концами в точках 0 и x при |x|<1), получим формулу ln(1+x)=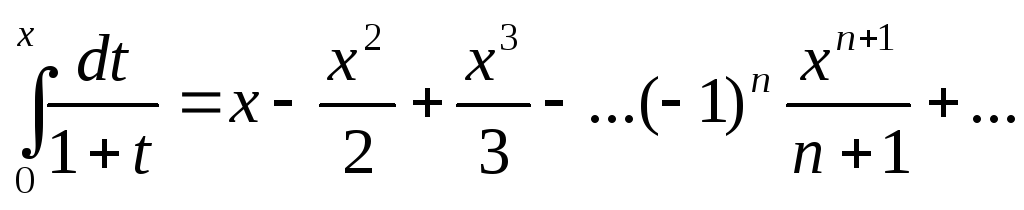

Ряд в правой части сходится при x=1 и, значит, сумма его непрерывна в этой точке.

Пример. Разложить по степеням x функцию arctg x.

Известно, что arctg x=. Разложим подынтегральную функцию в степенной ряд: (из биномиального разложения, полагя t²=x).

Этот ряд сходится для всех значений t, удовлетворяющих неравенствам –1<t<1.

Итак: arctg x =

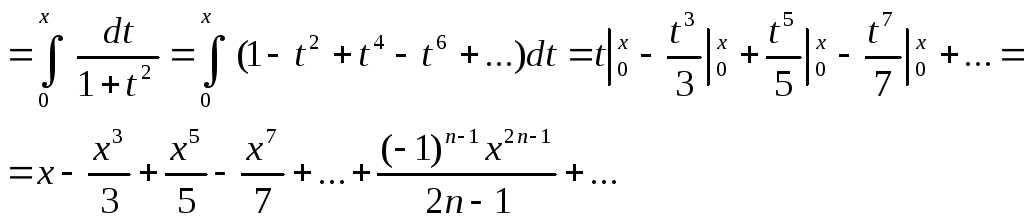
Вычисление значений функций с помощью рядов.

Пусть нужно вычислить значение функции f(x) при x=x₀ с заданной точностью .

Пусть f(x) разлагается в ряд: f(x)=a₀+a₁(x-a)+…+a_n(x-a)ⁿ+… в интервале (a-R, a+R) и точка x₀ принадлежит интервалу.

Тогда, f(x₀)=a₀+a₁(x₀-a)+a₂(x₀-a)²+…

Взяв достаточное число первых членов, получим приближенное равенство, точность которого увеличивается с увеличением n. Абсолютная погрешность |f(x₀)-S_n(x₀)|=|R_n(x₀)|, где R_n(x₀)=a_n+1(x₀-a)ⁿ⁺¹+a_n+2(x₀-a)ⁿ⁺²+…

Необходимо, чтобы |R_n(x₀)|<

Пример 1. Вычислить с точностью до 0,001 число e.

Решение. e^x=

e¹=1+1+

e1+1+

R_n(x)=, где 0<c<x, при x=1

R_n(1)= и так как e^с<e¹<3, получим R_n(1)< и подбором получим, что достаточно n=6 e1+1+.

Приближенное вычисление интегралов.

Пример. 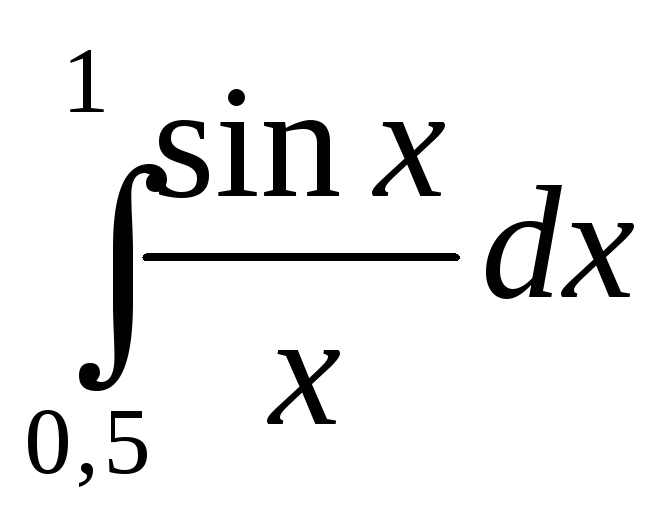с точностью до 0,001.

Так как sinx=x-, то деля почленно на x, получим

Интегрируя

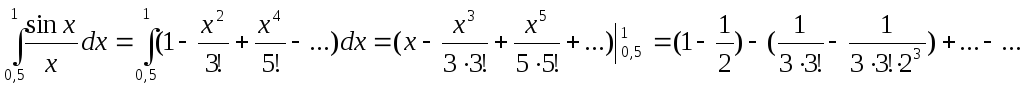
Ряд можно рассматривать как разность сходящихся знакопеременных рядов:

1-

Погрешность не превосходит первого из отброшенных членов, и, подбором, видим, что достаточно трех скобок в разложении

Пример.