§ 3. Неприводимые многочлены.

Многочлен степени с коэффициентами из поля называется неприводимым над полем , если он не может быть разложен в произведение многочленов степеней < с коэффициентами из . В противном случае многочлен называется приводимым над полем .

Неприводимость многочлена зависит от поля, над которым он рассматривается . Так, многочлен приводим над полем и над полем

,

но неприводим над полем рациональных чисел .

Многочлен выше 1-й степени, неприводимый над полем , не может иметь корней в поле . Обратное неверно, т.е., из того, что многочлен не имеет корней в поле , не следует, вообще говоря, что он неприводим над полем . Например, не имеет рациональных корней, но является приводимым над .

Для многочленов степени 2 или 3 обратное верно, а именно, справедливо утверждение: многочлен степени 2 или 3 приводим над полем тогда и только тогда, когда он имеет корень в этом поле.

Всякий многочлен , имеющий степень , разлагается в произведение многочленов, неприводимых над полем , причем, если многочлен двумя способами разложен в произведение неприводимых множителей:

,

то и, при соответствующей нумерации, имеют место равенства , где .

Если в разложении многочлена на неприводимые множители из каждого из этих множителей вынести за скобку старший коэффициент, то получится разложение

, (1)

где все являются неприводимыми многочленами со старшими коэффициентами, равными единице. Для всякого многочлена такое разложение уже однозначно с точностью до нумерации множителей. Если неприводимый многочлен встречается в указанном разложении многочлена раз, то называется -кратным множителем многочлена .

Собирая одинаковые неприводимые множители вместе, можно записать в виде

, (2)

где , если . Таким образом, есть — кратный множитель для . Разложение (2) называется каноническим разложением многочлена над полем .

Более подробно рассмотрим вопрос о неприводимых многочленах над полями и . Необходимые рассуждения основаны на следующей теореме.

Основная теорема алгебры комплексных чисел. Всякий многочлен ненулевой степени над полем имеет хотя бы один корень в поле .

Из этой теоремы следует, что над неприводимыми являются только многочлены первой степени и каноническое разложение многочлена над полем имеет вид:

. (3)

Если многочлен с действительными коэффициентами и — комплексный корень , то сопряженное с число тоже является корнем , причем кратности корней и совпадают. Если в разложении (3) для многочлена перемножить попарно скобки, соответствующие комплексно-сопряженным корням , то получится каноническое разложение над :

. (4)

Квадратные трехчлены, входящие в это разложение, не имеют действительных корней и, следовательно, неприводимы над .

Итак, над полем , кроме многочленов 1-й степени, неприводимыми являются также многочлены 2-й степени, не имеющие действительных корней, а все многочлены выше 2-й степени приводимы.

Пример1. Разложить на неприводимые множители многочлен 1) над полем ; 2) над полем .

Решение. Задача сводится к отысканию корней этого многочлена. Корни этого многочлена найдены в примере 1 (§ 3 пункт 1) и равны . А тогда и есть разложение на неприводимые множители над полем — разложение на неприводимые множители над полем .

Пример2. Разложить на неприводимые множители над полем многочлен .

Решение. Корни найдены в примере 2 (§ 3 пункт 1). Они равны . Поэтому 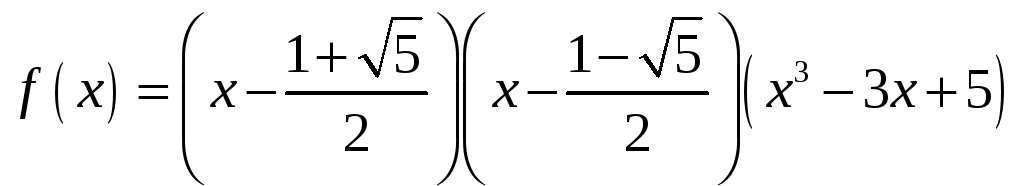является разложением над . Здесь .

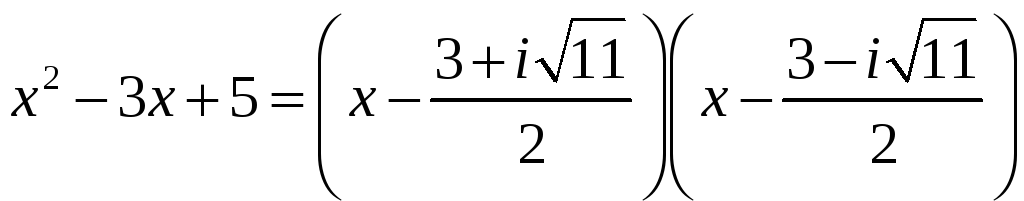Пример 3. Построить многочлен наименьшей степени с комплексными коэффициентами по данным корням: 1 — корень кратности 3; — корни кратности 2; -7 — простой корень.

Решение. .

Пример 4. Построить многочлен наименьшей степени с действительными коэффициентами по данным корням: 2 — корень кратности 2; — простые корни.

Решение. .

В примерах 3 и 4 можно перемножить скобки и получить многочлен в обычной записи.

Остановимся еще на вопросе о неприводимых многочленах над полем рациональных чисел . Пусть — многочлен с целыми коэффициентами.

Критерий Эйзенштейна. Если существует простое число , удовлетворяющее условиям:

1) не делит ;

2) делит ;

3) не делит ,

то многочлен неприводим над .

Если , то неприводим по критерию Эйзенштейна . Неприводимыми над являются также многочлены . Отсюда видно, что для всякого натурального существует многочлен степени неприводимый над , в отличие от полей и .

Литература: — §§ 23, 24, 48, 56;

— § 9.3, 9.4, 11.3;

— № 587, 589, 590, 592, 593, 597, 653.