§ 2. Корни многочленов. Отделение кратных корней.

Если при значении многочлен принимает значение , то число называется корнем этого многочлена.

Число является корнем многочлена тогда и только тогда, когда делится на , т.е. . Если при этом делится на , но уже не делится на , то называется -кратным корнем многочлена . Корни кратности называются простыми корнями многочлена.

Чтобы проверить, будет ли число корнем многочлена и какой кратности, можно воспользоваться схемой Горнера. Сначала делится на , затем, если остаток равен нулю, полученное частное делится снова на и т.д. до получения ненулевого остатка.

Пример 1. Проверить, является ли число корнем многочлена и найти кратность.

Решение. Деление на осуществляем по схеме Горнера

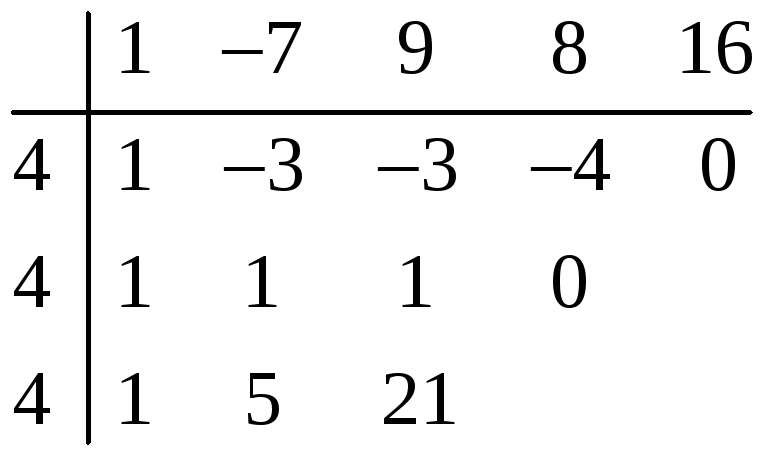
— корень кратности 2.

Пусть — все различные корни многочлена с кратностями, равными соответственно — старший коэффициент . Тогда .Корень многочлена кратности является корнем кратности для его производной. Поэтому , где — многочлен, уже не имеющий своими корнями. Отсюда н.о.д. многочленов и равен .

Следовательно, многочлен имеет числа простыми корнями.

Теперь для отыскания всех корней многочлена достаточно найти все корни многочлена . Это бывает сделать проще, так как степень меньше степени , когда . Построение многочлена называется отделением кратных корней многочлена .

Пример 2. Отделить кратные корни многочлена .

Решение. . Находим . Для этого делим с остатком на :

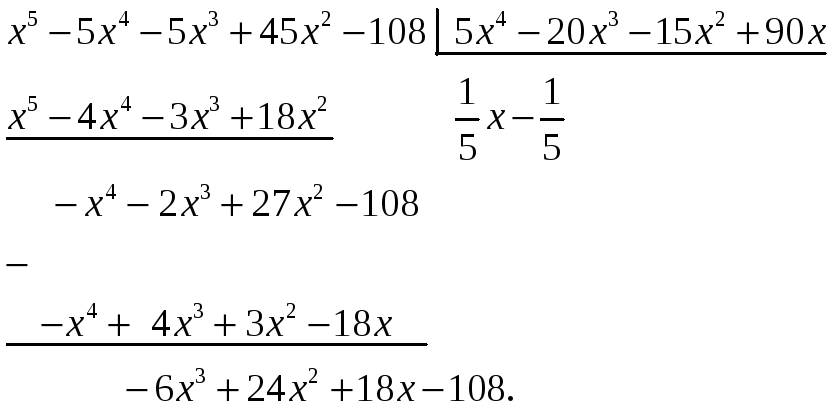
делится на остаток . Поэтому . Искомый многочлен, отделяющий кратные корни , равен .

Заметим, что в примере 2 все корни легко вычислить.

Литература: — § 22, — § 9.4;

— № 555-559, 563-566, 569, 570, 585.

§ 3. Вычисление корней многочлена.

Задача вычисления корней некоторого многочлена часто возникает в практике. Согласно основной теореме алгебры, все корни произвольного многочлена с коэффициентами из числового поля содержатся в поле комплексных чисел . Однако не существует какого-либо универсального метода вычисления этих корней. Метод решения этой задачи зависит от степени многочлена и числового поля . Мы перечислим лишь самые основные методы решения задачи вычисления корней многочлена.

1. Корни многочленов 3-й и 4-й степени.

Если , то для отыскания всех корней многочлена необходимо решить уравнение

(1)

Разделим обе части (1) на . В результате получим уравнение

(2)

имеющее те же корни, что и уравнение (1). Сделаем теперь замену неизвестного . Эту замену проще всего осуществить, представляя многочлен по степеням с помощью схемы Горнера (§ 1) и делая затем замену . В результате замены получим уравнение

(3)

Корни уравнения (3) находятся по формуле Кардано где, 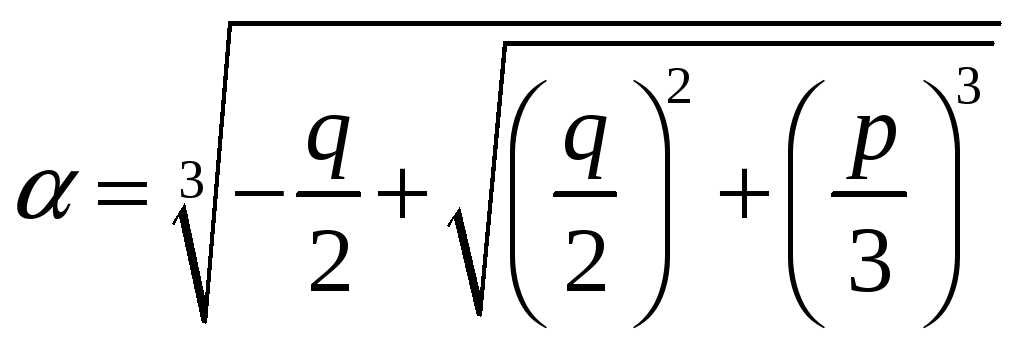, 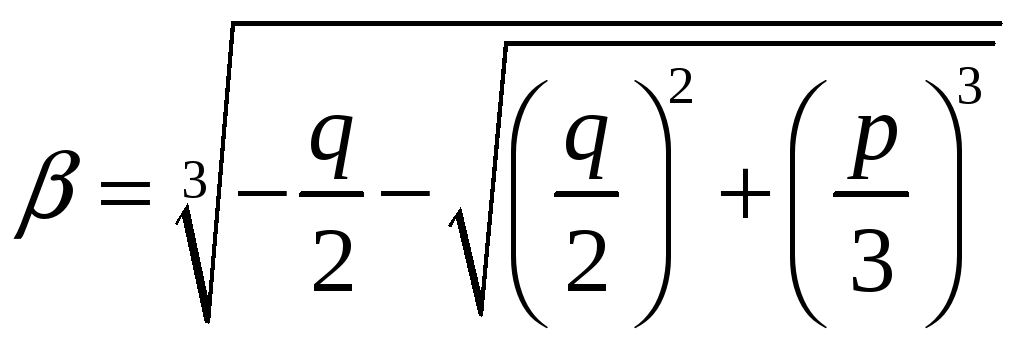(корни извлекаются в поле комплексных чисел ). Применяя эту формулу, нужно для каждого их трех значений брать то значение , для которого выполняется условие (такое значение всегда существует).

Если — все корни уравнения (3), то — все корни уравнения (1) и многочлена .

Пример 1. Найти корни многочлена .

Решение. Разложим многочлен по степеням . Полагая , получим уравнение . Его корни находятся по формуле , где или . Значениями корня являются числа . Соответствующие им значения второго корня Отсюда . Корни многочлена , .

Если — многочлен 4-й степени, то для вычисления его корней достаточно иметь способ вычисления всех корней уравнения вида

(4)

Способ Феррари решения уравнения (4) состоит в следующем.

Левую часть (4) представляют в виде

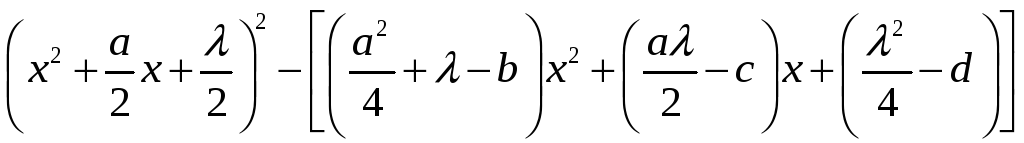, (5)

а затем подбирают так, чтобы выражение в квадратных скобках стало квадратом двучлена первой степени. Для этого необходимо и достаточно выполнение условия

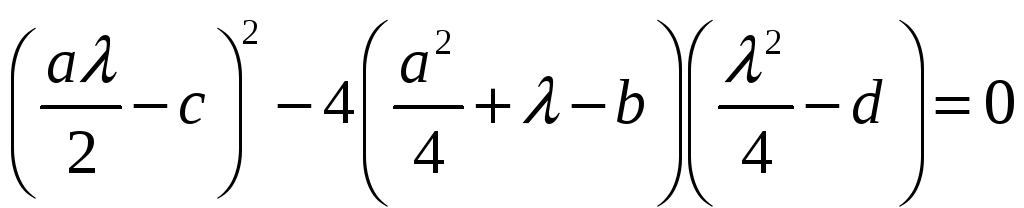, (6)

из которого следует, что является корнем вспомогательного кубического уравнения (6). Теперь находим какой-нибудь один корень и, подставляя его значение в (5), разлагаем левую часть (4) как разность квадратов на множители. Задача вычисления корней сведена теперь к решению двух квадратных уравнений.

Пример 2. Найти корни многочлена .

Решение. Составим уравнение

(7)

Представим левую часть (7) в виде

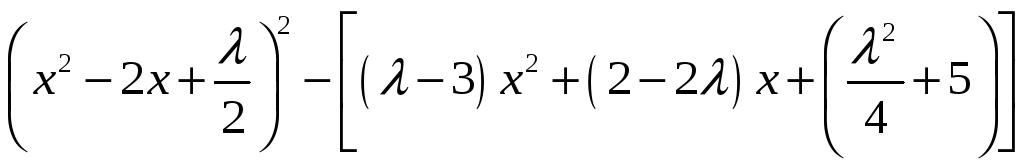(8)

Подберем так, чтобы дискриминант квадратного трехчлена в квадратных скобках был равен нулю:

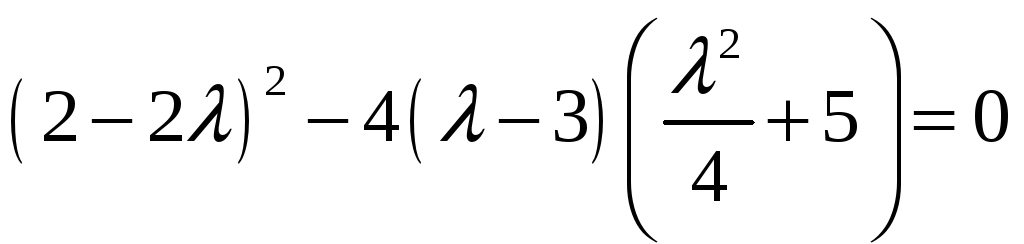
или

.

Можно заметить, что 4 — один из корней этого уравнения. Тогда подставим в (8) и уравнение (7) примет вид:

или

.

Отсюда, решая уравнения и , получим корни нашего многочлена

Литература: — § 38, — № 167, 173, 174.

2. Рациональные корни многочленов с рациональными коэффициентами.

Многочлен имеет те же корни, что и многочлен с целыми коэффициентами, полученный из умножением на общее кратное знаменателей всех коэффициентов .

Если несократимая дробь является корнем многочлена с целыми коэффициентами, то выполняются следующие условия:

1) — делитель числа ;

2) — делитель числа ;

3) для любого целого числа число является делителем числа .

Поэтому все рациональные корни многочлена (если они существуют) нужно искать среди несократимых дробей, удовлетворяющих условиям 1, 2, 3.

Если , то все рациональные корни являются целыми числами.

Пример. Найти рациональные корни многочлена и определить их кратность.

Решение. Если — несократимая дробь, является корнем , то делит 12, а делит 2. Все делители 12: , а делители 2: 1,2.

Зафиксируем . Тогда по (3) условию . В качестве возьмем и . Тогда и . . . Числа 1 и -1 не являются корнями. Если число — корень, то и . Такому условию удовлетворяют -2, 4. С помощью схемы Горнера выясняем, что число -2 является корнем кратности 2.

Далее, зафиксируем . Тогда и (). Проверять надо лишь взаимно простые с , т.е., . Среди этих чисел условию () удовлетворяют -1, 3. Проверяя по схеме Горнера дроби и выясняем, что корнем является . Итак, — простой корень, — корень кратности 2.

Литература: — § 57, — § 11, 3, — № 649-651.