Семинар №13

Задачи и упражнения

1. Исследуйте поведение системы, описываемой следующим нелинейным разностным уравнением: 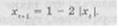 В качестве начального значения X1 возьмите все более точные значения л/4. При X1 - 0,7 у системы появится предельный цикл с периодом 2, при Jr1 = 0,78 - цикл с периодом 10 и т.д. Задав X1 = л/4, получим хаотический режим [3]. Учтите, что в Excel число п задается функцией = ПИ ( ), а модуль числа х записывается как ABS(X).

2. Попробуйте варьировать значения параметров модели из задачи 1.

3. Проведите вычислительные эксперименты с разностными аналогами системы Лотки-Вольтерра, варьируя типы взаимодействий.

4. Исследуйте разностное уравнение X1^1 = 3,6 xt - *(2при О < X1 < 3,6. Имеет ли система хаотический режим?

5. Исследуйте разностное уравнение с запаздыванием: о появлении новых универсальных моделей реальности [1], созданы даже машины клеточных автоматов - приставки к ЭВМ, существенно ускоряющие процесс моделирования [5].

Темы рефератов:НЕТ

Глава 13. Модели хаоса и катастроф

13.1. Математическая модель катастрофы "сборка"

Рассмотрим основные положения теории катастроф на примере катастрофы "сборка", которой соответствует дифференциальное уравнение

dx/dt = -х3 +Ьх+а.        (13.1)

При варьировании значений параметров а и & поведение системы (число стационарных точек, их расположение) будет также меняться. Для изучения качественного характера этих изменений рассмотрим потенциальную функцию

F(x,a,b) = х4 /4 - bx2 /2 - ах.

Заметим, что -dF/дх = -х* +bx+a. Ha рис. 13.1 приведены двухмерные графики, характеризующие поведение функции F.

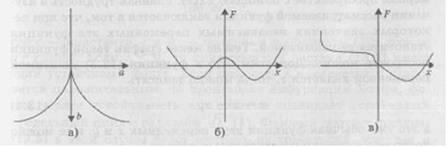
На рис 13.1,а изображена так называемая бифуркационная кривая (4Ь3 - 27а2). Эта кривая разделяет плоскость (а, Ь) на две части. Внутри кривой функция F имеет два минимума (рис. 13.1,6). За пределами этой кривой функция F имеет только один минимум (рис. 13.1,в). Как известно, экстремальные значения функции F можно определить, приравняв нулю первую производную:

х3-Ьх-а = 0.        (13.2)

Целесообразно также провести исследование функции г, построив серию графиков при фиксированных значениях у из интервала (-5;5).

Как указывалось в § 12.3, основными характеристиками фазового портрета на плоскости являются положения равновесия и предельные циклы. Сепаратрисы связывают седловые положения равновесия с особыми точками и предельными циклами. Если менять параметры структурно-устойчивой системы, то ее фазовый портрет будет также меняться, но его топологическая структура в определенном диапазоне значений параметра будет оставаться постоянной. При достижении критических значений параметров происходит бифуркация - меняется топологическая структура фазового портрета. Качественное исследование динамической системы, зависящей от параметров, предполагает описание всех возможных в ней бифуркаций и определение множества бифуркационных значений параметров.

Рассмотрим системы, зависящие от одного параметра. Вернемся к рис. 12.5, на котором изображены типичные фазовые портреты в окрестности точки равновесия. В двух случаях положение равновесия является устойчивым: устойчивые фокус и седло, и в трех - неустойчивым: седло и неустойчивые узел и фокус.

Если в процессе изменения системы параметр подходит к бифуркационному значению, то либо два положения равновесия сливаются и "умирают" (система совершает скачок, перескочив на другой режим), либо "рождается" пара положений равновесия. Причем из двух положений равновесия одно устойчиво, а другое неустойчиво.

Ситуация возникновения предельного цикла может быть проиллюстрирована следующей системой уравнений:

\dr/dt = Kr-r3;        (135)  [dy/dt = с ,

где с - константа, гиф - полярные координаты (х = rcos ср; j/ = rsintp). Если А, < О, то динамическая система (13.5) имеет один устойчивый фокус. Если параметр А. изменяется и становится положительным, то происходит бифуркация Хопфа, фокус теряет устойчивость и в системе возникает устойчивый предельный цикл с радиусом >/Х [1]. Фазовый портрет системы (13.5) в этом случае будет состоять из траекторий, изнутри и снаружи "наматывающихся" на предельный цикл. Это означает, что независимо от начального состояния система достаточно быстро перейдет в режим периодических колебаний (автоколебательный режим).

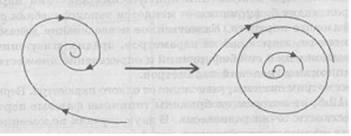
Рис. 13.3. Рождение цикла

Рассмотрим бифуркации, связанные с предельными циклами. В этом случае возможны два варианта. При первом варианте из устойчивого фокуса при изменении параметра рождается устойчивый предельный цикл (рис. 13.3). В случае второго варианта при изменении параметра неустойчивый предельный цикл исчезает, и его неустойчивость передается положению равновесия - фокусу (рис. 13.4).

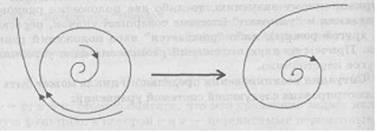
Рис. 13.4. Гибель цикла

В первом варианте после потери устойчивости положения равновесия устанавливается колебательный периодический режим (мягкая потеря устойчивости). Во втором варианте система уходит со стационарного режима скачком (жесткая потеря устойчивости) и переходит на другой режим движения [1].

Множество точек, к которым притягиваются траектории автономных систем, называется аттрактором. Для систем с двумя переменными существует только два типа аттракторов - особая точка и предельный цикл. В первом случае все изучаемые величины с течением времени выходят на постоянные значения, во втором - на периодический режим.

При количестве переменных в системе N > 3 и наличии в правой части только линейных и квадратичных членов возможно возникновение странных аттракторов.