§ 13. Корреляция. Корреляционный момент и коэффициент корреляции. Уравнение регрессии

В § 12 мы познакомились с понятием вероятностной зависимости и определили ее как такую зависимость, когда с изменением случай­ной величины X изменяется закон распределения случайной величины Y. Как мы уже знаем, закон распределения, например, для непрерыв­ной случайной величины задается кривой распределения у(х). В за­висимости от того, что изменяем в выражении у(х) - ее вид или только некоторые числовые характеристики, - различают несколько типов вероятностной зависимости. Одним из наиболее распространен­ных типов такой зависимости является так называемая корреляцион­ная зависимость, при которой с изменением х изменяется математиче­ское ожидание у (рис. 23, а и б). Оба рисунка иллюстрируют эту за­висимость, причем в первом случае изменение My происходит непрямо­линейно (криволинейная корреляция), а во втором - по закону пря­мой линии (прямолинейная корреляция). Эту последнюю зависимость часто называют для краткости корреляцией. Если зависимость между X и Y будет установлена и выражена формулой, то ее можно исполь­зовать для надлежащей организации и обработки результатов экспе­римента, например, измерений.

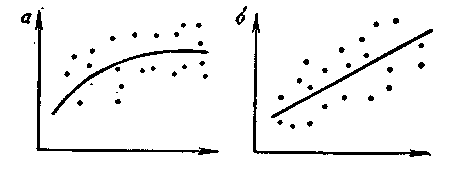
Рисунок 23.

Систему двух случайных величин, как и одну случайную величи­ну, кроме задания закона совместного распределения, определяют еще числовыми характеристиками, так называемыми специальными начальными и центральными моментами порядка s, q.

. (1.87)

В частном случае, очевидно, имеем

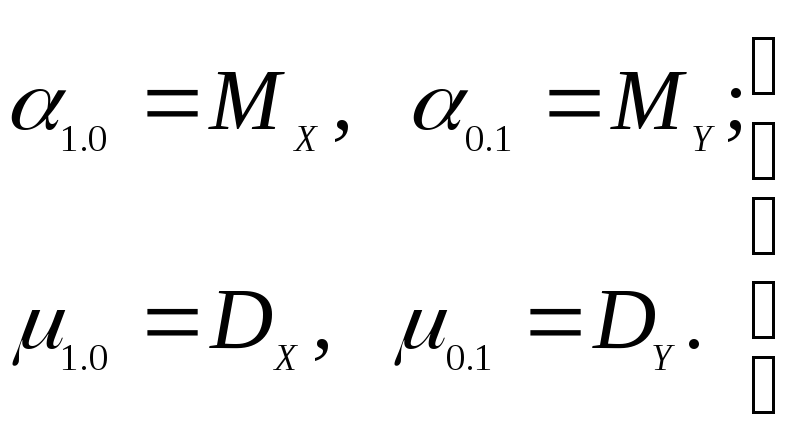(1.88)

В теории корреляции важнейшее значение имеет центральный смешанный момент второго порядка

(1.89)

который называют корреляционным моментом и обозначают K_xy .

Его вычисляют по формулам

(1.90)

(1.91)

соответственно для прерывных и непрерывных случайных величин.

Момент K_xy как раз и характеризует силу, тесноту корреляции. Однако его значение зависит еще и от размерности случайных вели­чин. Для того чтобы освободиться от последней, вычисляют так на­зываемый коэффициент корреляции

(1.92)

который численно характеризует силу корреляции в чистом виде.

Коэффициент корреляции изменяется в пределах -1 ≤ r ≤ 1. Когда он равен +1 или -1, между х и у существует прямолинейная зависимость (рис. 24. а и б) у = ах + b.

Рисунок 24.

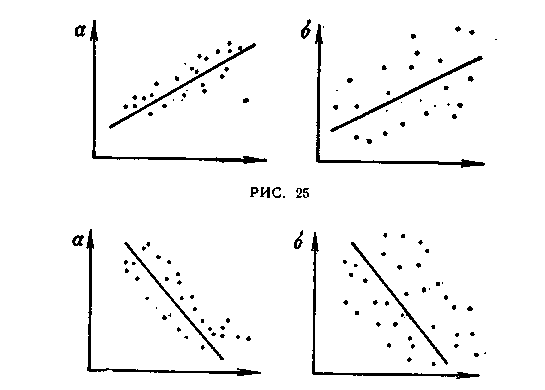
Рисунок 25.

Рисунок 26.

В случае r < 0 имеет место отрицательная корреляция с умень­шением (увеличением) X величина Y имеет тенденцию увеличивать­ся (уменьшаться); при r > 0 говорят о положительной корреляции- с уменьшением (увеличением) X величина Y имеет тенденцию умень­шаться (увеличиваться).

На рис. 25 показана положительная корреляция, причем в первом случае она более тесная, чем во втором (r₁ > r₂), а на рис. 26 — от­рицательная корреляция, более тесная также в первом случае.

Если случайные величины X и Y независимы, то корреляционный момент K_xy = 0 (также с r_XY = 0).

Две корреляционные случайные величины также и зависимы. Об­ратное утверждение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некорре­лированными.

В том, что две зависимые величины могут быть некоррелированны­ми, легко убедиться на следующем примере.

Пусть поверхность распределения задана в виде внут­ри эллипса и вне его. Найдем корреляцион­ный момент по формуле

.

Так как плотность распределения

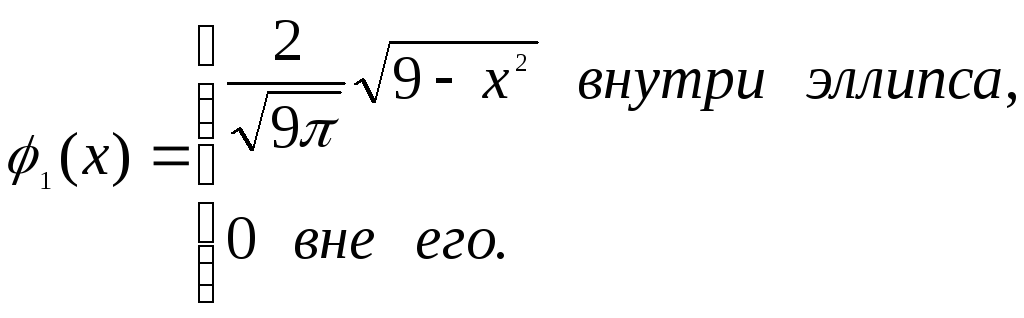
симметрична относительно оси Oу, то М_х = 0, аналогично M_Y = 0, так как плотность

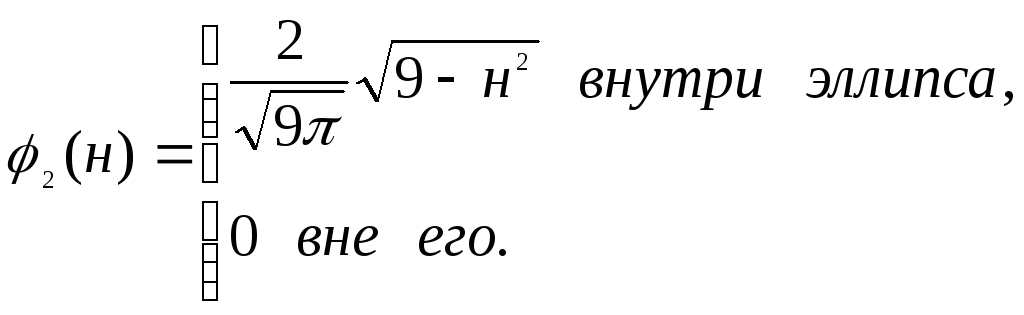
симметрична относительно оси х. Поэтому

Учитывая, что f (xy) не содержит переменных, получим

Внутренний интеграл равен 0 (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала коорди­нат). Следовательно, K_xy = 0, т. е. x и у некоррелированы, однако зависимы, так как φ(xy) ≠ φ₁(x) φ₂(y).

На практике часто встречаются двухмерные случайные величины, распределение которых нормально. В этом случае

,

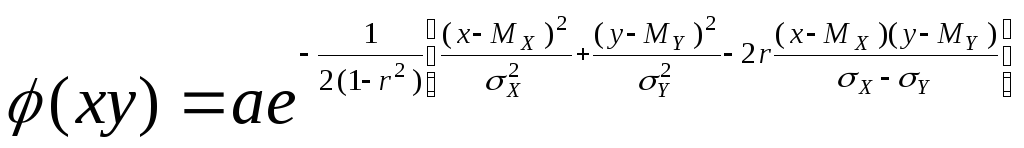где , а так называемая экспонента ехр с = е^c.

При нормальном законе распределения из некоррелированности следует и независимость х и у. В самом деле, пусть r_XY = 0. Тогда

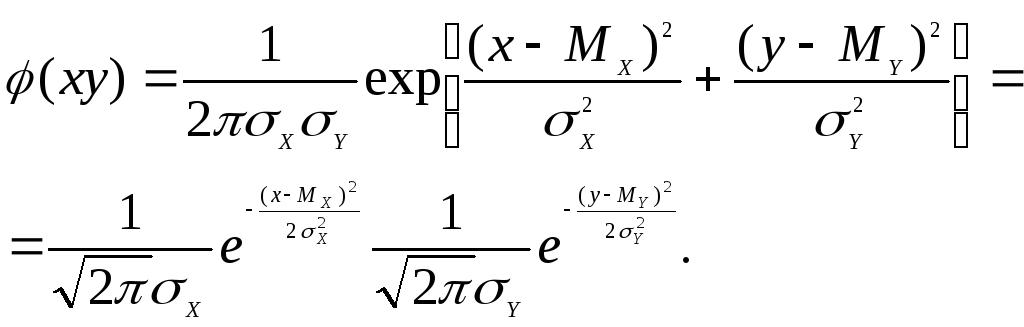
что и означает независимость случайных величин х и у.

Таким образом, если две случайные величины подчинены нормаль­ному закону распределения, то некоррелированность и независимость понятия тождественны.

Корреляционную зависимость, кроме задания ее тесноты, необхо­димо характеризовать формой.

Форма прямолинейной связи между X и Y выражается в виде так называемого уравнения регрессии Y на X

(1.93)

или

(1.94)

где коэффициент

(1.95)

- коэффициент регрессии у на х. На рис. 25, 26 сплошные линии являются уравнениями регрессии.

Существует уравнение регрессии х на у, имеющее вид

где

1.222. Доказать, что если случайные величины х и у независимы, то корреляционный момент К_хy = 0.

Р е ш е н и е. Воспользуемся формулой (1.91). Имеем для независимых величин

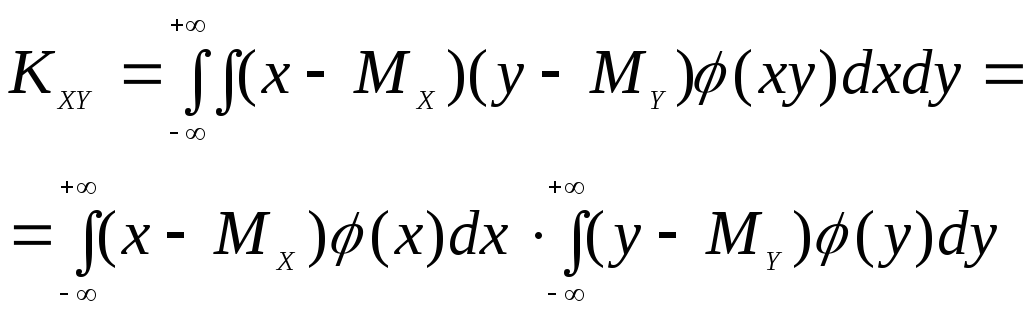(1.96)

Но интегралы - сомножители в формуле (1.96) представляют собой центральные моменты первого порядка, равные нулю. Поэтому K_XY = 0.

1.223. Доказать, что корреляционный момент

К_XY = М [(х – М_X)(у – М_Y)] (1.97)

можно представить в виде

К_XY = М_XY – М_X М_Y (1.93)

У к а з а н и е. Раскрыть скобки в выражении (1.97) и воспользоваться свойствами математического ожидания.

1.224. Доказать, что если между величинами X и Y имеет место функцио­нальная зависимость вида у = ах + b, то коэффициент корреляции | r | = 1.

Доказательство. Имеем М_Y = а М_X + b.

Поэтому для корреляционного момента получим

Дисперсия D_Y = а²σ² (по свойствам дисперсии (1.39 - 1.40), откуда σ_Y = σ_Y | a | σ_X. (величина а взята по модулю, так как по определению стандарт - вели­чина всегда положительная). Поэтому

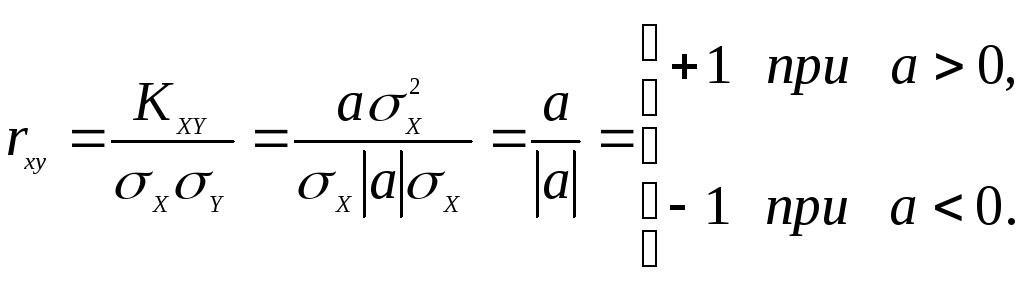
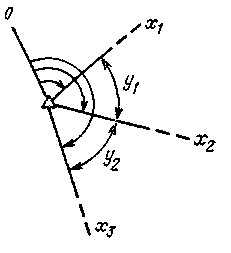
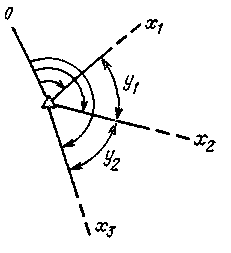
Рисунок 27.

1.225. Имеются три независимые случайные величины Z₁,Z₂ и Z₃ с известными математическими ожиданиями и с. к. о. . Найти коэффи­циент корреляции между функциями

X = Z₁ + Z₂ , Y = Z₁ + Z₃;

и написать уравнение регрессии y на x.

Решение. Имея в виду формулы (1.92) и (1.98), находим, пользуясь свойствами матема­тического ожидания (1.35).

.

Поэтому на основании (1.45). Следовательно,

На основании свойства дисперсии для независимых величин имеем и Поэтому

.

Если _, то

В этом случае уравнение регрессии будет у = M_Y + 0,5(x - М_х) .

226. Доказать, что коэффициент корреляции между двумя углами у₁ и у₂, измеренными способом круговых приемов (рис. 27), равен r = - 0,5. Объяс­нить, что вызывает корреляцию этих углов. Построить уравнение регрессии у₂ на у₁ и у₁ на у₂.

227. Плотность распределения двухмерной случайной величины задана формулой

Найти с. к. о. σ_X, σ_Y и коэффициент корреляции r_xy.

Ответ: σ_X = √2.

1.228. Найти коэффициент корреляции и написать уравнение регрессии у₂ на у₁, если y₁ = x₁ , у = х₁ - х₂, а .