Аргумент комплексного числа визначається виразом . ( 2 )

Для того , щоб перевести комплексне число з алгебраїчної форми в тригонометричну , потрібно визначити косинус та синус аргументу φ :

( 3 ) ( 4 )

З тригонометричної форми комплексного числа легко перейти до показникової .Для цього визначають модуль та аргумент комплексного числа за формулами ( 1 ) , ( 3 ) та ( 4 ) .

Приклад 9.1 .

Дано : а = 3 ; в = 4 .

Комплексне число в алгебраїчній формі має вигляд : А = 3 + j4

Знаходимо модуль числа :

Аргумент числа :

Комплексне число в тригонометричній формі : А = 5 ( Соs 53^o10 + j Sin 53^o10)

Побудуєм вектор комплексного числа :

j

4 А = 5

53^о10 + 1

3

Рис. 9.5.

Комплексні числа можна додавати , віднімати , множити та ділити. Додавати та віднімати простіше у алгебраїчній формі , а множити та ділити - у показниковій .

Приклад 9.2.

Знайти суму та різницю двох комплексних чисел А = 2 + j 3 ; B = 6 – j 9 .

Сума чисел : А + В = 2 + j 3 + 6 – j 9 = 8 – j 6 ;

Різниця чисел : А – В = 2 + j 3 – 6 – ( - j 9 ) = - 4 + j 12 ;

Приклад 9.3.

Знайти добуток та частку чисел А = 4 + j 3 , B = 6 – j 8 .

Переведемо комплексні числа А і В із алгебраїчної форми в показникові:

Приклад 9.4.

Перевести комплексне число А з показникової форми в алгебраїчну.

Спочатку переведемо показникову форму числа в тригонометричну, а потім в алгебраїчну:

Методику та послідовність розв’язання розрахункового завдання № 9 розглянемо на прикладі 9.5. Приклад 9.5.

До затискачів кола змінного струму приведеного на малюнку 9.1. прикладена напруга . Повні опори ділянок кола дорівнюють: Z₁=5+j5Ом; Z₂=5Ом; Z₃= – j6Ом; Z₄=3+j6Ом;

Визначити струми у вітках та струм у нерозгалуженій частині кола, повну, активну та реактивну потужності кола. Побудувати векторну діаграму в осях комплексних чисел.

Рис. 9.5.

Розв'язок

Задачу розв'язуємо у символічній формі методом згортання кола.

1. Визначаємо опір послідовного з'єднання опорів Z₂ та Z₄

Z₂₄= Z₂+ Z₄=5+3+ j6=8+ j6=10е ^j36,87º Ом

2. Визначаємо опір паралельного з’єднання Z₂₄ та Z₃

3. Еквівалентний опір кола дорівнює:

Z_екв= Z₁+ Z₃₂₄=5+j5+7,5е^–j53,13º=5+j5+4,5–j6=9,5–j1=9,55е ^-j6º Ом

4. Визначаємо струми у вітках та нерозгалуженій частині кола.

А

В

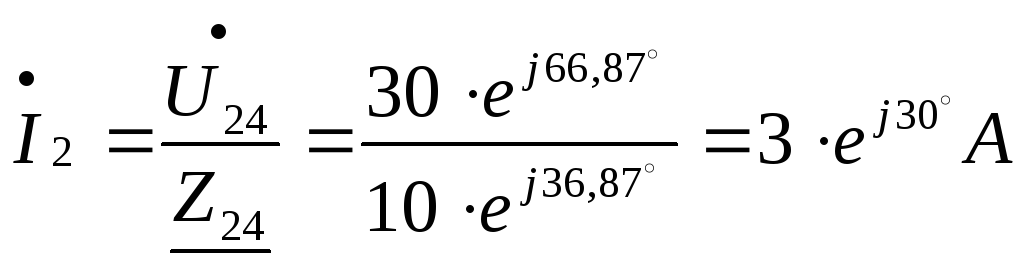
4. Повна потужність кола дорівнює:

Таким чином, повна потужність S=152,8В∙А,

активна потужність Р=151,3Вт,

реактивна потужність Q= – 15,3Вар.

4. Вибираємо масштаб струму m_I=1A/см та масштаб напруги m_V=5В/см і будуємо векторну діаграму в осях комплексних чисел.

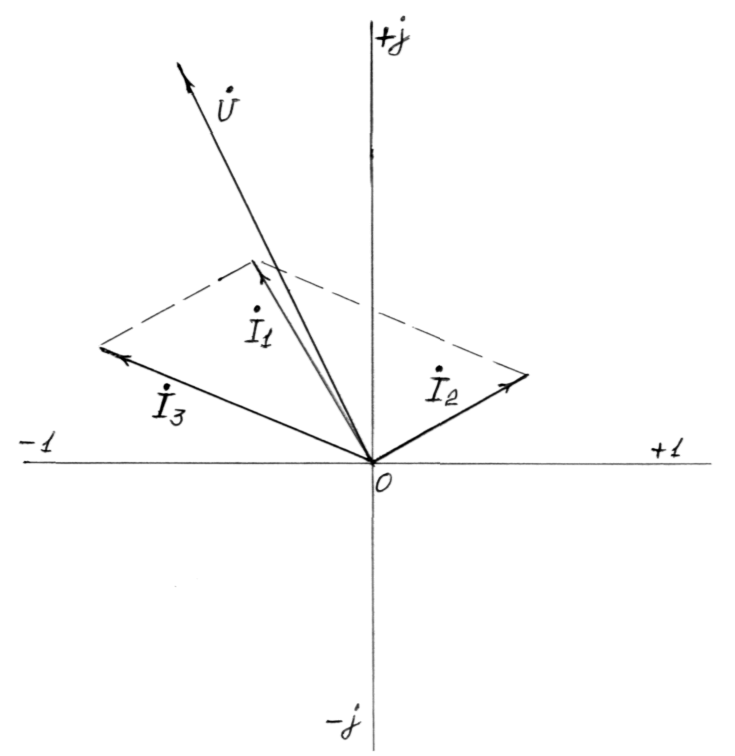
Рис. 9.6.