
- •Общие сведения
- •Краткое содержание
- •Практикум
- •Тема 1. Векторная алгебра.
- •1.1. Понятие вектора и линейные операции над векторами.
- •1.1.1. Понятие вектора.
- •1.1.2. Линейные операции над векторами.
- •Свойства сложения векторов:
- •1.1.3. Понятие линейной зависимости векторов.
- •1.1.4. Линейные комбинации двух векторов.
- •Доказательство.
- •1.1.5. Линейные комбинации трех векторов.
- •Доказательство.
- •1.1.6. Линейная зависимость четырех векторов.
- •1.1.7. Понятие базиса. Аффинные координаты.
- •1.1.8. Проекция вектора на ось.
- •1.1.9. Декартова прямоугольная система координат в пространстве. (дпск)
- •1.2. Скалярное произведение двух векторов.
- •1.2.1. Определение скалярного произведения (сп).
- •1.2.2. Геометрические свойства сп.
- •Доказательство.
- •1.2.3. Алгебраические свойства сп.
- •1.2.4. Выражение скалярного произведения (сп) в декартовых прямоугольных координатах (дпк).
- •1.3. Векторное произведение двух векторов.
- •1.3.1. Правые и левые тройки векторов и системы координат.
- •1.3.2. Векторное произведение двух векторов (вп).
- •1.3.3. Геометрические свойства вп.
- •1.3.4. Алгебраические свойства векторного произведения (вп).
- •1.3.5. Понятие матрицы и определителя второго и третьего порядка.
- •1.3.6. Выражение векторного произведения (вп) в декартовых прямоугольных координатах (дпк).
- •1.3.7. Смешанное произведение трех векторов.
- •1.3.8. Выражение смешанного произведения в декартовых координатах.
- •1.4. Уравнение линии на плоскости.
- •1.4.1.Параметрическое представление линии.
- •1.4.2.Уравнение линии в полярных координатах.
- •1.4.3. Пересечение двух линий.
- •1.4.4. Уравнение поверхности и уравнение линии в пространстве.
- •1.5. Различные виды уравнений прямой на плоскости.
- •1.5.1. Общее уравнение прямой.
- •1.5.2. Уравнение прямой с угловым коэффициентом.
- •1.5.3. Уравнение прямой в отрезках.
- •1.5.4. Каноническое уравнение прямой.
- •1.5.5. Параметрические уравнения прямой.
- •1.5.6. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
- •1.5.7. Нормированное уравнение прямой. Отклонение точки от прямой.
- •1.5.8. Приведение общего уравнения прямой к нормированному виду.
- •Тема 2. Геометрия на плоскости и в пространстве. Общие сведения
- •Краткое содержание
- •Практикум
- •Тема 2. Кривые второго порядка.
- •2.1. Эллипс.
- •2.1.1. Определение эллипса и вывод его канонического уравнения.
- •2.1.2. Исследование формы эллипса.
- •2.1.3. Эксцентриситет и фокальные радиусы эллипса.
- •2.2. Гипербола.
- •2.2.1. Определение гиперболы и вывод ее канонического уравнения.
- •2.2.2. Исследование формы гиперболы.
- •Асимптоты гиперболы
- •Равнобочная гипербола
- •Сопряженная гипербола
- •2.2.3. Эксцентриситет и фокальные радиусы гиперболы.
- •Фокальные радиусы
- •2.3. Парабола.
- •2.3.1. Определение параболы и ее уравнение.
- •2.3.2. Исследование формы параболы.
- •2.4. Общее свойство кривых второго порядка - эллипса, гиперболы и параболы.
- •2.4.1. Директриса эллипса гиперболы и параболы.
- •2.4.2. Полярное уравнение кривой второго порядка.
- •Тема 3. Вещественные и комплексные числа. Общие сведения
- •Краткое содержание
- •Практикум
- •3.1. Плоскость как поверхность первого порядка.
- •3.2. Неполные уравнения плоскости.
- •3.3. Уравнение плоскости в отрезках.
- •3.4. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
- •3.5. Уравнение прямой в пространстве.
- •3.6. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой.
- •3.7. Некоторые дополнительные предложения и примеры.
- •Тема 4. Числовые последовательности. Общие сведения
- •Прямое произведение двух множеств.
- •4.1.2.Вещественные числа и их изображение на числовой оси. Основные свойства рациональных чисел.
- •Измерение отрезков числовой оси.
- •4.1.3. Ограниченные множества вещественных чисел.
- •Теорема 1.
- •4.1.4. Некоторые конкретные множества вещественных чисел.
- •4.2. Теория последовательностей.
- •4.2.1. Понятие числовой последовательности.
- •4.2.2. Бесконечно большие и бесконечно малые последовательности.
- •Примеры.
- •4.2.3. Основные теоремы о бесконечно малых последовательностях.
- •4.2.4. Сходящиеся последовательности. Основные определения.
- •Определение 2.
- •4.2.5. Основные свойства сходящихся последовательностей.
- •4.2.6. Арифметические свойства сходящихся последовательностей.
- •4.2.7. Монотонные последовательности.
- •4.2.8. Число е.
- •4.2.9. Предельный переход в неравенствах.
- •Следствие 1.
- •4.2.10. Подпоследовательности числовых последовательностей.
- •4.2.11. Предельные точки последовательности.
- •4.3. Понятие функции. Предел функции. Непрерывность.
- •4.3.1. Определение функции. Определение 1.
- •4.3.2. Способы задания функций.
- •4.3.3. Монотонные функции.
- •4.3.4. Сложная функция.
- •4.3.5. Обратная функция.
- •4.3.8. Односторонние пределы.
- •4.3.9. Пределы на бесконечности.
1.4. Уравнение линии на плоскости.
Пусть на плоскости заданы декартова прямоугольная система координат Oxy и некоторая линия L. Рассмотрим уравнение, связывающее переменные x и y,
![]() .
(1.1)
.
(1.1)
Определение. Уравнение (1.1) называется уравнением линии L (относительно заданной системы координат), если этому уравнению удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты x и y ни одной точки, не лежащей на линии L.
Т.е. линия L представляет собой геометрическое место точек, координаты которых удовлетворяют уравнению (1.1).
Примеры.
-
Уравнение
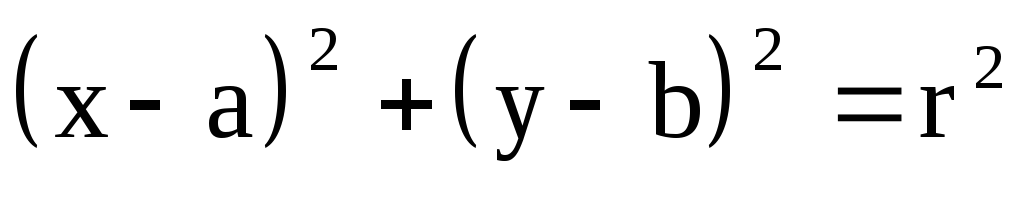 является
уравнением окружности радиуса
является
уравнением окружности радиуса
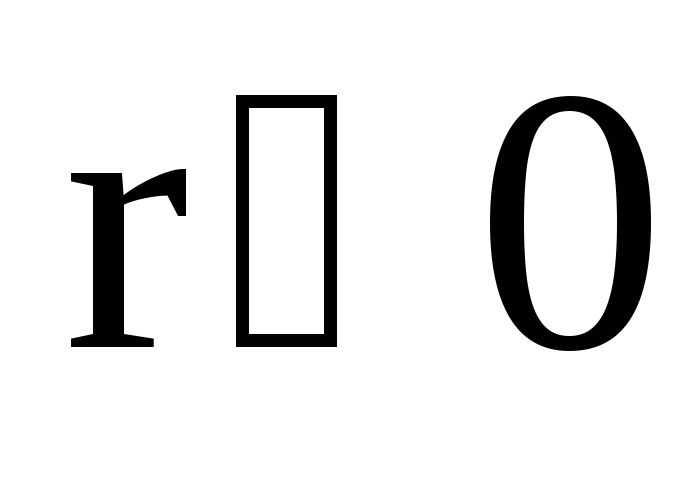 с
центром в точке
с
центром в точке
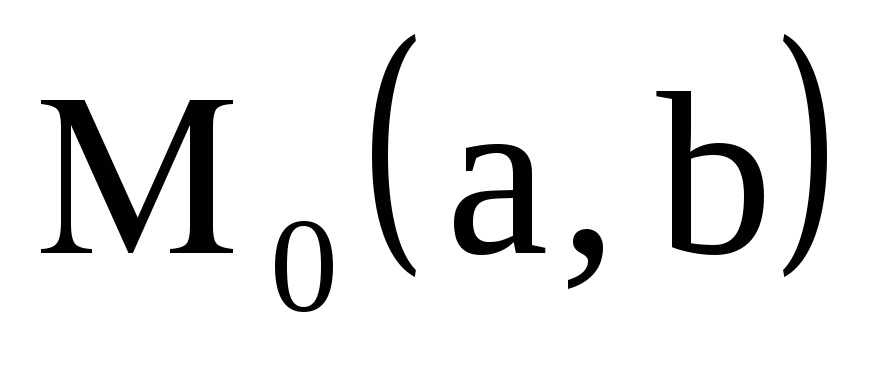 .
. -
Уравнение
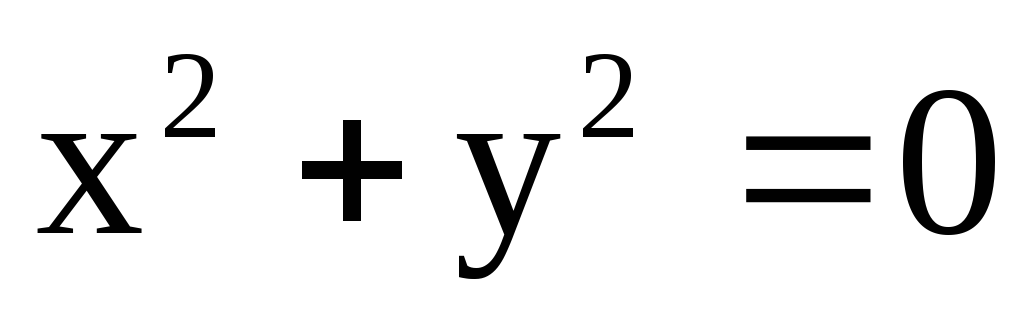 определяет
на плоскости Oxy только одну точку (0,0).
определяет
на плоскости Oxy только одну точку (0,0). -
Уравнение
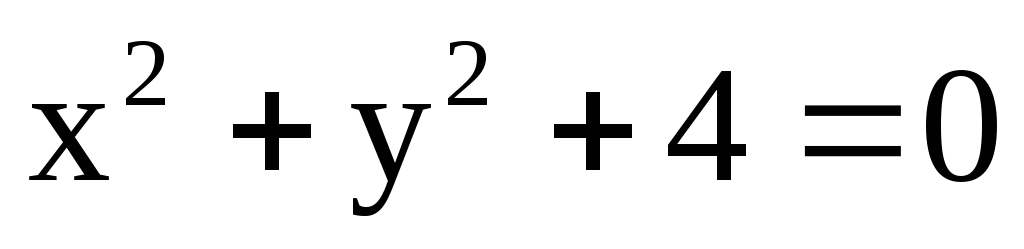 вообще
не определяет никакого геометрического
образа.
вообще
не определяет никакого геометрического
образа.
1.4.1.Параметрическое представление линии.
Для аналитического представления линии L возможно выражать координаты x и y точек этой линии при помощи параметра t :
![]() ,
(2.1.)
,
(2.1.)
где функции
![]() непрерывны
по параметру t в области
непрерывны
по параметру t в области![]() изменения
этого параметра. Исключение из двух
уравнений (2.1) параметра t приводит к
уравнению вида (1.1).
изменения
этого параметра. Исключение из двух
уравнений (2.1) параметра t приводит к
уравнению вида (1.1).
Пример. Найдем
параметрические уравнения окружности
радиуса
![]() с
центром в начале координат.
с
центром в начале координат.
|
|
Пусть
|
Эти уравнения представляют
собой параметрические уравнения нашей
окружности. Чтобы точка
![]() один
раз обошла окружность, t должно изменяться
в пределах:
один
раз обошла окружность, t должно изменяться
в пределах:![]() .
Для исключения параметра t из уравнения
(2.2) нужно возвести в квадрат и сложить
уравнения (2.2); получим
.
Для исключения параметра t из уравнения
(2.2) нужно возвести в квадрат и сложить
уравнения (2.2); получим
![]() .
.
1.4.2.Уравнение линии в полярных координатах.
Введем на плоскости полярные координаты. Выберем на плоскости точку O (полюс) и выходящий из нее луч Ox; укажем единицу масштаба.

Полярными координатами
точки M называются
два числа:
![]() (полярный
радиус) равное расстоянию точки M от
полюса O и
(полярный
радиус) равное расстоянию точки M от
полюса O и
![]() (полярный
угол)- угол, на который нужно повернуть
против часовой стрелки луч Ox до совмещения
с лучом OM. Точку M обозначают символом
(полярный
угол)- угол, на который нужно повернуть
против часовой стрелки луч Ox до совмещения
с лучом OM. Точку M обозначают символом
![]() и
обычно считают, что
и
обычно считают, что
![]() .
.
Если начало декартовой
прямоугольной системы находится в
полюсе, а ось абсцисс совпадает с полярной
осью, то очевидна связь между полярными
координатами точки
![]() и
ее декартовыми координатами
и
ее декартовыми координатами
![]() :
:
![]() .
(3.1)
.
(3.1)
Возводя эти уравнения
в квадрат и складывая их, получим
![]() .
Разделив одно на другое, получим, что
.
Разделив одно на другое, получим, что
![]() ,
а также, используя знаки x и y, определим
четверть, в которой находится точка M.
Т.е., зная декартовы координаты точки x
и y, можно найти ее полярные координаты.
,
а также, используя знаки x и y, определим
четверть, в которой находится точка M.
Т.е., зная декартовы координаты точки x
и y, можно найти ее полярные координаты.
Если
![]() представляет
собой уравнение линии L в декартовой
прямоугольной системе координат Oxy, то
достаточно подставить вместо x и y их
выражения в полярных координатах (3.1):
получим
представляет
собой уравнение линии L в декартовой
прямоугольной системе координат Oxy, то
достаточно подставить вместо x и y их
выражения в полярных координатах (3.1):
получим![]() ,
где использовали обозначение
,
где использовали обозначение
![]() .
.
1.4.3. Пересечение двух линий.
Задача о нахождении
точек пересечения двух линий
![]() ,
заданных уравнениями
,
заданных уравнениями
![]() ,
состоит в нахождении координат точек,
удовлетворяющих каждому из этих
уравнений.
,
состоит в нахождении координат точек,
удовлетворяющих каждому из этих
уравнений.
Т.е. нужно решить систему уравнений
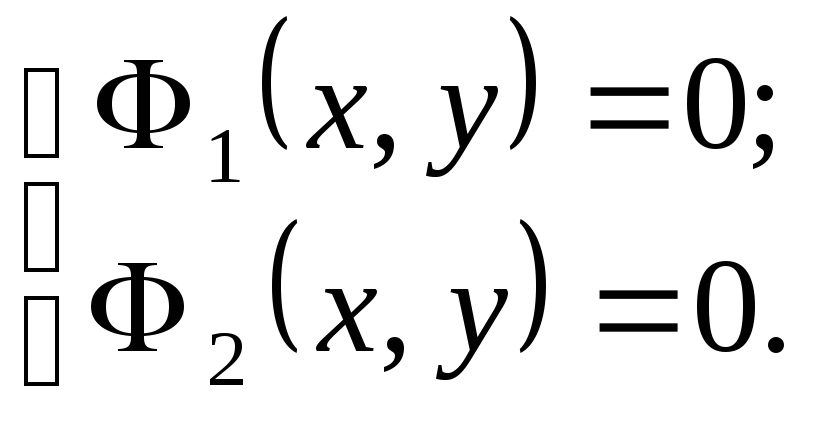
Если эта система не
имеет решений, то линии
![]() не
пересекаются.
не
пересекаются.
Пример. Найти
точки пересечения окружностей
![]() .
.
Решаем систему уравнений
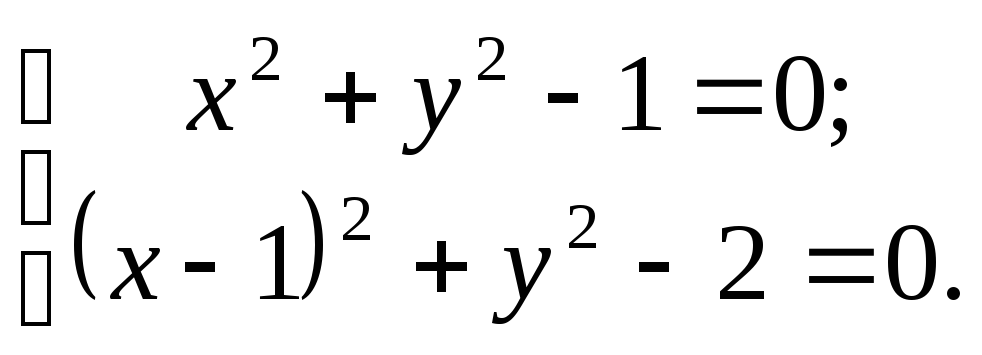
Вычитая из первого уравнения второе, получим
![]()
Отсюда найдем, что
![]() .
Мы получили две точки пересечения
.
Мы получили две точки пересечения
![]() .
.

