1.1.6. Линейная зависимость четырех векторов.

 

Теорема. Любые четыре вектора линейно зависимы.

 

Доказательство. Исключим случай, когда какая-нибудь тройка из данных четырех векторов компланарна, т.к. тогда указанная тройка линейно зависима и, следовательно, все четыре вектора линейно зависимы.

 

Осталось рассмотреть случай, когда среди четырех векторов никакая тройка векторов не компланарна.

Приведем все четыре вектора к общему началу О и проведем через конец D вектораd плоскости, параллельные плоскостям, определяемым парами векторов.

 

. . Следовательно, .

 

Или , ч.т.д.

 

Следствие. Каковы бы ни были некомпланарные векторы , для любого вектора найдутся такие вещественные числа   и , что справедливо равенство

 

.

 

 

1.1.7. Понятие базиса. Аффинные координаты.

 

Определение 1. Три линейно независимых вектора образуют в пространстве базис, если любой вектор может быть представлен в виде линейной комбинации векторов .

 

Аналогично определяется базис на плоскости .

 

Определение 2. Два лежащих в плоскости  линейно независимых вектора образуют на этой плоскости базис, если любой лежащий в этой плоскости вектор может быть представлен в виде линейной комбинации векторов .

Имеют место следующие фундаментальные утверждения:

 

1. любая тройка некомпланарных векторов 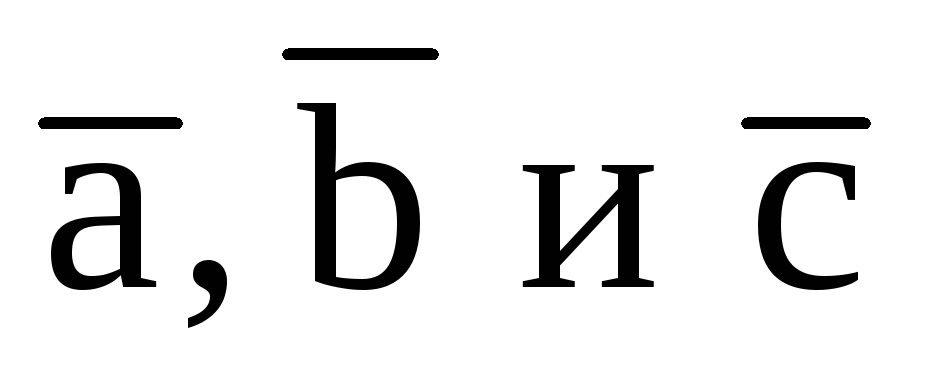образует базис в пространстве;

2. любая пара лежащих в данной плоскости неколлинеарных векторов образует базис на этой плоскости.

 

Теорема. Каждый вектор может быть единственным способом разложен по базису :

 

.

 

Числа    называются координатами вектора относительно базиса .

 

Доказательство. Пусть таких разложений два:

 

и .

 

Вычитая почленно получаем

 

.

 

В силу линейной независимости базисных векторов :

 

.

 

Единственность разложения по базису доказана.

 

Теорема. При сложении двух векторов их координаты складываются. При умножении вектора на любое число  все его координаты умножаются на это число.

 

Доказательство. Пусть .

 

Тогда в силу свойств линейных операций

 

.

.

 

В силу единственности разложения по базису теорема доказана.

 

Аффинные координаты в пространстве определяются заданием базиса и некоторой точки О, называемой началом координат.

 

Аффинными координатами любой точки М называются координаты вектора (относительно базиса ).

Свойства базиса и понятие аффинных координат на плоскости аналогичны случаю пространства.

 

1.1.8. Проекция вектора на ось.

 

Определение. Проекцией вектора на ось U называется величина направленного отрезка оси U, где - основания перпендикуляров, опущенных на ось U из точек A и B соответственно.

 

Теорема 1.8. Проекция вектора на ось U равна длине вектора , умноженной на косинус  угла наклона вектора к оси U.

 

Доказательство.

Обозначим через V ось, проходящую через начало A вектора и имеющую тоже направление, что и ось U, и пусть C- проекция B на ось V.

 

BAC=, = AC.

Т.к. по определению пр_и, то пр_и.

Но cos=cos. Следовательно пр_и, ч.т.д.