Асимптоты гиперболы

 

Пусть Г - какая-нибудь линия, М - переменная точка на ней, а - некоторая прямая. Если возможно такое движение точки М по линии Г, что:

1. точка М уходит в бесконечность;

2. при этом расстояние от точки М до прямой а стремится к нулю, -

то говорят, что линия Г ассимптотически приближается к прямой а. Прямая а в таком случае называется асимптотой линии Г.

Асимптотами гиперболы называются прямые, имеющие уравнения:

 

и . (3)

 

Эти прямые являются диагоналями основного прямоугольника. Построим гиперболу и рассмотрим какую-нибудь точку М(х;у), лежащую на гиперболе в первом квадранте.

 

Выясним, как в первом квадранте по мере возрастания х будет изменяться расстояние от точки М гиперболы до асимптоты . Обозначим через N точку асимптоты с абсциссой х: N(x;Y), где Y=. Тогда

 

(4)

 

Так как а  х, то в скобках первое слагаемое всегда больше второго, следовательно, Y-y>0, а это означает, что при одной и той же абсциссе точка гиперболы лежит под соответствующей точкой асимптоты.

 

Преобразовав неравенство (4):

 

, (5)

 

убеждаемся, что длина отрезка MN по мере возрастания х уменьшается, и когда х неограниченно растет, MN стремится к нулю. Так как MN больше расстояния МК от точки M до асимптоты, то при этом МК и подавно стремится к нулю.

Аналогичное рассуждение можно провести в любом квадранте.

Итак, прямые в смысле определения асимптот к графику функции являются асимптотами гиперболы

 

.

При построении гиперболы обычно строят основной прямоугольник и проводят асимптоты, так как они позволяют точнее вычерчивать гиперболу.

 

Равнобочная гипербола

Возьмем каноническое уравнение гиперболы

 

.

 

В случае, когда а=b, уравнение гиперболы имеет вид

или

 

х² - у² = а². (6)

 

Гипербола, у которой полуоси а и b равны, называется равнобочной гиперболой. Уравнение (6) называется уравнением равнобочной гиперболы. Так как основной прямоугольник этой гиперболы является квадратом, то асимптоты равнобочной гиперболы будут перпендикулярны друг другу. (Рис. 5)

 

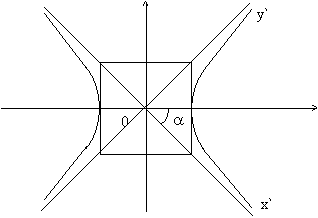
Рис. 5

 

 

Сопряженная гипербола

Рассмотрим уравнение

. (7)

Представим уравнение (7) в следующем виде:

. (8)

Очевидно, что уравнение (8) представляет собой уравнение гиперболы, у которой действительной осью является ось ординат, а мнимой - ось абсцисс.

 

Построим основной прямоугольник, проведем асимптоты и построим гиперболу (7). Далее в той же системе координат построим (пунктиром) (Рис. 6) гиперболу

 

 

Рис. 6

Очевидно, что гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными.

Выведем теперь уравнение гиперболы, асимптотами которой служат оси координат. Возьмем уравнение равнобочной гиперболы х² - у² = а² и рассмотрим уравнение этой гиперболы в новой системе координат Х`OY`, полученной из старой поворотом осей координат на угол =(Рис. 2).

 

Используя для этого формулы поворота осей координат:

 

х = х`cos - y`sin;

y = x`sin + y`cos,

 

подставим значения х, у в уравнение гиперболы:

 

х² - у² = а².

 

Получим:

 

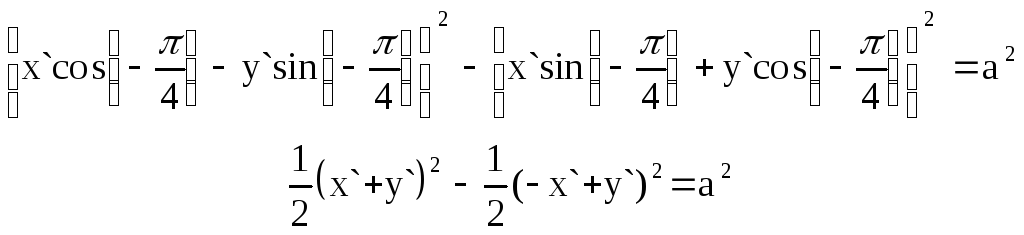
. (9)

 

Обозначая , получим х`y`=c.

Уравнение равнобочной гиперболы, для которой координатные оси ОХ и OY являются асимптотами, будет иметь вид:

ху = с

или

.