2.2. Гипербола.

 

2.2.1. Определение гиперболы и вывод ее канонического уравнения.

 

Гиперболой называется геометрическое место точек на плоскости, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная; указанная разность берется по абсолютному значению. Кроме того, требуется, чтобы разность была меньше расстояния между фокусами и отлична от нуля. Фокусы гиперболы обозначим через F₁ и F₂, а расстояние между ними - через 2с.

 

Рис.3

Для вывода уравнения гиперболы возьмем систему координат XOY так, чтобы фокусы гиперболы F1 и F2 лежали на оси абсцисс, а начало координат делило отрезок F1F2 (F1F2=2c) пополам. Тогда координаты фокуса F1 будут (с;0), а фокуса F2 - числа (-с;0).

Возьмем точку M(x;y), лежащую на гиперболе, и проведем отрезки MF₁ и MF₂. Длину отрезка MF₁ обозначим r₁, а длину отрезка MF₂ - через r₂:

 

MF₁ = r₁; MF₂ = r_2.

 

Числа r₁ и r₂ называются фокальными радиусами точки М гиперболы. Обозначив разность фокальных радиусов через 2а, имеем 2а<2c или а<c.

 

На основании определения гиперболы как геометрического места точек на плоскости, можно утверждать, что для всех точек гиперболы, и только для них, должно выполняться равенство:

 

r₁ - r₂ =  2a. (1)

 

По формуле расстояния между двумя точками имеем:

 

Подставляя найденные значения r₁ и r₂ в уравнение (1), получим:

 

. (2)

 

Уравнение (2) является уравнением гиперболы. Приведем уравнение (2) к более удобному виду:

 

Возведем обе части в квадрат:

 

или

 

. (3)

 

Возводя в квадрат обе части этого равенства, найдем:

 

то есть

 

(4)

 

Так как по условию а<c, то с² - а² >0, обозначая с² - а² = b² (3). Подставив в равенство (4) b² = с² - а², а затем деля все его члены на а²b², получим:

 

b²x² - a²y² = a²b²

 

то есть

 

(6)

 

Уравнению (6) будут удовлетворять координаты каждой точки, лежащей на гиперболе. Можно показать, что координаты точек, не принадлежащих гиперболе, уравнению (6) не удовлетворяют. Следовательно, уравнение (6) является уравнением рассматриваемой гиперболы. Уравнение (6) называется каноническим уравнением гиперболы.

 

 

2.2.2. Исследование формы гиперболы.

 

Займемся исследованием гиперболы, определяемой уравнением

 

Прежде всего заметим, что в уравнение гиперболы обе координаты входят только в четных степенях. Следовательно, если некоторая точка М₀(х₀;у₀) лежит на гиперболе, то на гиперболе будут лежать также точки М₁(х₀;-у₀); М₂(-х₀;у₀); М₃(-х₀;-у₀). Отсюда следует, что гипербола является кривой, симметричной относительно обеих координатных осей и начала координат. Это позволяет изучение формы гиперболы ограничить первым квадрантом, а затем получившуюся кривую с помощью зеркального отображения построить во всех четырех квадрантах.

 

В случае канонического задания гиперболы координатные оси являются осями симметрии гиперболы. Таким образом, гипербола, как и эллипс, - центральная кривая.

 

От начала координат на оси абсцисс вправо и влево отложим отрезки, длины которых равны а, и построим точки A₁(a;0) и А₂(-а;0), а на оси ординат вверх и вниз отложим отрезки длины b и построим точки В₁(0;b) и B₂(0;-b). Затем через точки А₁, А₂, В₁, В₂ проведем прямые, параллельные координатным осям, до их взаимного пересечения и таким образом построим прямоугольник (Рис. 4), который назовем основным прямоугольником гиперболы.

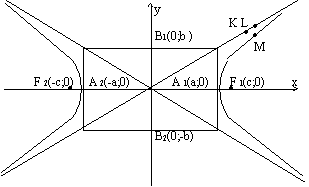
 Рис. 4

Раствором циркуля, равным расстоянию А₁В₁, из начала координат как из центра, сделаем засечки на оси абсцисс. При этом мы найдем точки F₁ и F₂. Действительно, из прямоугольного треугольника ОА₁В₁: ОА₁=а, ОВ₁=b. Следовательно, на основании равенства

 

a² + b² = c², то есть В₁А₁=с.

 

Определим теперь у из канонического уравнения гиперболы :

 

. (1)

 

Так как исследование гиперболы будет вестись в первом квадранте, то в этом равенстве надо перед корнем взять знак плюс:

 

(2)

 

и рассматривать х  0.

1. Если 0  х<a, то у получает мнимые значения. Следовательно, точек гиперболы с абсциссами х, 0  х<a, не существует.

2. Если х=а, то у=0. Следовательно, точка А₁(а;0) принадлежит гиперболе.

3. Если х>а, то у>0, причем при возрастании х возрастает и у.

Когда х неограниченно возрастает, у также неограниченно возрастает. Следовательно, при неограниченном возрастании х ветвь гиперболы уходит в бесконечность.

 

Отсюда следует, что гипербола представляет собой кривую, состоящую из двух бесконечных ветвей (для правой ветви r₁ - r₂ = 2a, для левой r₁ - r₂ = + 2a) с двумя взаимно перпендикулярными осями симметрии, причем ни одной точки гиперболы не находится внутри основного прямоугольника.

 

Отрезок А₂А₁ и его длина 2а называются действительной осью гиперболы, отрезок ОА₁ и его длина а называются действительной полуосью гиперболы. Отрезок В₂В₁ и его длина 2b называются мнимой осью гиперболы; отрезок ОВ₁ и его длина b называются мнимой полуосью гиперболы. Длина 2с отрезка F₂F₁ называется фокусным расстоянием. Точки пересечения гиперболы с действительной осью А₁ и А₂ называются вершинами гиперболы.