§ 3. Неопределенный интеграл

В интеграле 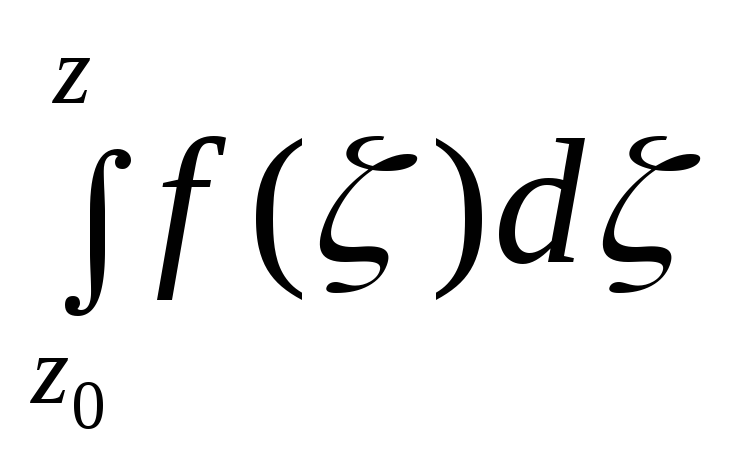зафиксируем нижний придел z₀ интегрирования и будем рассматривать интеграл как функцию верхнего предела 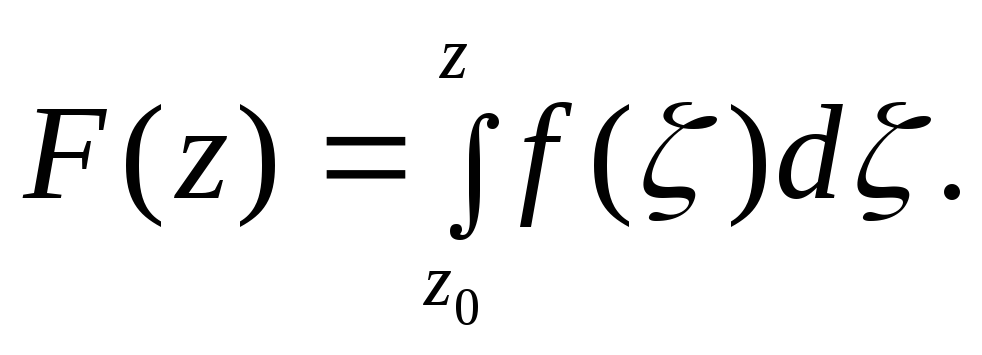Тогда для функции f (z) можно доказать теорему.

Теорема.

Если функция f (z) непрерывна в односвязной области D и интеграл

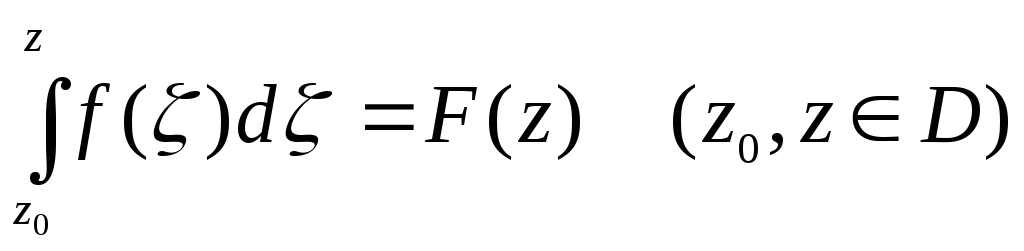(4.10)

не зависит от пути интегрирования, то однозначная в области D функция f (z) аналитична в D, причем

Доказательство. По определению производной и на основании свойств интеграла можем записать

Рис. 4.4

где z – произвольная точка D, (рис. 4.4). В силу непрерывности функции f(z)

в точке z имеем

где при .

Учитывая это, получим:

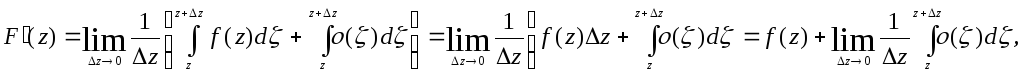
но

при .

(путь интегрирования от точки z до точки считаем прямолинейным).

Отсюда и, следовательно,

Функция Ф(z) называется первообразной для функции f(z) в некоторой области D, если (Ф(z))′= для .

Из доказанной теоремы следует, что 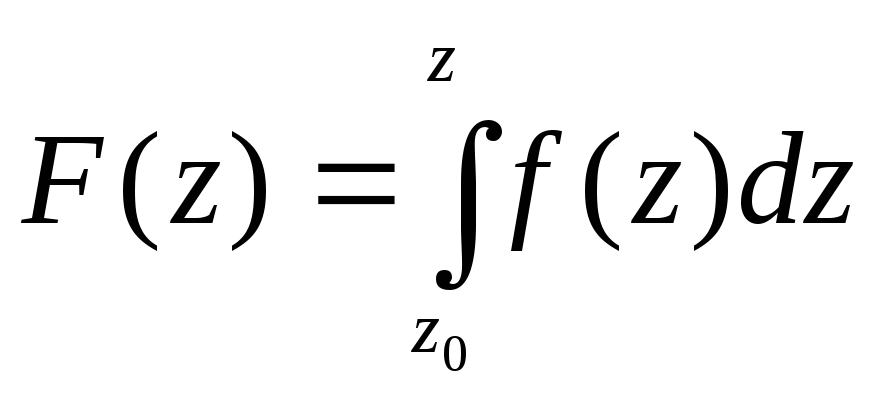является первообразной для функции f(z). Можно легко доказать следующую теорему.

Теорема.

Любые две первообразные одной и той же функции отличаются друг от друга не более, чем на постоянное слагаемое.

Доказательство предоставляется провести самостоятельно.

На основании этой теоремы можно записать:

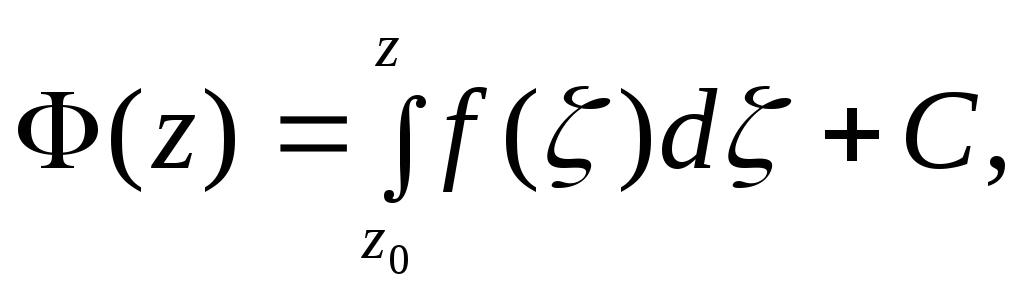где Ф(z) – любая первообразная функция

При следовательно,

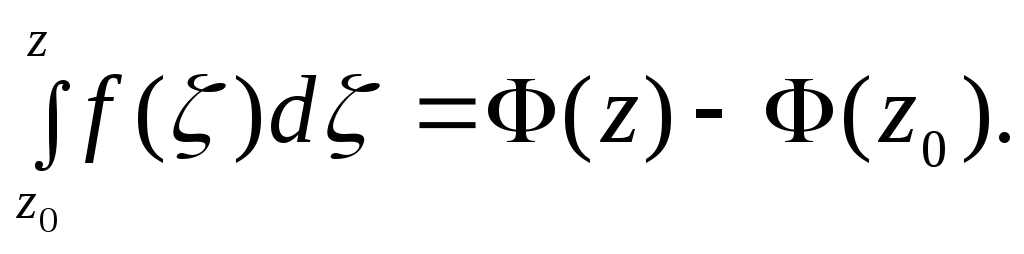(4.11)

Мы получили формулу, аналогичную формуле Ньютона-Лейбница для вычисления определенного интеграла функции действительного переменного.

Пример.

Рассмотрим . Подынтегральная функция аналитична в любой односвязной области D комплексной плоскости, не содержащей току z = 0, например, в области . В этой области является первообразной для функции Поэтому Предположим теперь, что линия, соединяющая точку z = 1 с точкой z, пересекает отрицательную

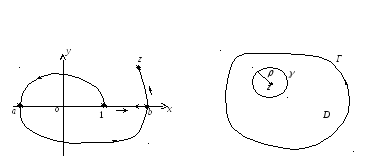
Рис.4.5 Рис.4.6

действительную ось (рис. 4.5). В этом случае, учитывая пример 1 § 1, будем иметь

Если путь интегрирования совершает k оборотов вокруг точки z = 0, то (знак определяется направлением движения по кривой). Таким образом, мы получаем ту или иную ветвь многозначной функции Lnz . Можно написать .

§ 4. Интегральная формула Коши и ее приложения.

Интегральная формула Коши.

Пусть Г кусочно-гладкая граница односвязной области D и f(z) – функция, аналитическая в области D и непрерывная в замкнутой области

Рассмотрим произвольную точку :

Функция переменной аналитична всюду в области D за исключением точки .

Опишем окружность радиуса р с центром в точке z, принадлежащую области D (рис. 4.6).

Так как функция f(z) аналитична в двухсвязной области ограниченной Г и , и непрерывна на ее границе , то по теореме Коши , т.е. интеграл не зависит от радиуса р окружности. Так как существует , то доопределив функцию в точке , положив , будем иметь функцию , непрерывную в области D, а значит и ограниченную в ней: .

Учитывая это, получим:

В силу произвольности р и постоянства M

т.е. или

отсюда получаем интегральную формулу Коши:

т.е. значение функции f(z), аналитической в области D непрерывна в , можно выразить чрез ее значения на границе области Г.

Пример 1. Вычислить интеграл

Т. к. аналитична в замкнутой области, ограниченной окружностью, то по интегральной формуле Коши имеем:

Если рассмотреть этот же интеграл, но в качестве контура взять

окружность то

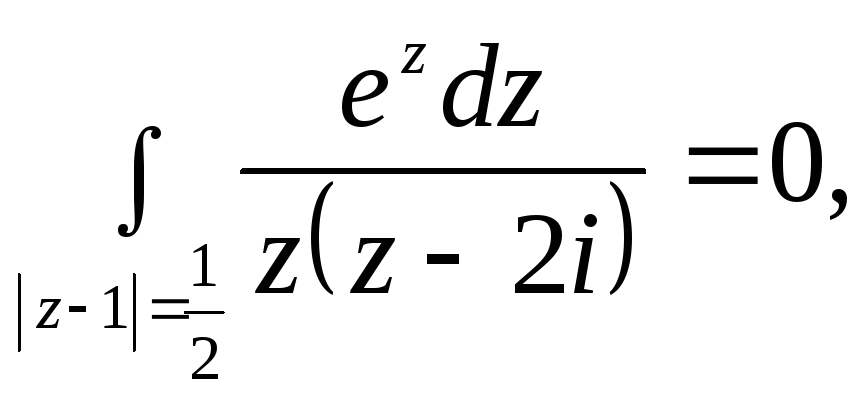
т. к. подынтегральная функция аналитична всюду в замкнутой области, ограниченной окружностью

Правую часть интегральной формулы Коши называют интегралом Коши.

Следствие 1. В частном случае, если кривая Г является окружностью с центром в точке z радиуса R, т. е. мы имеем и тогда

т. е. f (z) есть среднее арифметическое значение f () на окружности центром z.

Интегральная формула Коши справедлива и для многосвязной области. Действительно, пусть D многосвязная область, ограниченная контуром и функция f (z) аналитична в D и непрерывна .

Рис. 4.7.

Рассмотрим произвольную точку . Окружим точку z окружностью C_R, так, чтобы область, ограниченная окружностью C_R , вместе с самой окружностью полностью принадлежала D (рис. 4.7). Тогда функция удовлетворяет условиям теоремы Коши в (m + 2)-связной области ограниченной контуром и следовательно,

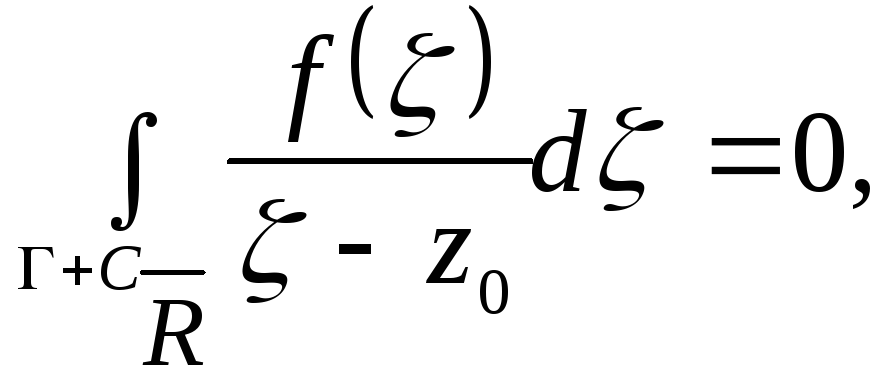или

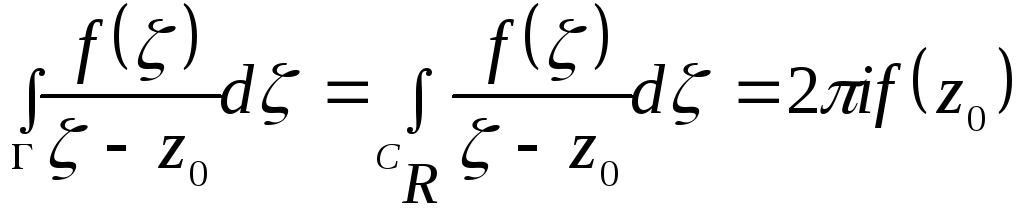
на основании доказанной выше теоремы.

Отсюда

Неограниченная дифференцируемость аналитической

функции

Используя представление функции интегралом Коши (6.6), можно показать, что аналитическая в области в функция дифференцируема в точках области D сколько угодно раз.

Теорема. Если функция f (z) аналитична в области D и непрерывна в области , то она обладает в области D производными всех порядков, причем n-ая производная представляется формулой

(6.7)

где Г - граница области D.

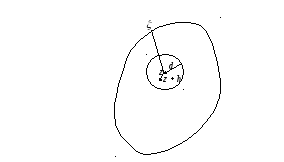
Рис. 4.8

Доказательство. Пусть z – произвольная точка области D (Pис.4.8). На основании интегральной формулы Коши имеем

Оценим разность

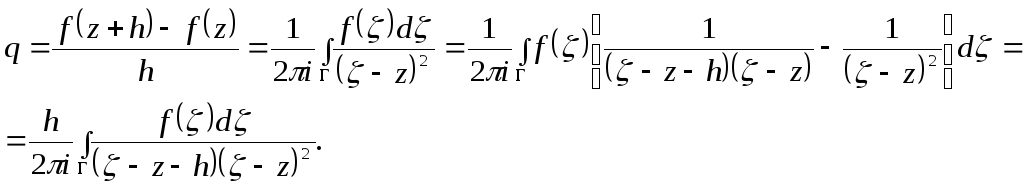
Из непрерывности f (z) на замкнутом множестве Г следует ограниченность f (z) на Г, т.е. существует М >0 такое, что < М для С другой стороны поэтому существует такое, что . Тогда для имеем

Отсюда

Где l - длина Г. Т. к. M, l, d не зависят от L, то при . Следовательно,

Мы доказали формулу (6.7) для n = 1.

Для любого n > 1 формула доказывается индукцией по n.

Пример 2. Вычислить К этому интегралу можно применить формулу (6.7), тогда

Замечание: неравенства Коши.

Обозначим через М максимум в области D, через R расстояние от точки z до границы и через l длину границы Г, тогда из интегральной формулы для n-ой производной имеем:

В частности, если (z) аналитична в круге , то принимая в качестве D этот круг, будем иметь:

(n = 0, 1, 2…). (6.8)

Эти неравенства называют неравенствами Коши.