§ 2. Теорема Коши

Теорема Коши.

Если функция f(z) аналитична в односвязной области D и Г - произвольная замкнутая кусочно-гладкая кривая Жордана в D, то

. (4.9)

Мы докажем эту теорему при дополнительном предположении, что производная функции непрерывна в D.

Пусть тогда

В силу предположения, функции u (х, у) и v(х, у) непрерывны в области D вместе со своими частными производными, а потому для них справедлива формула Грина:

где D_Г – область, ограниченная контуром Г. Равенство нулю двойных интегралов следует из условий Коши-Римана, выполняющихся для аналитической в D функции f(z). А из полученных равенств получаем: Теорема доказана.

Теорема Коши доказана нами для односвязной области, но ее можно обобщить и на случай многосвязной области.

Теорема Коши (для многосвязной области)

Пусть f(z) - аналитическая в области D функция. И пусть замкнутые кусочно-гладкие кривые Жордана, лежащие внутри области D, причем лежат внутри и во внешности друг друга, и многосвязная (n + 1 – связная) область G, ограниченная кривыми , , лежит внутри области D.

Обозначим через Г сложный контур, состоящий из контура (проходимого в положительно направлении) и контуров , , (проходимых в отрицательном направлении). (См. рис. 4.2)

Рис. 4.2

Тогда справедлива формула: , где

Это равенство можно переписать в такой форме:

Доказательство. Соединим последовательно контуры с помощью криволинейных отрезков, лежащих внутри D. Тогда вместо (n + 1)-го замкнутого контура, будем иметь два контура Г₁ и Г₂, ограничивающих соответственно две области D₁ и D₂. При этом 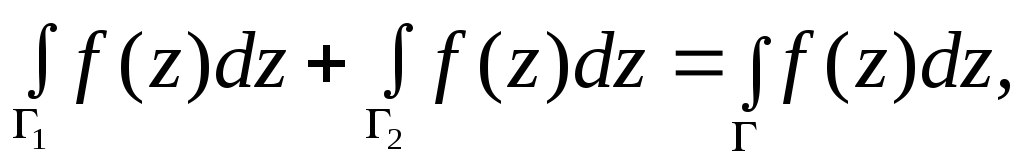так как каждый вспомогательный отрезок, соединяющий и (i = 0, 1, …, n - 1), проходится дважды в разных направлениях. Каждая из областей D₁ и D₂, является односвязной и принадлежит вместе со своей границей области D.

Поэтому для каждой из них справедлива теорема Коши для односвязной области:

;

следовательно,

,

что и требовалось доказать.

Пример.

Вычислить интеграл по замкнутому контуру Г.

1. Пусть точка z = а не принадлежит области, ограниченной Г, тогда по

теореме Коши

2. Предположим, что точка z = а принадлежит области ограниченной

контуром Г. (См. рис. 4.3).

Рис. 4.3

В этом случае теорема Коши не применима. Возьмем в качестве нового контура окружность C_R достаточно малого радиуса R с центром в точке a такую, чтобы она лежала внутри контура Г.

Так как в двухсвязной области, ограниченной C_R и Г, применима теорема Коши, то

или

(последний интеграл вычислен в примере §1).

Замечание. Из теоремы Коши следует, что интеграл от функции f(z), аналитической в односвязной области D, не зависит от пути интегрирования, а зависит лишь от его начала и конца, т.е. , где А и В – соответственно начало и конец кривой, принадлежащей области D аналитичности функции f (z).