
- •Глава 4 интегрирование функций комплексного переменного
- •§ 1. Определение интеграла от функции комплексного
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •Теорема Лиувилля
- •Операционное исчисление
- •§ 1. Оригинал и изображение
- •§ 2. Свойства преобразования Лапласа
- •§ 3. Изображение функции Дирака
- •§ 4. Теорема обращения
- •§ 4. Теорема разложения
Глава 4 интегрирование функций комплексного переменного
§ 1. Определение интеграла от функции комплексного
Переменного и его свойства
Определение интеграла
Пусть задана некоторая ориентированная
непрерывная кривая
![]() и на ней однозначная функция комплексного
переменного
и на ней однозначная функция комплексного
переменного
![]() .
Разобьем кривую
.
Разобьем кривую
![]() произвольно на
произвольно на
![]() элементарных дуг точками
элементарных дуг точками
![]() ,
записанными в порядке их следования на
кривой (точки
,
записанными в порядке их следования на
кривой (точки![]() и
и
![]() -
начало и конец кривой
-
начало и конец кривой
![]() соответственно), и на каждой из дуг
соответственно), и на каждой из дуг
![]() также произвольно возьмем по точке
также произвольно возьмем по точке
![]() .
(См. рис. (4.1)). Обозначим
.
(См. рис. (4.1)). Обозначим
![]() .
.
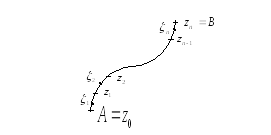
Рис. 4.1
Назовем интегралом
![]() вдоль
вдоль
![]() предел
предел
![]() ,
(4.1)
,
(4.1)
если он существует и не зависит ни от
способа разбиения кривой
![]() ,
ни от выбора точек
,
ни от выбора точек
![]() .
.
Вопрос о существовании комплексного интеграла (4.1) сводится к вопросу о существовании криволинейного действительного интеграла.
Действительно, положив
![]() ,
,
![]()
получим
![]() .
Замечаем, что суммы в правой части
полученного равенства представляют
собой интегральные суммы криволинейных
интегралов
.
Замечаем, что суммы в правой части
полученного равенства представляют
собой интегральные суммы криволинейных
интегралов
![]() и
и
![]() соответственно. А поэтому, как следует
из теоремы о существовании криволинейного
интеграла, для существования интеграла
(4.1) достаточно, чтобы кривая
соответственно. А поэтому, как следует
из теоремы о существовании криволинейного
интеграла, для существования интеграла
(4.1) достаточно, чтобы кривая
![]() была кусочно-гладкой, а функции
была кусочно-гладкой, а функции
![]() и
и
![]() кусочно-непрерывными функциями
действительных переменных, или что-то
же самое, чтобы функция
кусочно-непрерывными функциями
действительных переменных, или что-то
же самое, чтобы функция
![]() была
непрерывной на
была
непрерывной на
![]() .
Итак, интеграл (4.1) можно связать с
криволинейными интегралами формулой
.
Итак, интеграл (4.1) можно связать с
криволинейными интегралами формулой
![]() .
(4.2)
.
(4.2)
Примеры:
1. Пусть
![]() .
Тогда интегральная сумма
.
Тогда интегральная сумма
![]()
следовательно,
![]() .
.
В частности, если
![]() - замкнутая кривая
- замкнутая кривая
![]() ,
то
,
то
![]() .
.
2. Пусть
![]() ,тогда,
полагая
,тогда,
полагая
![]() ,
получим интегральные суммы
,
получим интегральные суммы
![]() ,
если же положить
,
если же положить
![]() ,
то интегральные суммы примут вид
,
то интегральные суммы примут вид
![]() .
.
Так как эти суммы имеют один и тот же
предел, то их среднее арифметическое
имеет тот же предел
![]() ,
следовательно
,
следовательно
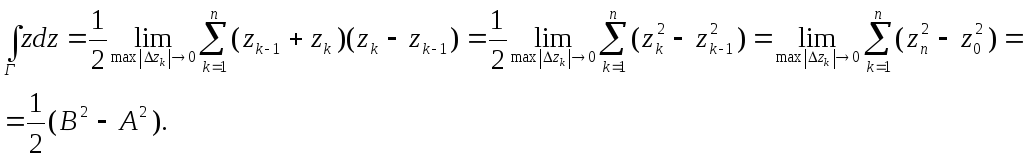
Свойства интеграла функции комплексного переменного
1.
![]() .
(4.3)
.
(4.3)
2.
![]() ,
(4.4)
,
(4.4)
где
![]() обозначает кривую, составленную из дуг
обозначает кривую, составленную из дуг
![]() и
и
![]() ,так
что конец
,так
что конец
![]() совпадает с началом
совпадает с началом
![]() .
.
3.
![]() ,
(4.5)
,
(4.5)
где
![]() -
комплексная постоянная.
-
комплексная постоянная.
4.
![]() .
(4.6)
.
(4.6)
Свойства 1-4 могут быть получены из определения интеграла или из формулы (4.2)
5.![]() (4.7)
(4.7)
где
![]() - длина кривой
- длина кривой
![]() ,
отсчитываемая от начала до произвольной
ее точки.
,
отсчитываемая от начала до произвольной
ее точки.
Интеграл
![]() часто записывают также как
часто записывают также как
![]() .
Действительно, в силу неравенства
.
Действительно, в силу неравенства
![]()
для модуля интегральной суммы можно записать:
![]() ,
,
но
![]() длины
длины
![]() ,
следовательно,
,
следовательно,
![]() .
.
Переходя к пределу в последнем
неравенстве при условии
![]() ,
получаем формулу (4.7). В частности, если
,
получаем формулу (4.7). В частности, если
![]() для
для
![]() ,
из формулы (4.7) следует
,
из формулы (4.7) следует
![]() для
для
![]() .
.
6. Пусть
![]() - действительный параметр) – уравнение
гладкой кривой
- действительный параметр) – уравнение
гладкой кривой
![]() ,
тогда
,
тогда
![]() .
(4.8)
.
(4.8)
Действительно, на основании формулы (4.4) способ вычисления криволинейного интеграла дает
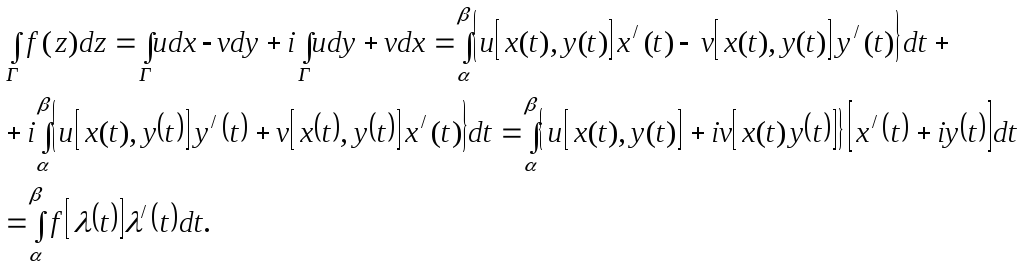
Пример.
Вычислить интеграл
![]() ,
причем окружность проходится против
часовой стрелки. Уравнение окружности
,
причем окружность проходится против
часовой стрелки. Уравнение окружности
![]() ,
где
,
где
![]() .
Применяя формулу (4.4) имеем
.
Применяя формулу (4.4) имеем
![]() .
.
Замечание. Пусть
![]() - замкнутая кусочно-гладкая кривая
Жордана. Условимся под записью
- замкнутая кусочно-гладкая кривая
Жордана. Условимся под записью
![]() понимать интеграл вдоль контура Г
в положительном направлении (т.е. когда
область ограниченная кривой Г ,
остается слева при движении по Г).
Когда интегрирование по контуру Г
производится в отрицательном направлении,
будем писать
понимать интеграл вдоль контура Г
в положительном направлении (т.е. когда
область ограниченная кривой Г ,
остается слева при движении по Г).
Когда интегрирование по контуру Г
производится в отрицательном направлении,
будем писать
![]()
