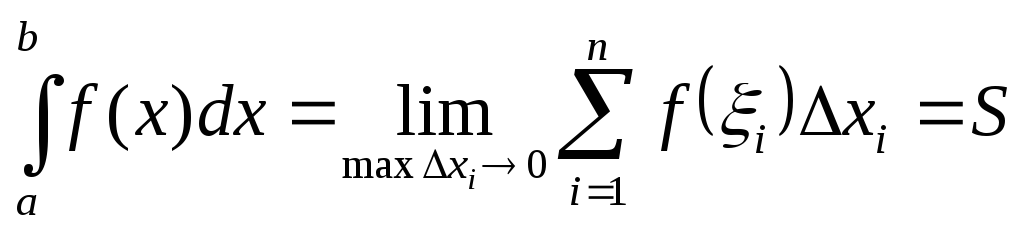7.2. Определенный интеграл

Интеграл можно определить как предел интегральных сумм.

Таблица 7

Определенный интеграл функции f(x) на отрезке [a, b]
Геометрический смысл определенного интеграла

С помощью интегральных сумм можно приближенно вычислять самые разные величины (рис. 10).

Интегралом от а до b функции f называется приращение первообразной F этой функции: F(b}—F(a) - (формула Ньютона — Лейбница.

Примеры: Вычислить

Упражнение. Найти числа, получающиеся при использовании в интеграле следующих функций:

Ответ: 1) 1/2; 2) 3/8.

Пример. Вычислить площадь, ограниченную кривой y=sinx и осью абсцисс, если х [0, ].

Для ответа на поставленный вопрос следует вычислить интеграл

Упражнение. Найти площадь плоской фигуры, ограниченной параболой у = х² +1,осью Ох и прямыми х:=1 и х=4.

Ответ. 24.

Пример. Интегрирование по частям в определенном интеграле:

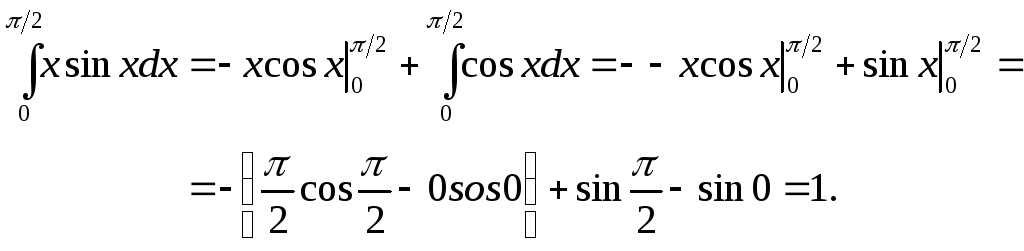
Здесь U=x, dU=dx, dV=sinxdx, V=-cosx.

Упражнения.

Контрольные вопросы и упражнения

1. Запишите свойства первообразной.

2. Выпишите основные табличные интегралы по схеме

3. Приведите примеры «неберущихся» интегралов,

4. Найдите:a) ; б) ; в) .

5. Дайте определение определенного интеграла. Каков его геометрический смысл?

6. Сформулируйте и запишите основные свойства определенного интеграла.

7. Вычислите .

8. Найдите площадь фигуры, ограниченной линиями . Сделайте чертеж.

Математик, оперируя множеством символов, явно имея дело с чисто формальными истинами, тем не менее может достичь бесконечно важных результатов для описания физического мира.

К. Пирсон

8. Дифференциальные уравнения

Многочисленные задачи естествознания, техники и других областей знания сводятся к тому, что по заданным свойствам некоторого процесса или явления необходимо найти математическую модель самого процесса в виде формулы, связывающей переменные величины, т.е. в виде функциональной зависимости. Уравнения, в которых содержатся производные или дифференциалы искомых функций, называются дифференциальными. Они являются мощным средством познания окружающего нас мира. Дифференциальное уравнение — это как бы мгновенный снимок процесса в данный момент времени; интегрируя дифференциальное уравнение, мы по мгновенным снимкам восстанавливаем течение процесса в целом.

Обыкновенным дифференциальным уравнением (ДУ) называется уравнение, в котором неизвестной является функция одного независимого переменного, причем в уравнение входят производные различных порядков. В самом общем виде ДУ записывается так:

F(x,y,y',y",...,y⁽ⁿ⁾) = 0.

Порядок старшей производной, входящей в состав уравнения, называется порядком уравнения. Решением ДУ называется функция у = (x), обращающая это уравнение в тождество.

Пример. Функция у = Сх + х² является решением уравнения , так как она обращает это уравнение в тождество.

Дифференциальные уравнения первого порядка F(x, у, у') = 0
Формы записи
Основные типы
Уравнения с разделяющимися переменными	Однородные уравнения	Линейные уравнения

График решения называется интегральной кривой, а процесс нахождения решений — интегрированием ДУ. Следует отметить, что методы решения ДУ разнообразны и зависят от вида (порядка первого, второго, ...), типа (с разделяющимися переменными, однородные, линейные, ...) и т.д.

Использование операции интегрирования связано с появлением произвольной постоянной. Если действие повторяется n раз, то, очевидно, и в решении будет содержаться n произвольных постоянных.

Общим решением ДУ называется функция вида

Пример. Уравнение имеет общее решение (проверьте!).

Если постоянным С_i придать конкретные числовые значения, то полученная функция носит название частное решение.

Задача нахождения частного решения ДУ, удовлетворяющего начальному условию у = y₀ при х =x₀ называется задачей Коши (по имени французского математика).

Пример. Задача о законе естественного роста.

Закон естественного роста это закон, при котором скорость роста вещества прямо пропорциональна его количеству. Найдем формулу для определения изменения количества вещества у в зависимости от времени х, считая, что в начальный момент при х=0 количество вещества было у₀. Используя физический смысл производной, этот закон можно записать так:

где k — коэффициент пропорциональности. Уравнение описывает многие процессы «размножения». Решение уравнения, удовлетворяющее начальному условию у= y₀ при x=0, имеет вид . Представляет интерес то, что по этой формуле, выражающей закон «естественного роста», происходит и «размножение» числа нейтронов в ядерных реакциях, и размножение числа бактерий, и рост населения и т.п.

Упражнения. Найдите частные решения уравнений: