Абсолютная величина действительного числа. Окрестность точки

Абсолютной величиной (модулем) действительного числа называется .

По определению, очевидно, что .

Свойства абсолютных величин:

1. ; 2.

3. ; 4. .

Абсолютная величина разности двух чисел означает расстояние между точками и числовой прямой как для случая , так и для . Поэтому, например, решениями неравенства будут точки интервала , удовлетворяющие неравенству .

Всякий интервал, содержащий точку , называется окрестностью точки .

Интервал , т.е. множество точек таких, что , называется -окрестностью точки .

Понятие функции одной переменной

Постоянной величиной называется величина, сохраняющая одно и то же значение.

Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу .

Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.

Переменной называется величина, которая может принимать различные числовые значения.

Например, при равномерном движении , путь и время - переменные величины, а скорость - параметр.

Перейдем к понятию функции.

Определение. Если каждому элементу ставится в соответствие вполне определенное значение множества , то говорят, что на множестве задана функция .

При этом называется независимой переменной, или аргументом, а - зависимой переменой, буква обозначает закон соответствия.

Множество называется областью определения, или существования функции, а множество - областью значений функции.

Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл.

Например, область определения функции есть полуинтервал , так как .

Способы задания функции

Существует несколько способов задания функции.

а) Аналитический способ, если функция задана формулой вида . этот способ наиболее часто встречается на практике;

б) Табличный способ, если функция задана таблицей, содержащей значения аргумента и соответствующие значения функции , например, таблица логарифмов;

в) Графический способ, если функция изображена в виде графика – множества точек плоскости, абсциссы которых есть значения аргумента , а ординаты – соответствующие им значения функции ;

г) Словесный способ, если функция описана правилом ее составления, например, функция Дирихле¹: , если - рационально; , если - иррационально.

Основные свойства функций

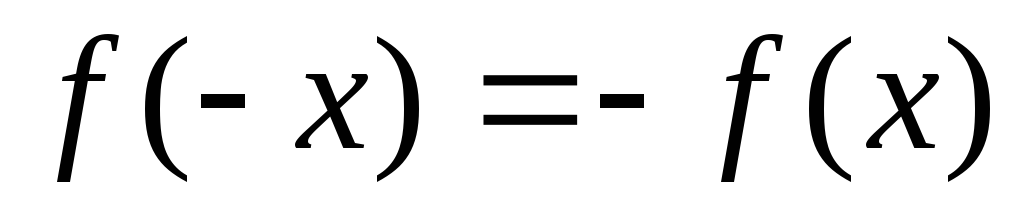1. Четность и нечетность. Функция называется четной, если для любых значений из области определения , и нечетной, если . В противном случае функция называется функцией общего вида.

Например, функция - четная, так как , а функция - нечетная, так как . В то же время, например, функция является общего вида, так как и , .

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

2. Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть и . Тогда функция возрастает на промежутке , если , и убывает, если .

3. Ограниченность. Функция 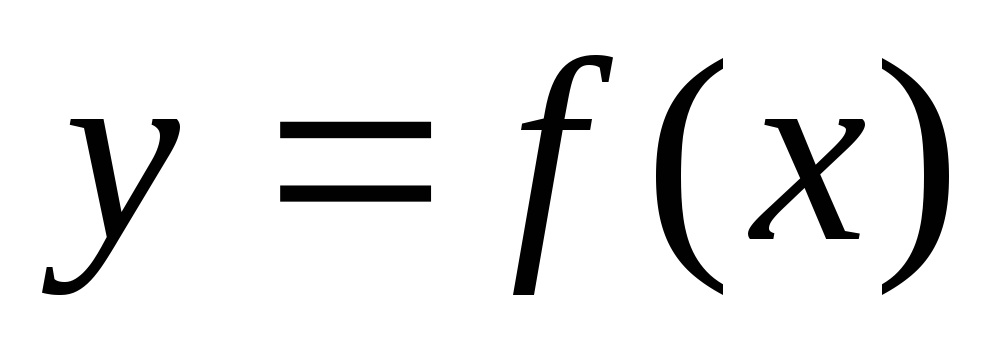называется ограниченной на промежутке , если существует такое положительное числ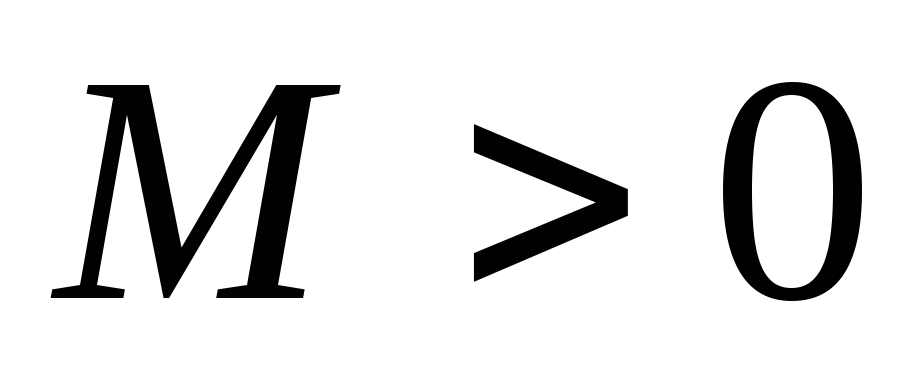о , что 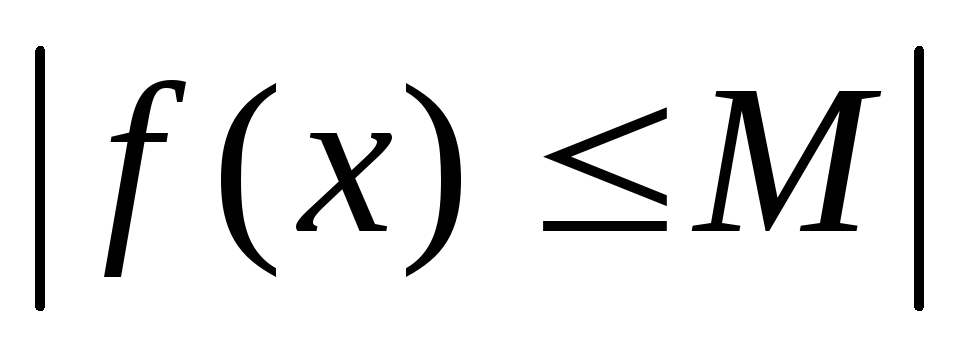для любого. В противном случае функция называется неограниченной.

Например, функция ограничена на всей числовой оси, так как для любого .

4. Периодичность. Функция называется периодической с периодом , если для любых из области определения функций . Например, функция имеет период (наименьший положительный период) , так как для любых значений .

График периодической функции может быть получен сдвигом кривой вправо (влево) на отрезки