17. Средняя арифметическая

Средняя арифметическая простая (невзвешенная) равна сумме индивидуальных значений признака, деленной на число этих значений:

где xi – индивидуальные значения признака (варианты); n – число единиц совокупности. Простая средняя арифметическая применяется в тех случаях, когда имеются индивидуальные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется с помощью весов. Средняя арифметическая взвешенная имеет вид:

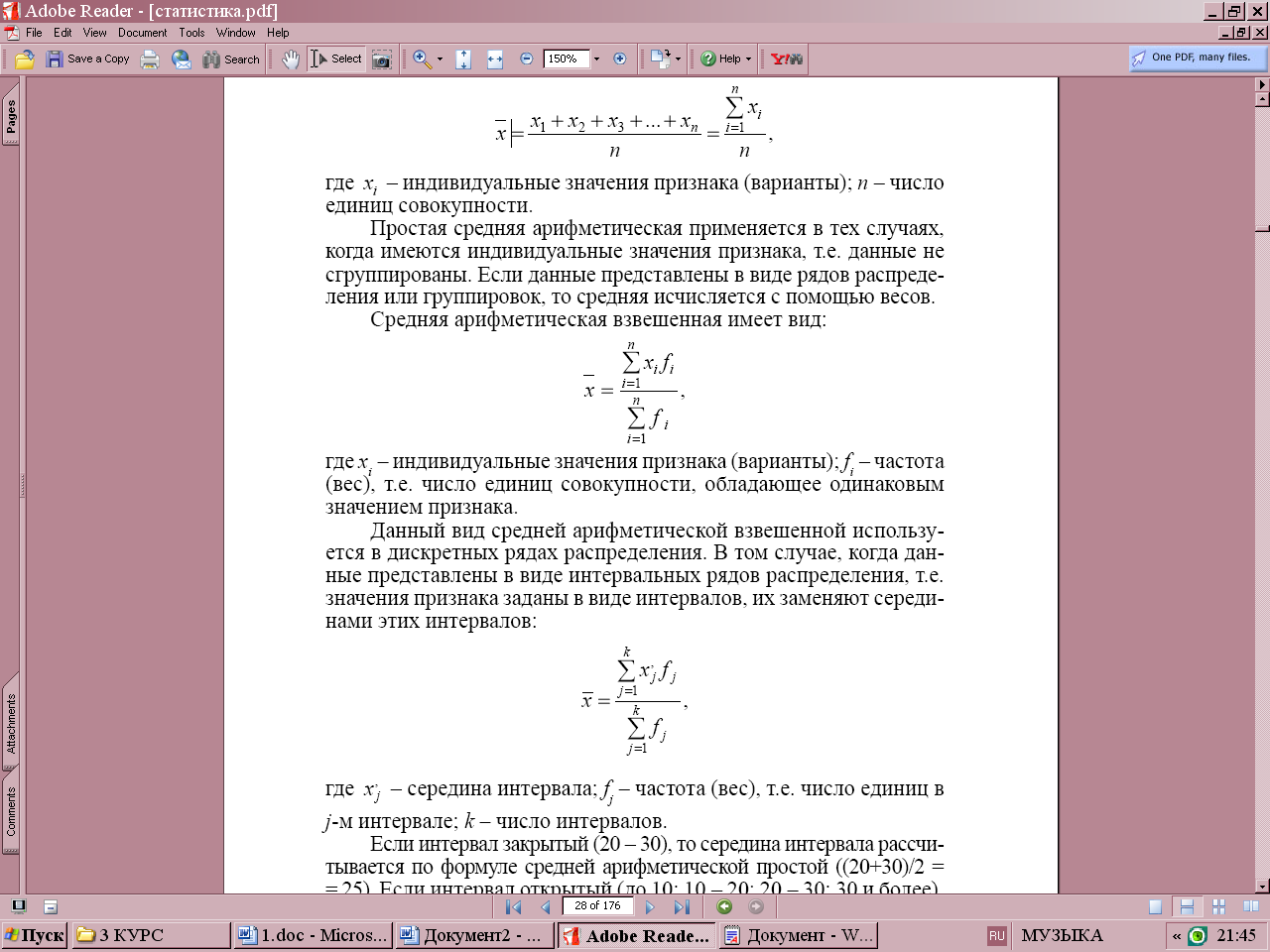где xi – индивидуальные значения признака (варианты); fi – частота

(вес), т.е. число единиц совокупности, обладающее одинаковым значением признака.

Данный вид средней арифметической взвешенной используется в дискретных рядах распределения. В том случае, когда данные представлены в виде интервальных рядов распределения, т.е. значения признака заданы в виде интервалов, их заменяют серединами этих интервалов:

где ,x j – середина интервала; fj – частота (вес), т.е. число единиц в j-м интервале; k – число интервалов. Если интервал закрытый (20 – 30), то середина интервала рассчитывается по формуле средней арифметической простой ((20+30)/2 == 25). Если интервал открытый (до 10; 10 – 20; 20 – 30; 30 и более), то величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы – величине предыдущей. Дальнейший расчет аналогичен изложенному выше ((0+10)/2 = 5); (30+40)/2 = 35).Особое внимание следует уделить расчету средних величин относительных признаков. При вычислении таких средних величин необходимо, чтобы сохранялась неизменной сумма величины объемного признака, который является числителем при построении усредняемого относительного показателя. Чтобы выполнить это условие, в качестве весов при расчете средней величины относительного показателя необходимо принять значения того признака, который является знаменателем при определении относительного показателя.

18. Виды средних величин

Обусловленность выбора средней характером исходной информации.

Гармоническая:

Хгарм=n / ( 1/xi) простая

Если не известны частоты, но известны объемные значения признака используют сложную:

Хгарм=i/ i /xi) i=xifi

Средняя квадратическая

Хкв=(корень квадратный) хi/n (простая) Х=(корень квадратный) xi2fi / fi (сложная)

Средняя кубическая

Х=(корень кубический) xi3 / n (простая) X=(корень кубический) xi3fi / fi (сложная)

Средняя геометрическая

Х=(корень n-ой степени) х1*х2*х3*….*хn (простая) Х=(корень n-ой степени) x1f1*x2f2*…*xnfn (сложная)

Все перечисленные виды средних принадлежат к общему типу – степенной средней Х=(корень k-ой степени) xik / n

В широком понимании термина средней величины ею является всякий обобщающий показатель, характеризующий обобщенные значения признака их динамики и структуры в совокупности массовых явлений.

Понятие средней сближается с философской категорией закон. Рассмотрим процесс осреднения и отметим, что средняя рассчитывается по однородной совокупности. Однородное индивидуальное значение признака – это проявление общих свойств, обусловленные основными условиями и закономерностями массовых процессов. Однако кроме общих условий, кроме закономерности, на каждую единицы совокупности влияют индивидуальные, особенные условия, случайные события, несвязанные причиной, но с общей закономерностью. Таким образом, индивидуальные значения признака можно обозначитьX=c+i c-закономероности i – случайность

Вычислим среднее значение X=xi / n=(c+i) / n = (nc+in) / n = c+i .При осреднении элементы случайности, согласно закону больших чисел взаимопогашаются тем в большей мере, чем больше объем совокупности. Тем с большей вероятностью среднее значение признака измеряет действие общих для совокупности закономерностей.

19. Структурные средние (Мода и медиана), Для характеристики среднего значения признака в вариационном ряду используются показатели центра распределения, к которым, кроме средней арифметической величины, относятся мода и медиана. Также существуют другие показатели, характеризующие структуру вариационного ряда.Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности. Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Для интервальных вариационных рядов мода определяется по формуле:

где хМо– нижняя граница значения интервала, содержащего моду; iМо– величина модального интервала; fМо– частота модального интервала, т.е. интервала, имеющего наибольшую частоту; fМо-1 –частота интервала, предшествующего модальному, fМо+1 – частота интервала, следующего за модальным. Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, делящее ее на две равные части. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Медиана интервального ряда распределения определяется по формуле

где xMе – нижняя граница значения интервала, содержащего медиану; iМе– величина медианного интервала; – сумма частот; SМе-1 – сумма накопленных частот, предшествующих медианному интервалу; fМе – частота медианного интервала. Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равные части, десять или сто частей. Эти величины называются квартили, децили и перцентили. Остановимся на расчете показателей децилей, нашедших широкое применение в анализе дифференциации различных социально-экономических явлений.