3 Построение доверительных интервалов
При построении доверительных интервалов для математического ожидания, дисперсии и среднеквадратического отклонения используются выводы результатов характеристик переменных, полученных с применением функции «Descriptive statistics» - пункт 1 (рис.8)
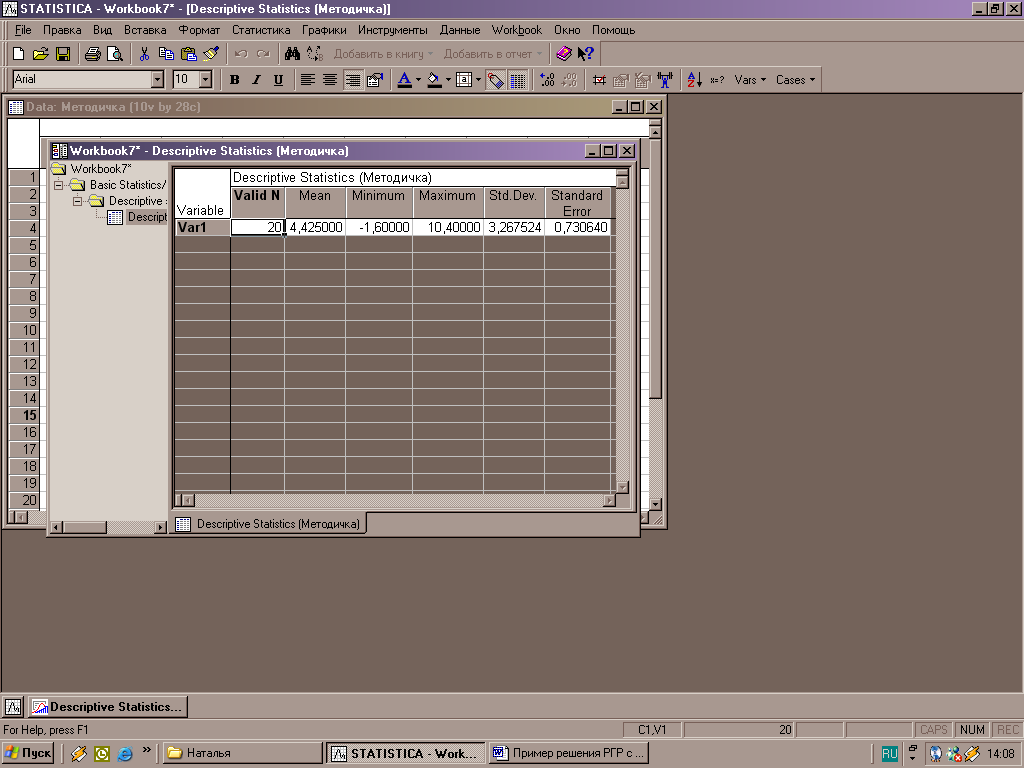
Рисунок 8 – Основные характеристики переменной х
4 Расчет парного коэффициента корреляции
Для нахождения парного коэффициента корреляции между двумя переменными х и у обращаются к меню «Основная статистика», где выбирают функцию «Correlation matrices» (рис.2). В меню ввода данных выбранного анализа (рис.9) вводят переменные, между которыми требуется вычислить коэффициент корреляции. Итоговое окно содержит значение коэффициента между рассматриваемыми переменными (рис.9).
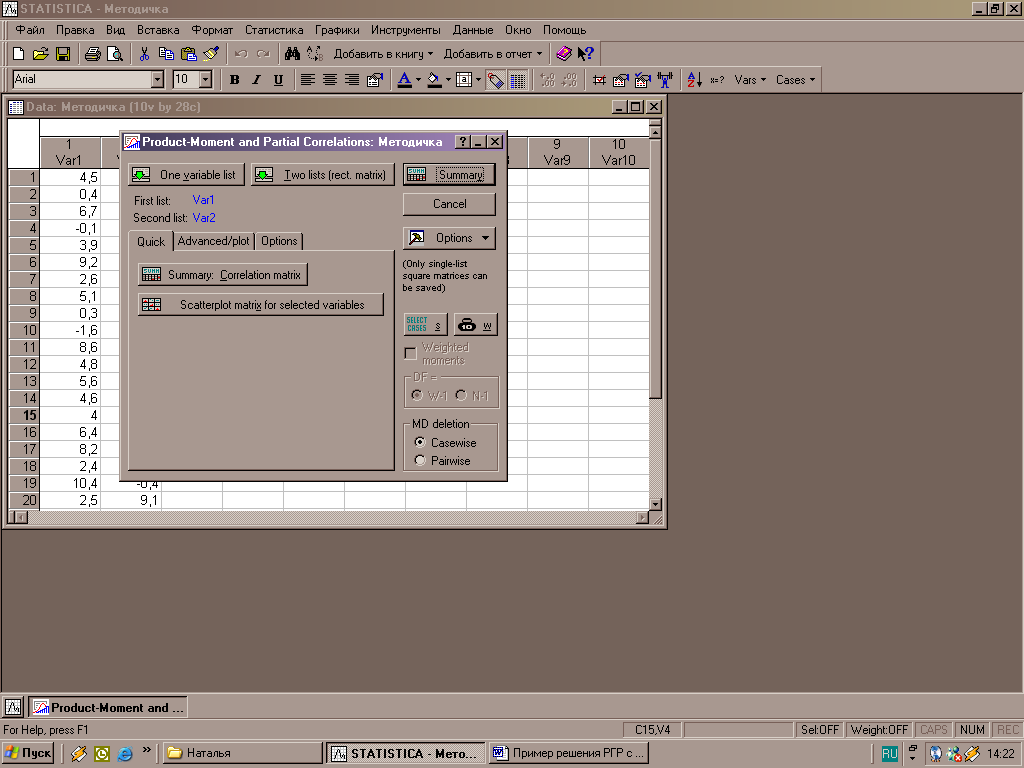
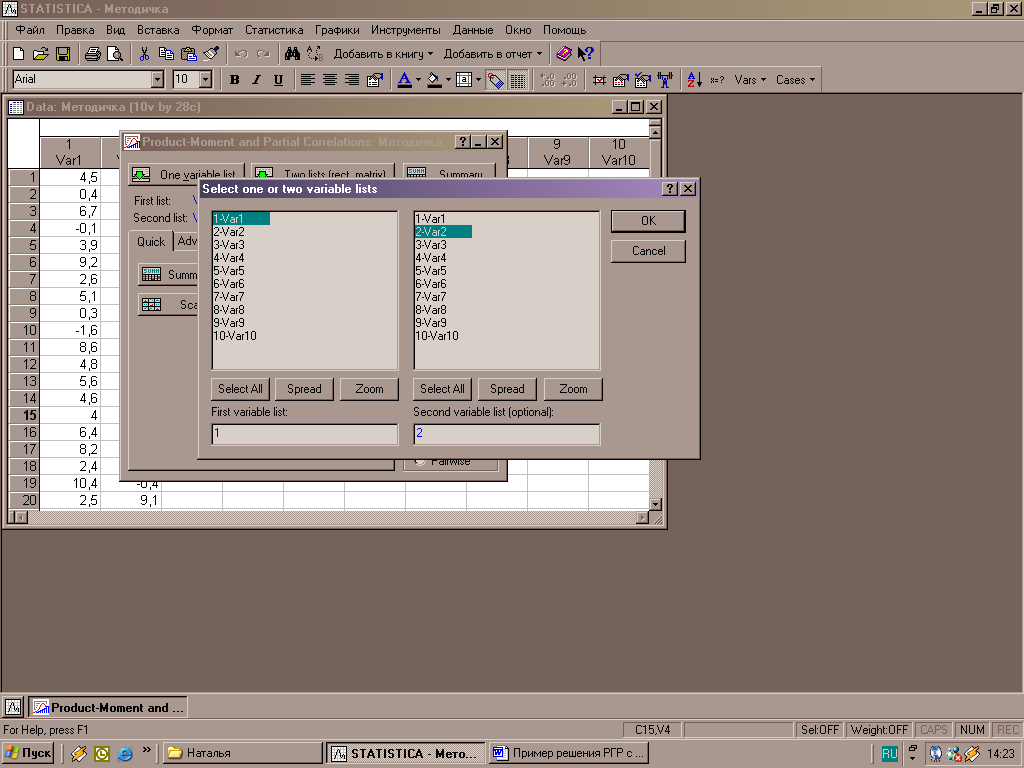
Рисунок 9 - Окна ввода данных для вычисления коэффициента корреляции
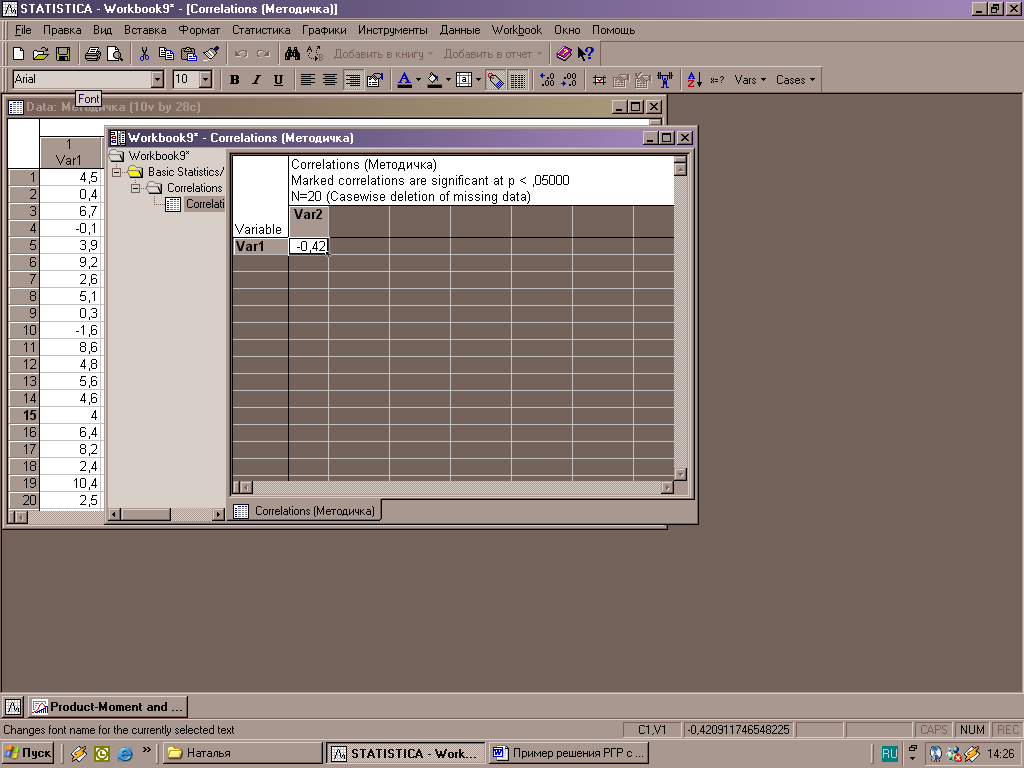
Рисунок 9 – Вывод значения коэффициента корреляции
5 Проверка значимости коэффициента корреляции
С вероятностью р<0,05 значимые парные коэффициенты в пакете Statistica 6.0. выделяются красным, однако, для рассматриваемого примера коэффициент незначим.
6 Построение уравнения регрессии
Для построения уравнения регрессии в меню «Статистика» выбирают функцию– «Множественная регрессия», после чего активизируется окно выбранного анализа и предлагается сделать выбор зависимой и независимой переменных (рис. 10).
Рисунок 10 – Окно «Множественная регрессия»
После выбора переменных и вывода необходимых характеристик появляется итоговое окно (рис.11), содержащее основные характеристики уравнения регрессии: множественный коэффициент корреляции, стандартные ошибки.
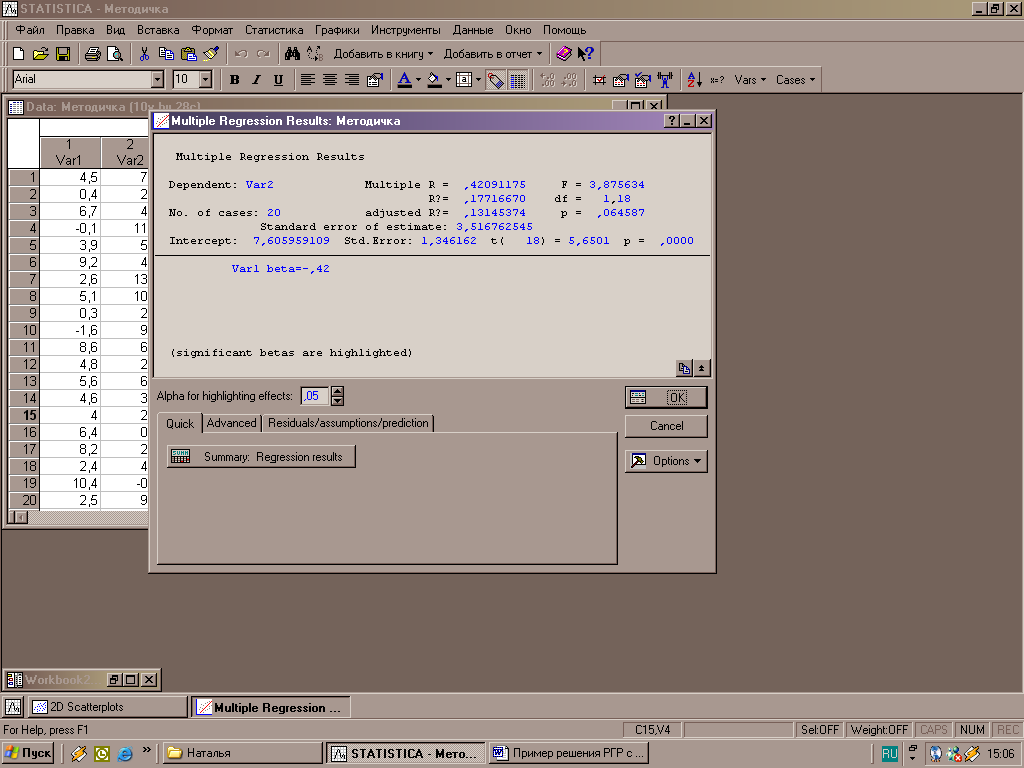
Рисунок 11 – Итоговое окно «Множественная регрессия»
Для вывода значения коэффициентов регрессии активизируют кнопку «Суммарный регрессионный результат», находящаяся в нижнем левом углу, после чего появляется окно вывода данных (рис.12).
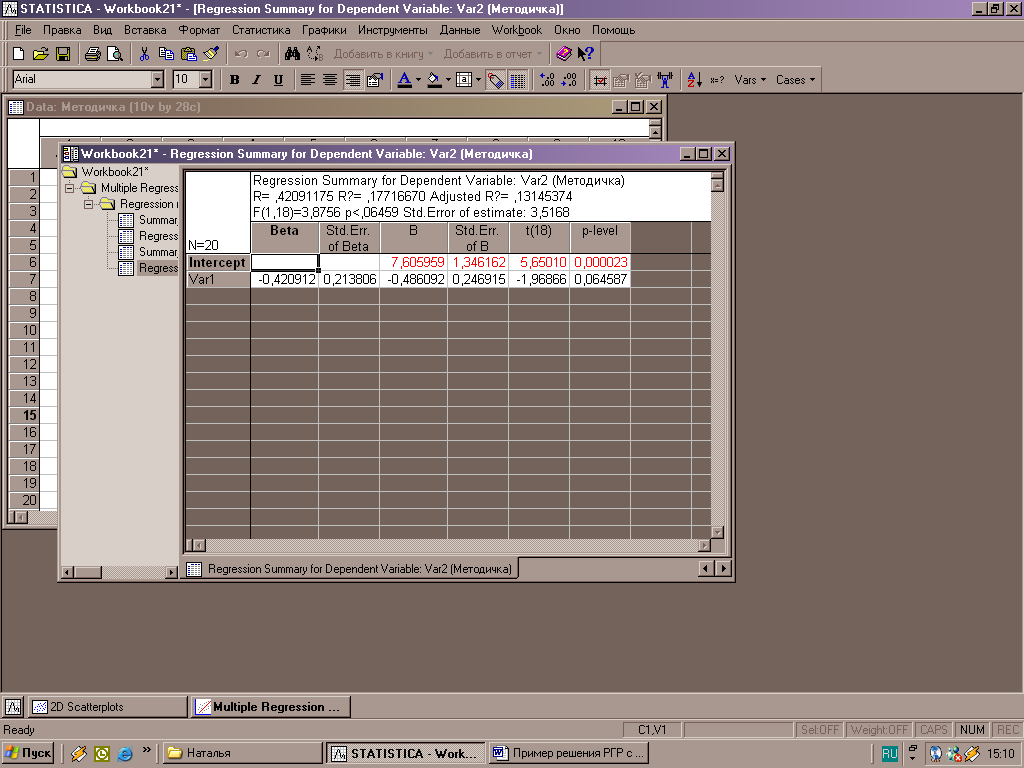
Рисунок 12 – Вывод значений коэффициентов регрессии
Значимые коэффициенты регрессии выделяются красным - для рассматриваемого примера значимым является коэффициент β0.
7 Литература
1. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2002.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001.
3. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1990.
4. Калинина В.Н., Панкин В.Н. математическая статистика. – М.: Высшая школа, 2001.
5. Мхитарян В.С., Трошин Л.И. Задачник по дисперсионному, корреляционному и регрессивному анализу. – М.: МЭСИ, 1996.
6. Дуброва Т.А., Павлов Д.Э., Ткачев О.В. Корреляционно-регрессионный анализ в системе "Statistica". Методические указания. - М.: МЭСИ, 1996- 70с.
7. Реннер А.Г., Аралбаева Г.Г. Корреляционно-регрессионный анализ. Методические указания к лабораторному практикуму. – ОГУ, Оренбург, 2002.
8 Приложение
