6 Проверка гипотезы о равенстве генеральных средних двух нормально распределенных случайных величин X и y
Выдвигаем гипотезу:
Т.к. генеральные дисперсии неизвестны, то с учетом результатов расчета п.5, выбираем статистику
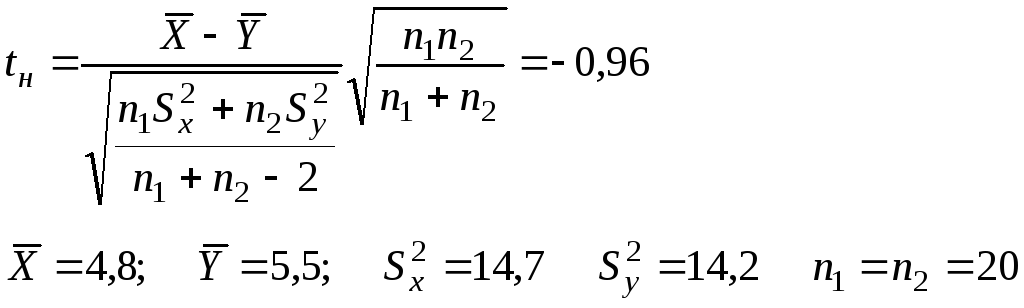
Находим tкр по табл. П4 =0,05 и число степеней свободы =n1+n2-2=20+20-2=38
т.к.
нулевая гипотеза принимается с уровнем значимости α=0,05, критическая область двусторонняя.
7 Построение доверительных интервалов для генеральных средних нормально распределенных совокупностей
7.1 Построение доверительного интервала для генеральной средней совокупности х
Т.к. генеральная дисперсия неизвестна, используем статистику
где
–
выборочное среднее значение;
Sх – выборочное среднеквадратическое отклонение;
n – объем выборки;
tα –статистика, имеющая распределение Стъюдента и для числа степеней свободы n-1=20-1=19 и α=0,05 t0,05=0,1
Подставляя ранее найденные параметры получаем:
И окончательно доверительный интервал для математического ожидания примет вид:
7.2 Построение доверительного интервала для генеральной средней нормальной совокупности случайной величины У
Аналогичным
образом построим доверительный интервал
для совокупности У, используя статистику
п.7.1 и ранее найденные оценки SУ=3,7
и
Для У доверительный интервал примет вид:
8 Построение доверительных интервалов для генеральных дисперсий
8.1 Построение доверительного интервала для генеральной дисперсии нормальной совокупности случайной величины Х
Т.к. математическое ожидание генеральной совокупности Х неизвестно и объем выборки меньше 30, используем статистику
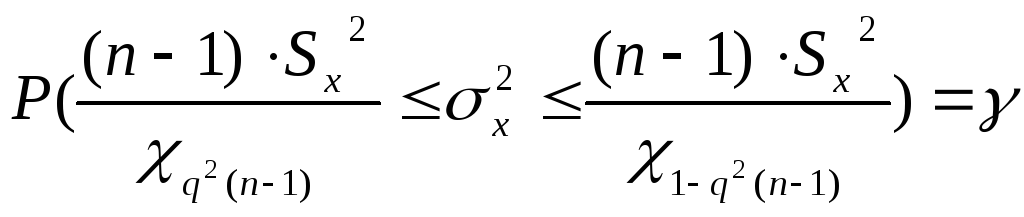
где χq2(n-1) и χ 1- q2(n-1) распределены по закону χ2 и находятся по таблице χ2 - распределения с числом степеней свободы υ = (n-1)=20-1=19, q= 1-α/2 и 1-q.
χ2 0,9752(20-1)=30,144 и χ2 0,025 (20-1)=10,117.
8.2. Построение доверительного интервала для генеральной дисперсии нормальной совокупности случайной величины У.
Аналогично п.8.1 используем статистику
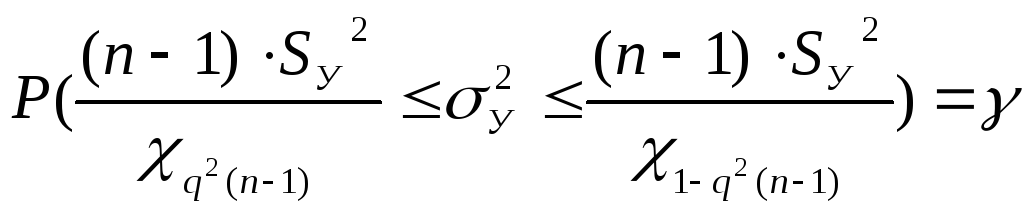
Согласно п. 2.2 S2У = 14,2 и доверительный интервал для генеральной дисперсии совокупности У:
9 Построение доверительных интервалов для среднеквадратических отклонений
9.1 Построение доверительного интервала для среднеквадратического отклонения нормальной совокупности случайной величины Х
Доверительный интервал для среднеквадратического отклонения строится на основе статистики, использующейся при построении интервала для дисперсии:
9.2 Построение доверительного интервала для среднеквадратического отклонения нормальной совокупности случайной величины У
Аналогично доверительный интервал для среднеквадратического отклонения совокупности У:
10 Расчет парного коэффициента корреляции
Выборочный парный коэффициент корреляции находится по формуле:
Для рассматриваемых данных
.
11 Проверка значимости парного коэффициента корреляции
При проверке значимости парного коэффициента корреляции выдвигают гипотезы:
По табл. П5 Фишера-Иейтса для =0,05 и =n-2=20-2=18 найдем табл=0,444
т.к.
,
то нулевая гипотеза с вероятность. 0,95
отвергается и парный коэффициент
корреляции между исследуемыми случайными
величинами является значимым.
12 Построение доверительного интервала для парного коэффициента корреляции
Для значимого парного коэффициента целесообразно построить доверительный интервал, используя Z-преобразование Фишера
На первом этапе вычисляем величину Z:
По табл. П6 Z-преобразований Фишера для найденного значения Z найдем значение Zr=0,6184.
При доверительной вероятности 0,95 по табл. П1-нормальный закон распределения- найдем t=1,96
Доверительный интервал для математического ожидания величины Zr найдем по формуле:
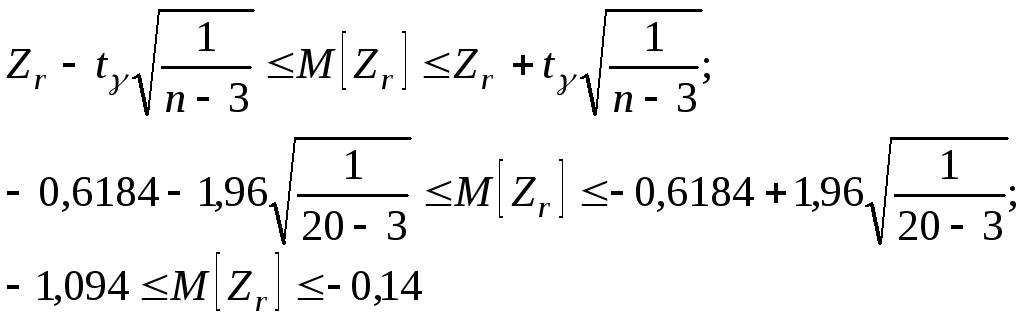
Используя табл. П6 Ζ- преобразования Фишера найдем доверительный интервал для коэффициента корреляции
13 Построение уравнения регрессии
Необходимо найти уравнение в виде:
где оценкой 1 является
Оценкой 0 является
И тогда уравнение для рассматриваемых данных примет вид:
14 Проверка значимости уравнения регрессии
При проверке значимости уравнения регрессии, проверяют значимость соответствующего коэффициента регрессии. Если коэффициент значим, то и значимо уравнение регрессии.
Используем статистику:
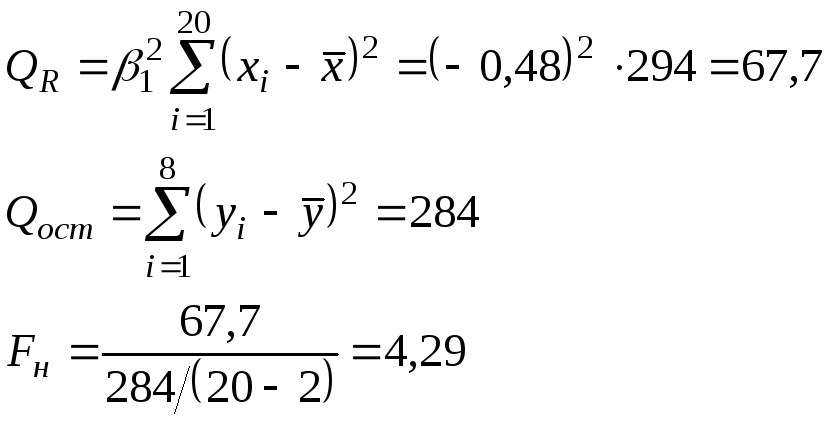
По табл. П4 Фишера-Снедекора при =0,05 и 1=2=n-1=20-1=19
Fкр=2,16
Т.к. Fн>Fкр (4,29>2,16) гипотеза H0 отвергается, т.е. уравнение регрессии является значимым.
15 Построение доверительных интервалов для найденных оценок коэффициентов регрессии 0 и 1
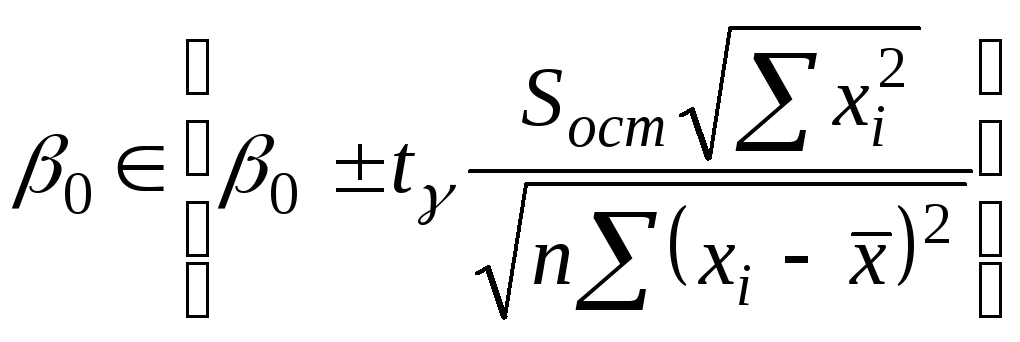
по таблице П2-распределение Стьюдента при =0,05 и =18 t=1,1,
где
Для 1:
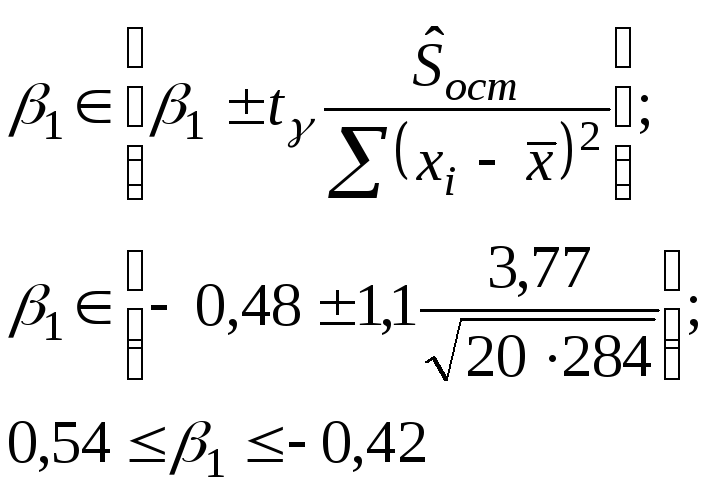
16
Построение доверительного интервала
для математического ожидания
при заданном x0=15
По табл. П2 при =0,05 и =n-2=18 t=1,1.
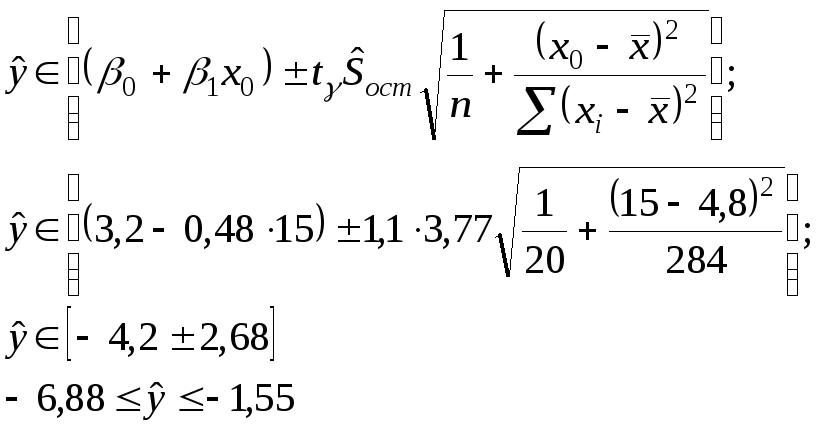
17
Определение доверительного интервала
предсказания
При =0,9 интервал предсказания высчитывают по следующей формуле, подставляя раннее вычисленных характеристики совокупности:
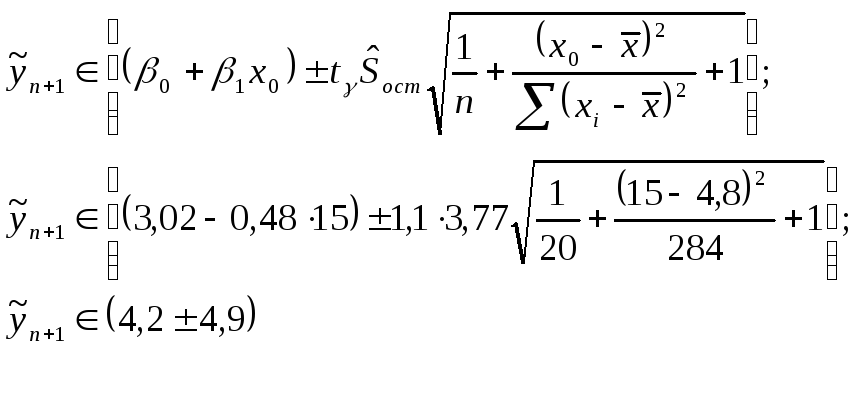
И
интервал предсказания в точке
:
