6 Пример расчета и оформления ргр

Исходные данные:

X	4,5	0,4	12,7	-0,1	3,9	9,2	2,1	5,1	0,3	-1,6	8,6	4,8	8,5	4,6	4,0	6,4	8,2	2,4	10,4	2,5
Y	7,9	2,6	4,5	11,3	5,4	4,5	13,5	10,1	2,3	9,6	6,6	2,6	6,7	3,3	2,2	0,7	2,5	4,1	-0,4	9,1

m_0x=5,5; m_0y=6; _0x²=15; _0y²=12; x₀=15;

1 Построение гистограммы и статистической функции распределения

1.1 Случайная последовательность X

Ii	1,26 -1,6	1,26 4,12	4,12 6,98	6,98 9,84	9,84 12,7
mi	4	5	5	4	2
	0,2	0,25	0,25	0,2	0,1

1 0,45 .2 Случайная последовательность y

Ii	-0,4 2,38	2,38 5,16	7,94 5,16	7,94 10,72	10,72 13,5
mi	4	7	4	3	2
	0,2	0,35	0,2	0,15	0,1

2 Проверка гипотез о законах распределения генеральных совокупностей

2.1 Проверка гипотезы о нормальности распределения генеральной совокупности X

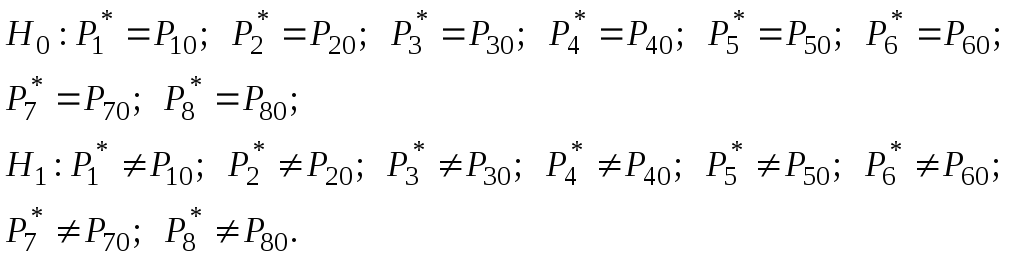
Проверку гипотезы проводим на уровне значимости =0,05.

Для проверки гипотезы используем критерий согласия ² Пирсона.

Ii	-1,6 0,18	0,18 1,98	1,98 3,77	3,77 5,56	5,56 7,35	7,35 9,12	9,12 10,92	10,92 12,7
mi	2	2	3	6	1	3	2	1

Определяем вероятность попадания случайной величины в каждый интервал.

где  и  - границы интервалов.

В качестве математического ожидания m_x используем точечную оценку m_x:

Точечная оценка для дисперсии случайной величины X:

Оценка среднего квадратического отклонения

Используя таблицу П.1- нормальный закон распределения, получаем

0,08

0,11

0,13

0,14

0,15

0,11

0,08

0,06

Учитывая, что n=20, найдем значение ²:

сходится (при ) к - распределению,

где l – общее число интервалов группирования;

k- число неизвестных параметров, оцененных по выборке.

Далее по заданному уровню значимости критерия α и числом степеней свободы l-k-1 из таблиц - распределения (таблица П.3) находят 100(1-α/2)% и 100α/2%-ые точки и и если

<<,

то нулевая гипотеза принимается - выборочные данные распределены по нормальному закону.

При α = 0,05, количестве интервалов группирования l =8, числе оцененных параметров по выборке k=2 значения критических точек будут:

и .

Так как наблюдаемое значение попадает в интервал, то делаем вывод о том, что нулевая гипотеза принимается и генеральная совокупность, представленная выборкой Х подчинена нормальному закону распределения.