Рекомендации по использованию ппп при решении ргр
В качестве вспомогательных электронно-вычислительных средств для решения задач РГР рекомендуется использование таких программных модулей как: Stadia, Excel, Statistica.
Пример решения РГР приведен с использованием статистического пакета Statistica 6.0.
Данные вводятся в среду пакета, где переменной 1 – соответствуют значения х, переменной 2 – значения у ( рис.1).
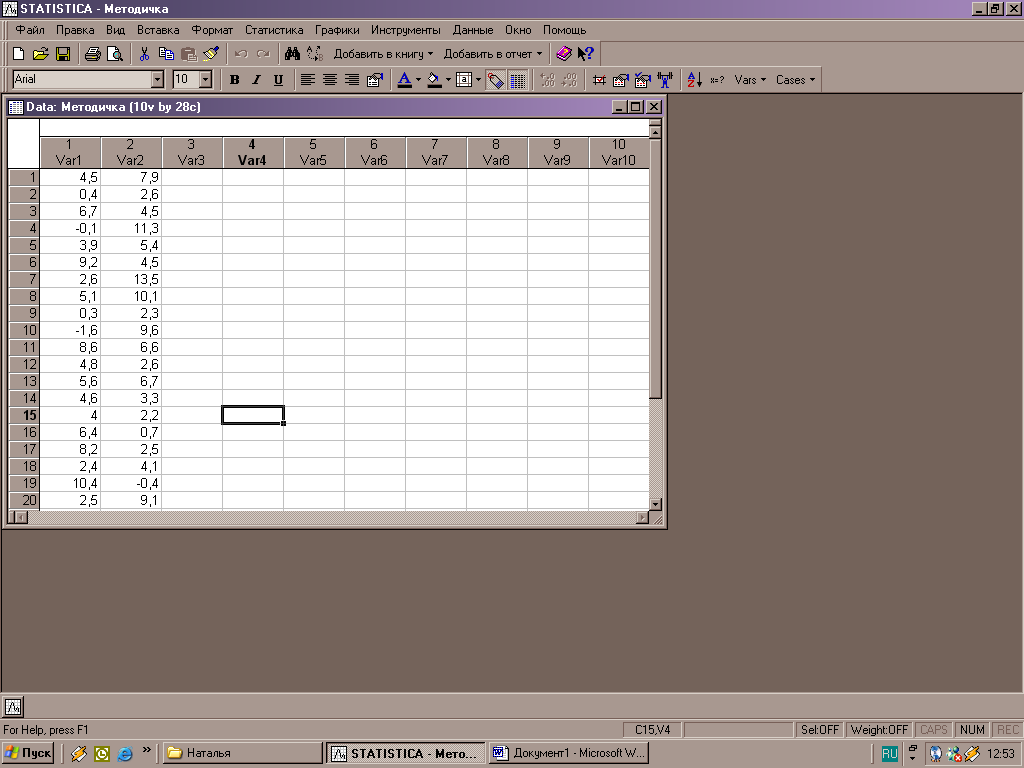
Рисунок 1 – Ввод исходных данных
-
Построение гистограммы и статистических функций распределения
На панели инструментов, в статистике, выбирают функцию «Основная статистика», после чего активизируется соответствующее окно (рис.2).
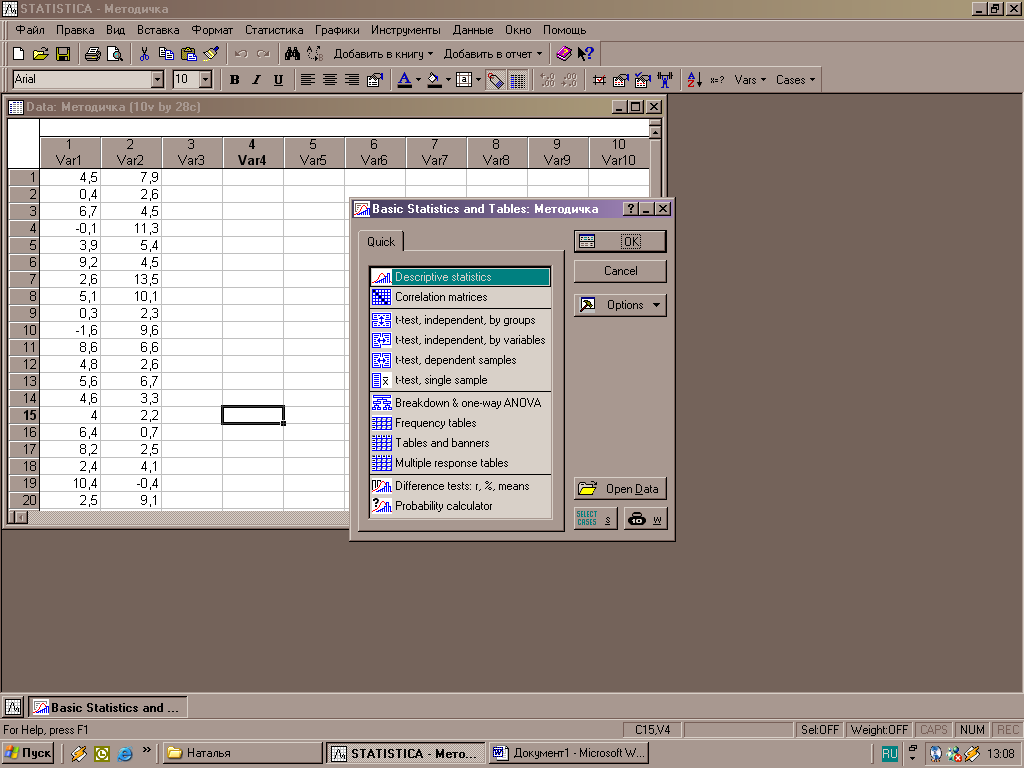
Рисунок 2 – Выбор основной статистики.
Где для дальнейшего анализа выбираем функцию – «Descriptive statistics» и далее появляется окно запрашиваемой функции, предлагающего выбор переменных и ввод основных характеристик (рис.3).
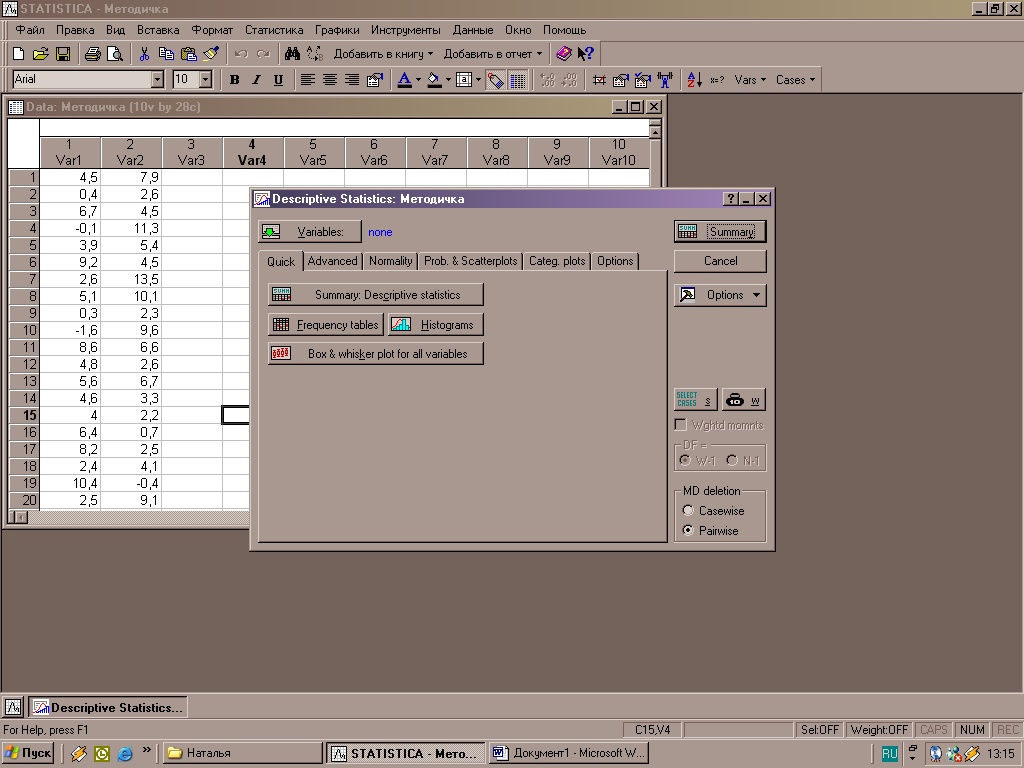
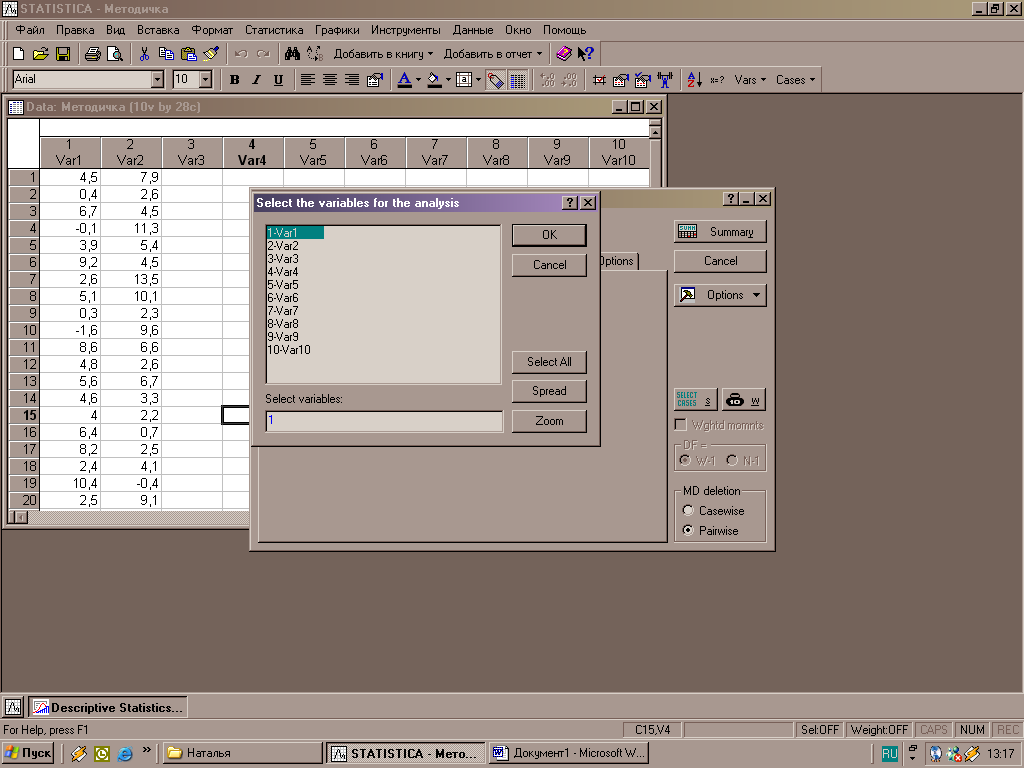
Рисунок 3 – Окна ввода данных
С помощью кнопки Summary: Discriptive statistics на экран выводятся значения основных характеристик переменной – рисунок 4 (дополнительные характеристики можно выбрать посредством опции Advanced):
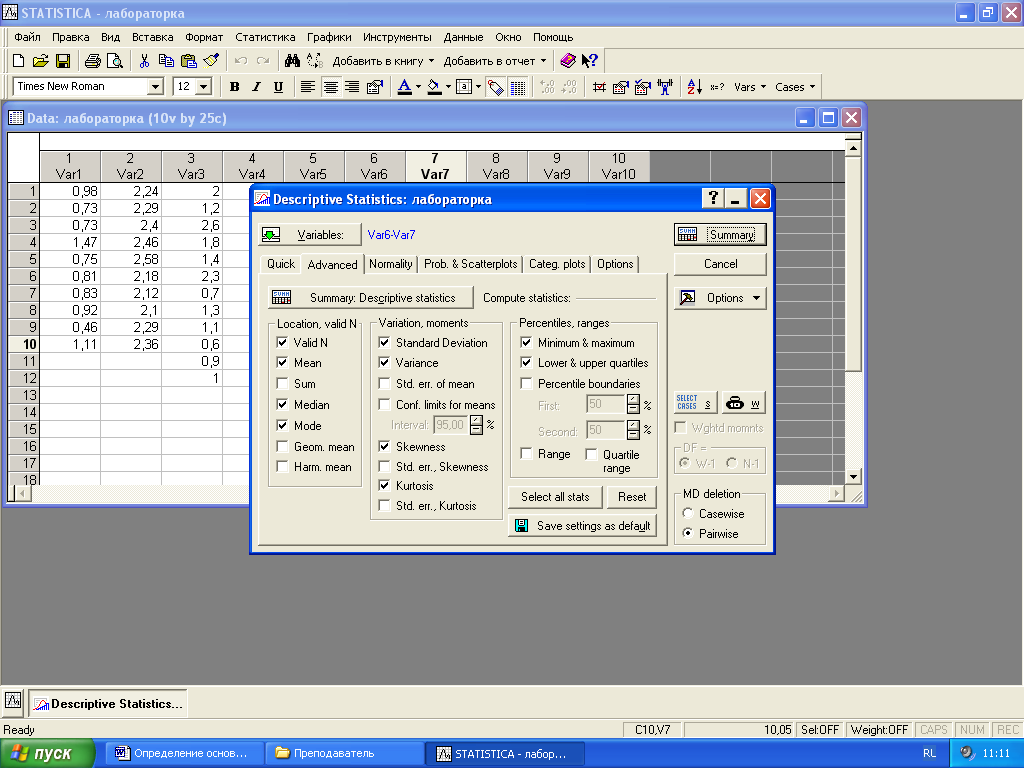
Рисунок 4 – выбор дополнительных числовых характеристик,
где:
Maximum & Minimum - минимальное и максимальное значения выборки;
Mean - среднее значение
Mode - мода
Median - медиана
Standard Deviation - среднеквадратическое отклонение
Variance - дисперсия
Skewness - асимметрия
Kurtosis - эксцесс.
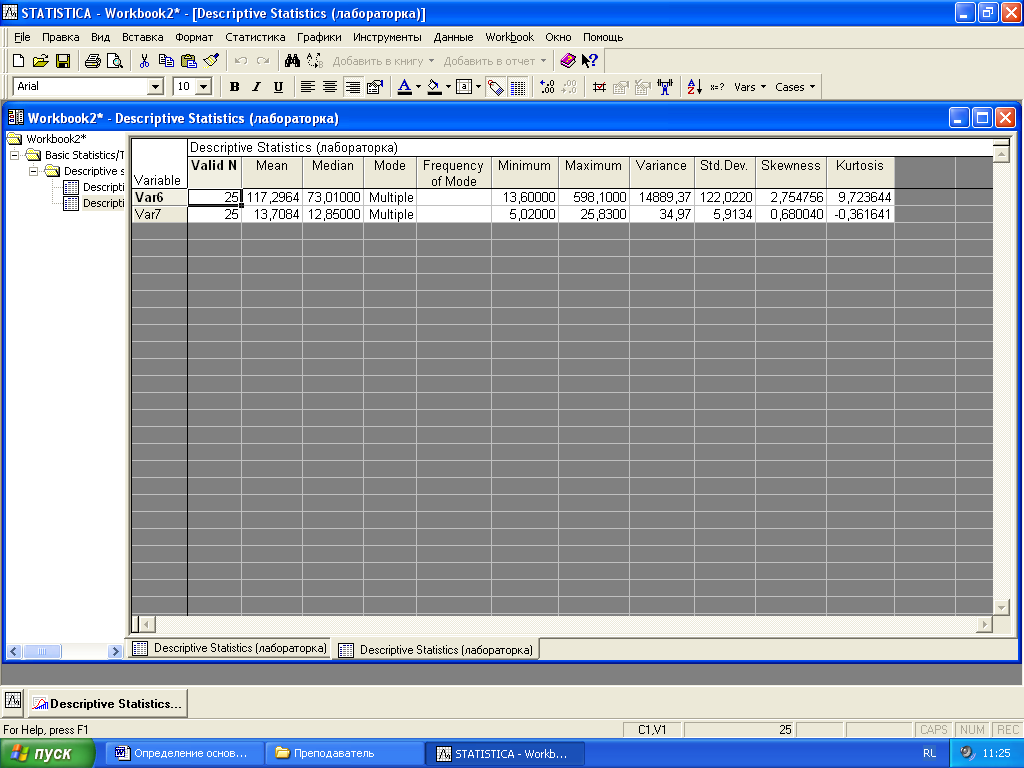
Рисунок 5 – Вывод основных числовых характеристик
Для вывода гистограммы служит кнопка «Histograms». После выбора необходимого действия – построение гистограммы - появляется окно вывода результата (рис.4).
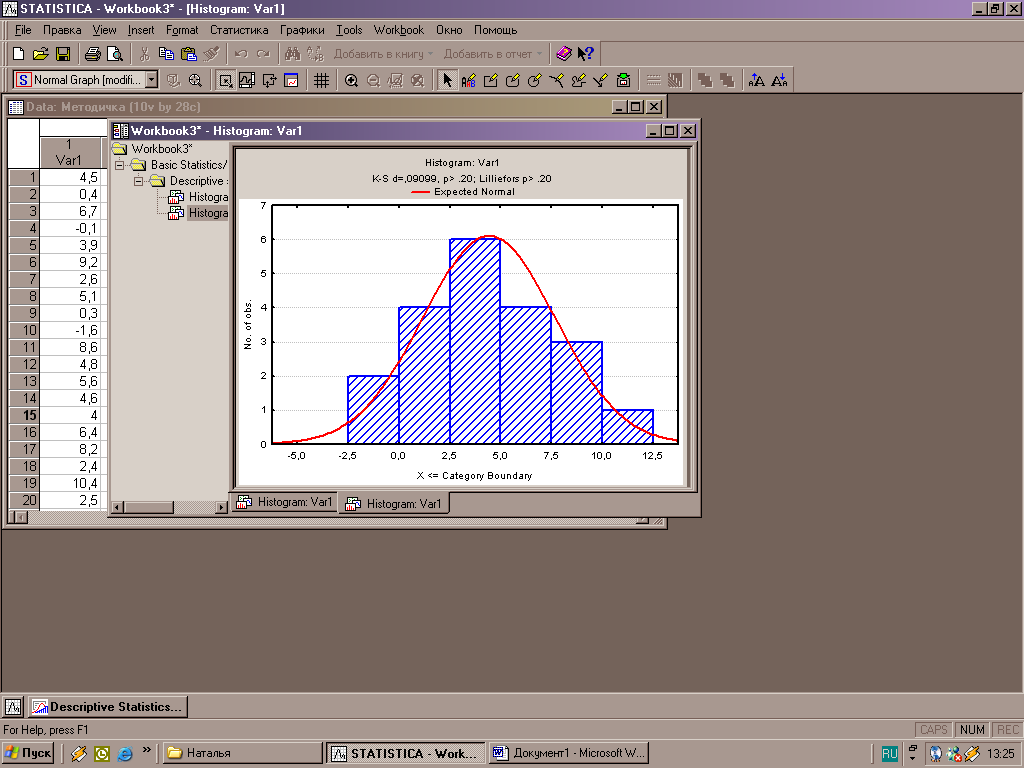
Рисунок 4 – Вывод результатов построения гистограммы
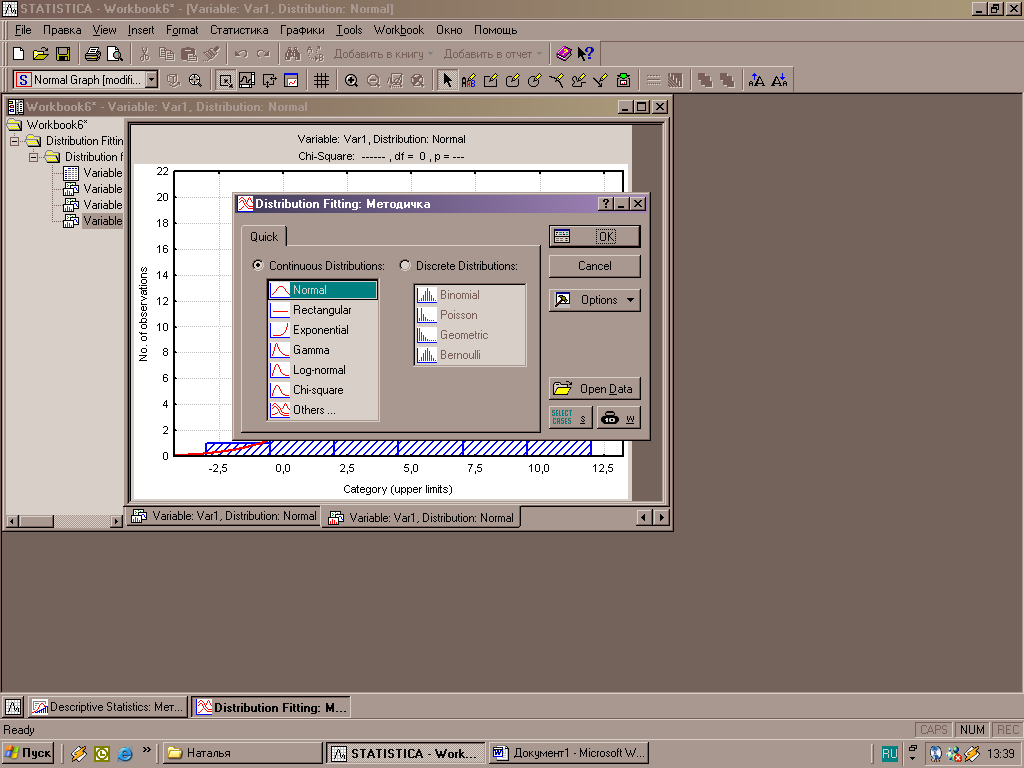
Рисунок 5 – Окно меню «Настройка распределения»
Для построения Функции распределения в меню «Статистика» выбирают функцию «Настройка распределения» (рис.5). После выбора вида распределения (на примере – нормальный закон распределения) нажимают на кнопку «ОК», после чего появляется форма ввода данных (рис.6). Для построения графика функции распределения в опции – «Option» выбирают параметр Cumulative distribution и в опции Quick выбирают функцию Plot of observed and expected distribution. После чего выводится график функции распределения (рис.6).
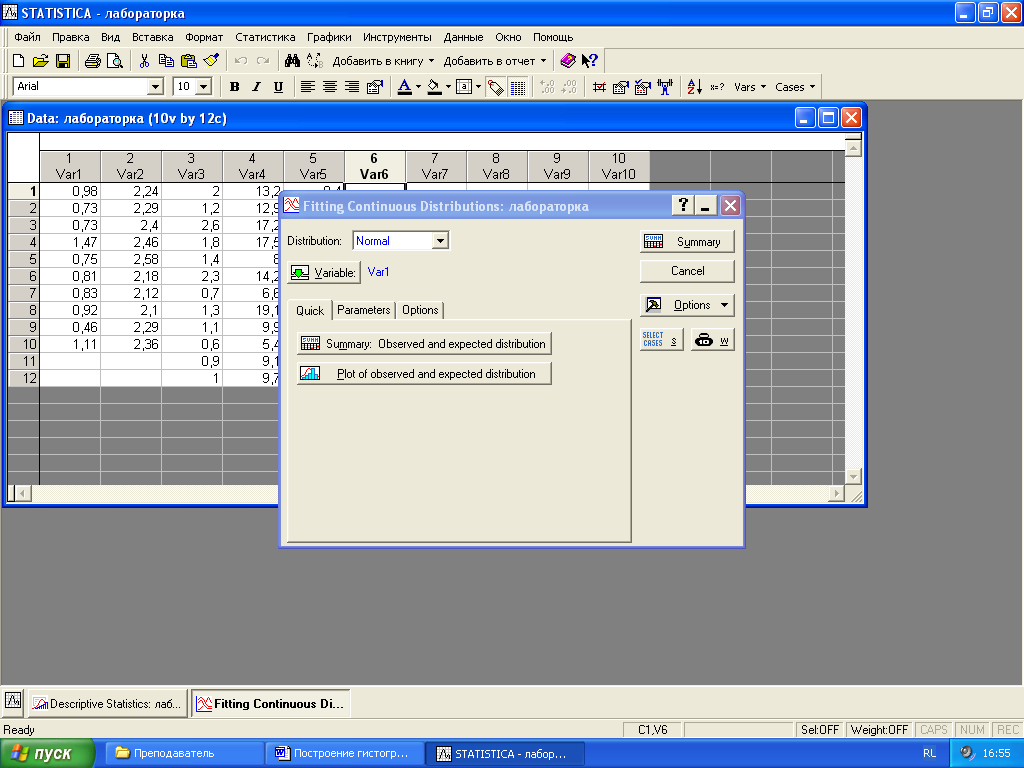
Рисунок 6 - ввод данных для построения функции распределения.
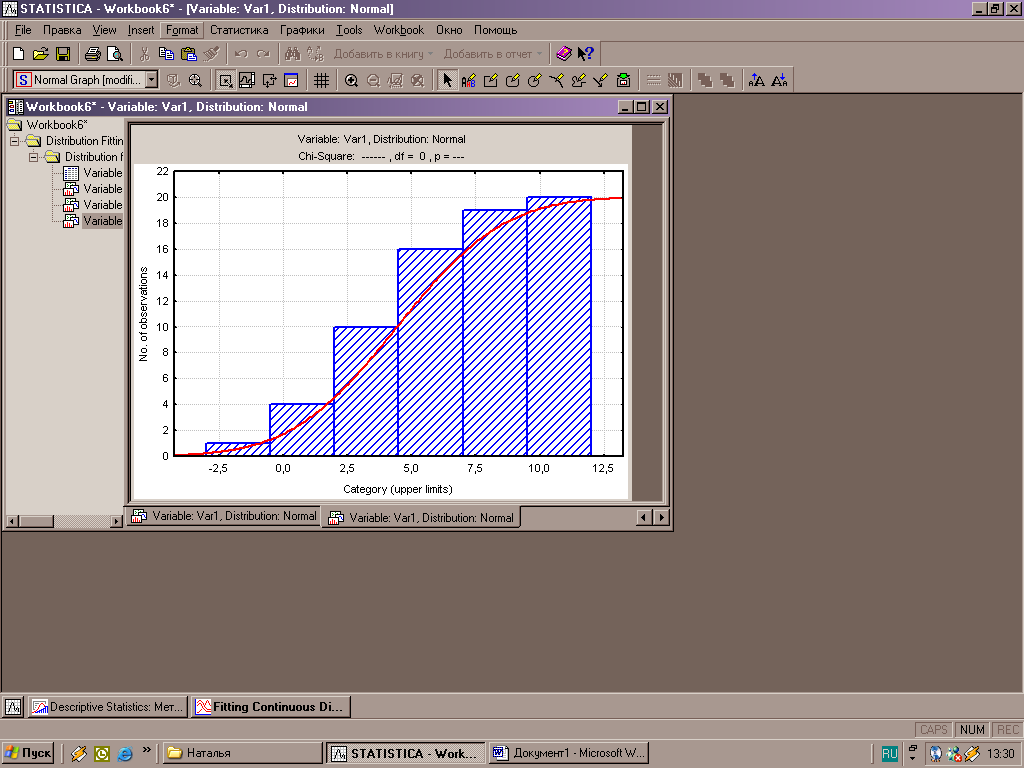
Рисунок 6 - Итоговое окно функции «Настройка распределения»
Построение гистограммы и функции распределения для переменной у (переменная 2) аналогично построению для величины х.
2 Проверка гипотезы о законе распределения генеральных совокупностей
Для проверки гипотезы о законе распределения также используют функцию «Настройка распределения» в меню «Статистика» (рис.5).
Для просмотра таблицы частот и их вероятностей необходимо нажать кнопку «Summary: Observed and expected distribution», для просмотра результата сглаживания статистического ряда служит кнопка «Plot of observed and expected distribution».
Сверху построенной гистограммы выводятся значения «Хи-квадрат» - распределения и вероятность принятия нулевой гипотезы. Если р>0,05, то гипотеза принимается, иначе – отвергается (рис.7)
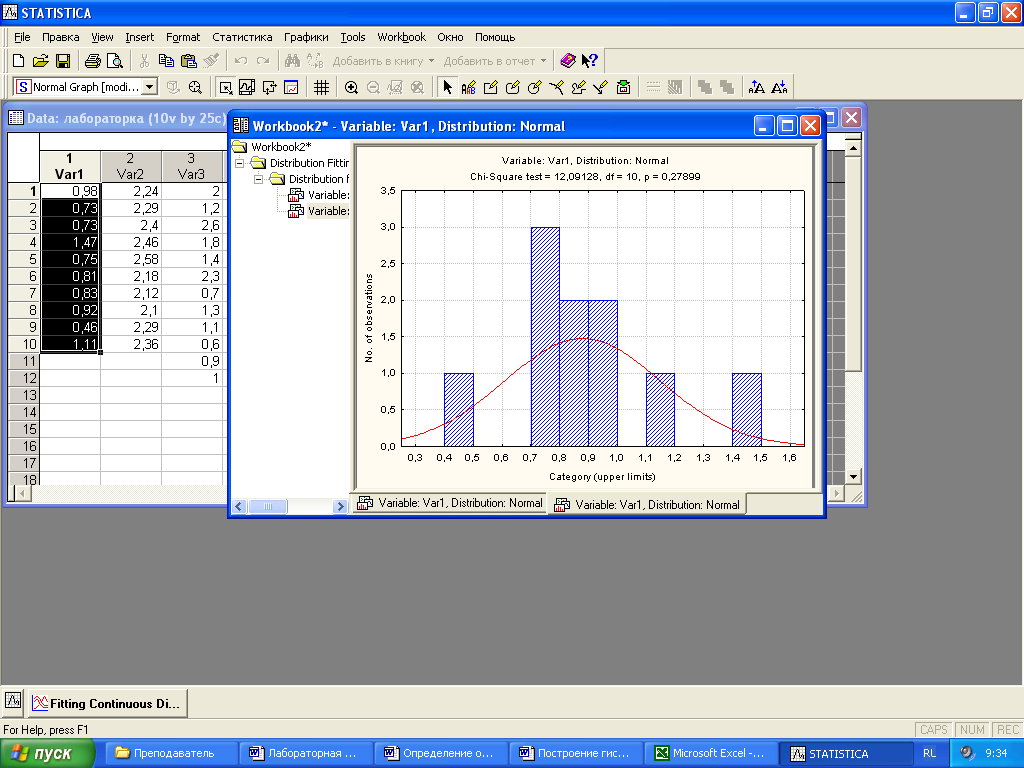
Рисунок 7 – сглаживание статистического ряда