2.2 Проверка гипотезы о нормальности закона распределения генеральной совокупности y

Ii	-0,4 1,34	1,34 3,07	3,07 4,82	4,82 6,56	6,56 8,3	8,3 10,04	10,04 11,78	11,78 13,5
mi	2	5	4	1	3	2	2	1

Среднее арифметическое

Точечная оценка дисперсии случайной величины Y:

Точечная оценка среднего квадратического отклонения

0,09

0,11

0,12

0,13

0,12

0,12

0,08

0,05

Вычисляем =1,76

Наблюдаемое значение также попадает в интервал

и случайная величина Y подчиняется нормальному закону распределения на уровне значимости 0,05.

3. Проверка гипотез о значении генеральной средней нормально распределенной совокупности заданным величинам

3.1 Проверка гипотезы о значении генеральной средней случайной величины X

По условию m_0x=5,5

H₀ : m_x=m_0x

Для проверки гипотезы используем статистику:

Выбирается двусторонняя критическая область.

По табл. П2-распределение Стьюдента для уровня значимости =0,05 и числом степеней свободы =20-1=19 определяем U_a=2,093

,

следовательно нулевая гипотеза отвергается.

2. Проверка гипотезы о значении генеральной средней случайной величины Y

По условию m_0y=6

H₀ : m_y=m_0y

Используем статистику:

По табл. П2 определяем U_a=2,093

,

Нулевая гипотеза отвергается на уровне значимости 0,05.

4 Проверка гипотезы о равенстве генеральных дисперсий, заданным величинам

4.1 Проверка гипотезы о равенстве генеральной дисперсии заданной величине случайной величины X

Используем статистику

Выбираем двустороннюю симметричную критическую область с границами, определяемым из условий

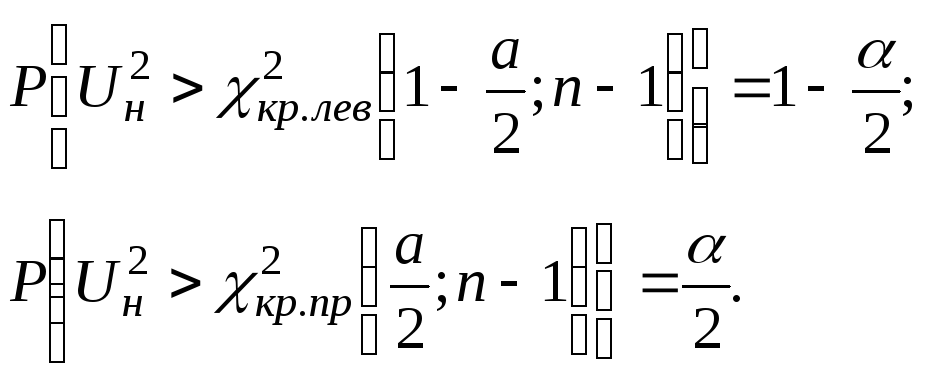
По табл. П 3 ² Пирсона находим ²_кр.лев для числа степеней свободы 20-1 и уровнем значимости

²_кр.лев=8,907

²_кр.пр для =19 и уровнем значимости ;

²_кр.пр=32,852

Т.к. 8,907<19,6<32,852 нулевая гипотеза не отвергается на уровне значимости 0,05.

4.2 Проверка гипотезы о равенстве генеральной дисперсии для случайной величины Y.

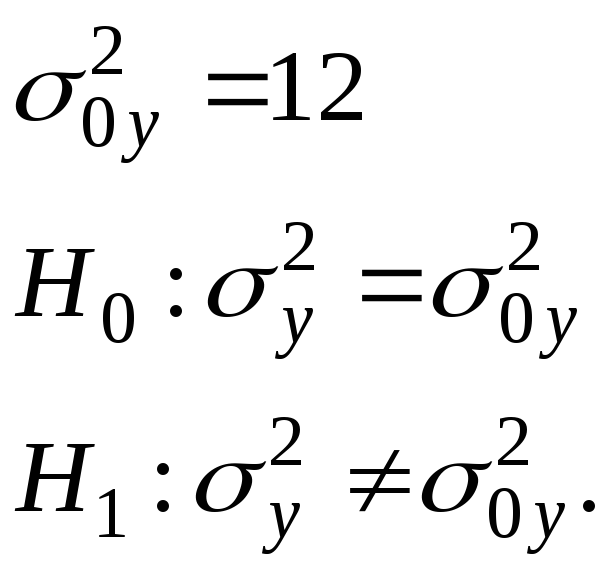
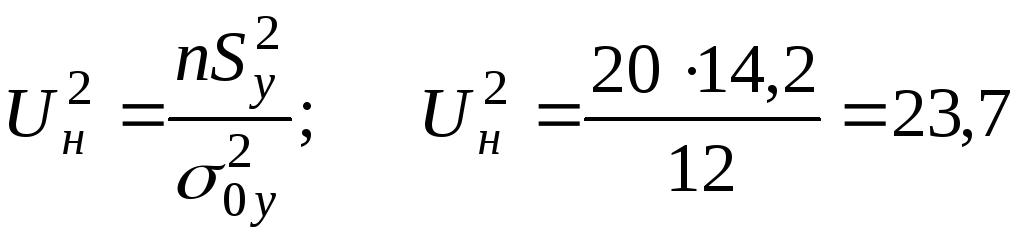
Аналогично п. 4.1

8,907<23,7<32,852 нулевая гипотеза принимается на уровне значимости =0,05.

5 Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей X и Y

Выдвигаем гипотезы:

Для проверки данной гипотезы используется статистика, имеющая распределение Фишера при справедливости Н₀:

Сравниваем полученное значение статистики с табличными значениями F_кр, найденное по табл. П.4 F-распределение с заданным уровнем значимости =0,05 и количеством степеней свободы в числителе k₁=n₁-1=19 и знаменателем k₂=n₂-1=19

2,11>0,92, F_кр>F_н, следовательно, гипотеза принимается.