Структурний синтез автомата Мура

Виконуємо структурний синтез мікропрограмного автомата Мура, заданого своєю таблицею переходів-виходів. Як приклад синтез виконуватимемо по зворотній таблиці (табл. _____).

1. У початковому автоматі кількість станів М=7, отже число елементів пам'яті m = ] log 2 M [ = ] log 2 7 [ = 3.

Нехай для синтезу використовуються D–тригери.

2. Кодуємо внутрішні стани автомата, використовуючи алгоритм кодування для D–тригерів. Кількість переходів в даний стан легко визначається із зворотньої таблиці:

а₁ ~ 2, а₂ ~ 3, а₃ ~ 2, а₄ ~ 1, а₅ ~ 1, а₆ ~ 1, а₇ ~ 2.

Тому коди станів наступні:

а₂-000, а₁-001, а₃-010, а₇-100, а₄-011, а₅-101, а₆-110.

3. Будуємо структурну таблицю переходів-виходів автомата Мура.

аm	K(am)	as(Y)	K (as)	X	ФВ
a6 a7	110 100	a1(-)	001	1	D3 D3
a1 a2 a6	001 000 110	a2(y1y2)	000		-
a1 a4	001 011	a3(y3y4)	010	1	D2 D2
a3	010	a4(y1y4)	011		D2 D3
a2	000	a5(y2y3)	101		D1 D3
a2	000	a6(y4)	110		D1 D2
a3 a5	010 101	a7(y2)	100	1	D1 D1

Побудова таблиці виконується аналогічно автомату Мілі.

4. Вирази для функцій збудження виходять у вигляді суми творів а та х, де а – початковий стан, х – умова переходу.

або

5. Вирази для вихідних сигналів автомата Мура одержуємо, виходячи з того, що ці сигнали визначаються тільки внутрішнім станом автомата.

6. Для побудови функціональної схеми автомата як і у попередньому випадку використовуємо дешифратор станів. Схема представлена на рис. 8.

Зауваження

1. При синтезі мікропрограмних автоматів викладеним методом одержувані вирази для функцій збудження не завжди є мінімальними і в деяких випадках можуть бути спрощені. Зокрема, можна довизначити функції збудження на деяких наборах одиничним значенням (а не нульовим, як було раніше) і виконати всі операції склеювання. Наприклад, в синтезованому раніше автоматі Мілі таким чином можна набути значення k₁=1.

Рекомендується в цьому переконатися самостійно.

Для спрощення схем автоматів можна також заздалегідь спростити ГСА, зменшивши кількість вершин або вузлів методами, викладеними / /.

Автомат Мілі в перебігу такту зберігає свій стан і лише в кінці його переходить в нове. Поки автомат знаходиться в даному стані A_i він виробляє вихідні сигнали у = f (A_i, x), де х - сигнали, що подаються на вхід автомата протягом даного такту. У зв'язку з цим автомат Мілі може інтерпретувати мікропрограму коректно тільки в тому випадку, якщо для будь-якого переходу виконується умова незалежності логічних умов від результатів виконання мікрооперацій на даному переході.

Умова незалежності порушується, якщо на деякому переході з a_m в a_s під дією сигналу х з виробленням у_і, спостерігається функціональна залежність х = f(у_і). У такому разі виконання мікрооперації у_і може привести до зміни значення х і автомат, знаходячись в стані а_т, і, реагуючи на набір вхідних сигналів, сформує набір вихідних сигналів, нf відповідній мікропрограмі. Щоб уникнути цього, можна використовувати наступні способи:

1. запам'ятати значення сигналів х на проміжок часу, рівний тривалості такту;

2. ввести в автомат додаткові стани;

3. реалізувати автомат по схемі Мура.

Запам'ятовування значень сигналів х протягом такту здійснюється операційним автоматом за допомогою додаткових елементів пам'яті - тригерів. Інтерпретація мікропрограми автоматом Мура розглядалася раніше. Введення додаткових станів ілюструється рис. 10.

У початковому автоматі (рис. 10 а) є переходи з а_і в a_j під дією сигналів х і х з виробленням y₁ і y₂ відповідно і має місце х = f(y₁, y₂). Дійсно, введення допоміжних станів a_k і a_l дозволяє усунути можливу помилку у видачі вихідних сигналів. На переходах а_і a_k або а_і a_l вихідні сигнали не виробляються. Переходи а_і a_k або а_і a_l є безумовними з виробленням y₁ або y₂ відповідно. У такому разі зміна значення х, в результаті виконання мікрооперацій y₁ або y₂, не вплине на вихідний сигнал, що виробляється автоматом, оскільки на переходах а_і a_k або а_і a_l вихідний сигнал вже не залежить від х.

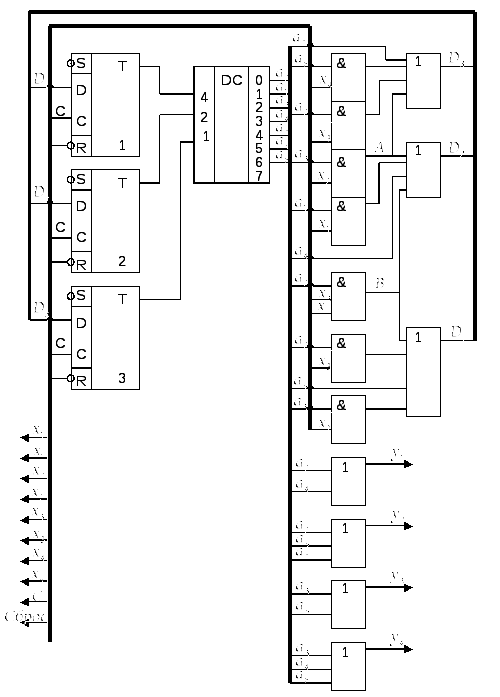
Рис. 9. Функціональна схема автомата Мура

Рис. 10. Введення додаткових станів в автомат Мілі: а) початковий автомат

б) автомат з додатковими станами.