Лабораторна робота №2

Тема.

Excel. Задача 2 «Прогнозування часових рядів з використанням регресійних моделей». Мета.

Уміти користуватися діапазонами клітинок і стандартними функціями, будувати різні види діаграм.

Задача 2 “ Прогнозування часових рядів з використанням регресійних моделей ”.

Освоїти технологію побудови регресійних моделей для прогнозування тчасових рядів в середовищі Excel

Теоретична частина.

Часовий ряд (ЧР) y(t) можна інтерпретувати у вигляді суми двох компонент – детермінованої складової f(t) і випадкового відхилення ε(t).

(1.1)

де y(t) - математична модель часового ряду, t – порядковий номер елементу ЧР, t=1,2, 3 ... n; n – число елементів ЧР.

У основі моделювання і прогнозування ЧР лежать операції ідентифікації (визначення) функцій f(t) і ε(t).Функція f(t) повинна мати такий вигляд, щоб сума квадратів відхилень ε(t) була мінімальною, тобто

(1.2)

При побудові детермінованої і випадкової складових моделі ЧР спочатку визначають загальний вигляд функцій f(t) і ε(t), а потім – їх коефіцієнти. Для визначення вигляду f(t) (інколи її називають трендом) найчастіше використовують наступні функції:

, (1.3)

, (1.4)

, (1.5)

де вираз (1.3) є поліном першого ступеня (лінійна залежність), (1.4) - поліном другої міри (параболічна залежність), а (1.5) - гіперболічна залежність. Вигляд тренда можна вибрати візуально по графічному відображенню y(t).

Припустимо, що графік y(t) має форму параболи. В цьому випадку приймається гіпотеза про параболічну залежність, тобто f(t) визначається по виразу (1.4). Тоді задача знаходження тренда формулюється таким чином: знайти значення коефіцієнтів а₀, а₁ і а₂ відповідно до виразів (31.2) і (1.4). Ця задача вирішується з використанням методу найменших квадратів (МНК) і інструментальних засобів Excel.

Після оцінки коефіцієнтів виробляють екстраполяцію детермінованої основи моделі. Під екстраполяцією розуміється процедура перенесення виводів, отриманих на ділянці спостереження, на явища, що знаходяться поза цією ділянкою. Припустимо, що відомі значення тимчасового ряду х_t в точках t₁<t₂<.,<t_n, які знаходяться усередині інтервалу (t₁, t_n) області визначення Т.

Екстраполяція – процедура встановлення значень ряду в точках, які лежать поза інтервалом t₁, t_n). Екстраполяція дає точкову прогнозну оцінку, обчислення якої здійснюється шляхом вирішення знайденого рівняння регресії f(t) для значення аргументу t_n+к, відповідного необхідному часу попередження t_n+к.

Наприклад, для параболічного тренда точкова оцінка детермінованої частини прогнозу y _n+к обчислюється таким чином:

(1.6)

Прогнозування випадкової компоненти ε(t) виконується методом авторегресії. Процесом авторегресії називається процес, значення якого в наступні моменти часу залежать від його ж значень в попередні моменти часу:

(1.7)

(1.8)

де b₁ – b_m - коефіцієнти рівняння авторегресії; m – порядок авторегресії, вирах (1.7) описує рівняння авторегресії першого порядку, а (1.8) – другого порядку; u(t) – помилка авторегресії.

Розрахунок коефіцієнтів b₁ – b_m також виконується методом найменших квадратів. Число змінних, що входять в модель авторегресії, називають порядком авторегресії.

Вибір порядку авторегресії є одним з етапів побудови моделі авторегресії. У даній роботі задається порядок авторегресії m=1. Побудову прогнозуючої моделі часового ряду рекомендується проводити в три етапи:

- побудова детермінованої частини моделі ЧР;

- побудова стохастичної частини моделі;

- визначення повного прогнозу ЧР на основі результатів двох попередніх етапів.

Хід роботи.

1. Побудова детермінованої частини прогнозуючої моделі ВР (етап 1)

А) Ввести вихідні дані ЧР (не менше 20 чисел) в стовпець A першого аркуша програми Excel, як показано на Рис. 1.

Б). Припустимо, що вихідний часовий ряд описується виразом 1.4. Для побудови параболічної залежності необхідно в стовпець B ввести нумерацію елементів ЧР t, а в стовпець С квадрат t, тобто t² (для побудови моделі поліноміальної залежності третьої міри в наступний стовпець вводяться дані t³ і т.д.).

В). Для обчислення коефіцієнтів моделі і додаткових результатів статистики в правій частині екрану за допомогою лівої кнопки миші виділити область порожніх вічок розміром 5х3 (5 рядків і 3 стовпці, кількість стовпців повинна відповідати кількості оцінюваних коефіцієнтів). Для отримання лише оцінок коефіцієнтів регресії виділити область розміром 1х3;

Г). Активізувати режим обчислення коефіцієнтів рівняння регресії в наступному порядку: “Вставка – Функція – Статистичні - Лінійн.- Ок».

Д). У вікні, що з'явилося, ввести наступні вихідні дані:

- Відомі значення_у – діапазон, що містить дані про об'єкт (виділити мишею стовпець даних ЧР);

- Відомі значення_х – діапазон, що містить дані часу і квадрата часу (виділити стовпці B і C);

- Константа – логічне значення, яке вказує на наявність або на відсутність вільного члена в рівнянні 1.6 (якщо вставити “1”, то вільний член a₀ розраховується, якщо -“0”, то вільний член дорівнює 0;

- Статистика – логічне значення, яке вказує, виводити додаткову інформацію по регресійному аналізу чи ні.

Щоб розкрити таблицю коефіцієнтів моделі, треба натискувати одночасно на комбінацію клавіш <Ctrl>+<shift>+<enter>.

Для введених вихідних даних: a₀= 4.2828, a₁= -0.032, a₂= 0.0023. Шукане рівняння регресії детермінованої частини моделі виглядає таким чином:

(1.9)

Е). Розрахувати модельні значення y_t в діапазоні t=1-20, підставляючи в отримане рівняння значення t і t² .

Всі дані в таблиці мають бути відцентровані, дробові числа закруглені до третього знаку після коми.

Результати розрахунків прикладу представлені на Рис. 1 в стовпці D (Yпр1).

Ж). Використовуючи графічні інструменти Excel, побудувати графіки вихідного ряду і ряду, розрахованого по виразу (1.9). Малюнок повинен мати назву, бути відформатованим по ширині аркуша, осі графіків мають бути позначені.

Порівняти графіки. Якщо вони сильно відрізняються, то можлива помилка в розрахунках. Написати висновок у звіт.

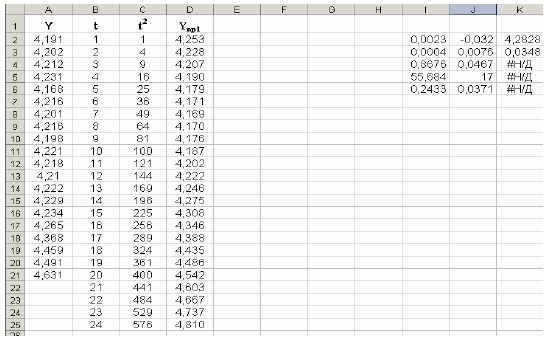
Рис.1- Приклад розрахунку коефіцієнтів регресії

2. Побудова стохастичної частини моделі ЧР (етап 2)

А). Для кожного спостереження ряду в стовпці E розрахувати відхилення ε(t), як різниця між відповідними даними стовпців A і D так, як показано на Рис. 1.2.

Б). Для визначення коефіцієнта b₁ рівняння (1.9) розташуємо в розрахунковій таблиці дані випадкової компоненти так, як показано в стовпці F на малюнку 1.2.

В). Визначити коефіцієнт b₁ моделі авторегресії, для цього повторити пункти В-Г етапу 1 з урахуванням того, що в даному випадку визначаються коефіцієнти рівняння першого порядку. У вікно вихідних даних вставити наступні значення:

- Відомі значення_у – виділити мишею діапазон комірок E3-Е21;

- Відомі значення_х – виділити мишею діапазон вічок F3- F21.

У комірці I9 представлено розрахункове значення коефіцієнта b₁= 0.6257. В результаті розрахунків методом найменших квадратів рівняння авторегресії першого порядку має вигляд:

ε (t) = 0.6257ε (t −1). (1.10)

Рівняння (1.10) побудоване без вільного члена b₀.

Г). У стовпці G розрахункової таблиці по виразу (1.10) розрахувати модельні значення випадкової компоненти для t=2,3,4...,21.

Д). Використовуючи вираз (1.10), у комірках G23- G 25 розрахувати прогнозні значення випадкової компоненти для t=22,23,24. При обчисленні ε (22) у комірці G23 використовувати значення ε (21) з комірки G22, при обчисленні ε (23) у комірці G24 використовувати значення ε (22) з комірки G24 і так далі.

3. Розрахунок оцінок повного прогнозу (етап 3)

Даний етап здійснюється по виразу (1.1) для t=21,22,23,24 у комірках H22-Н25 за даними комірок D22 і G22, D23 і G23, D24 і G24, D25 і G25.

За результатами розрахунків, представлених в колонках A, D і H побудувати графіки початкового ЧР, прогнозу на основі детермінованої моделі і графіка оцінок прогнозу з врахуванням випадкової компоненти.

На Рис. 2 для вибраного прикладу ці графіки позначені як Y, Y_пр1 і Y_пр2. Як видно з малюнка, графік Y_пр2 ближчий до графіка Y, що свідчить про підвищення точності прогнозних оцінок при обліку випадкової компоненти.

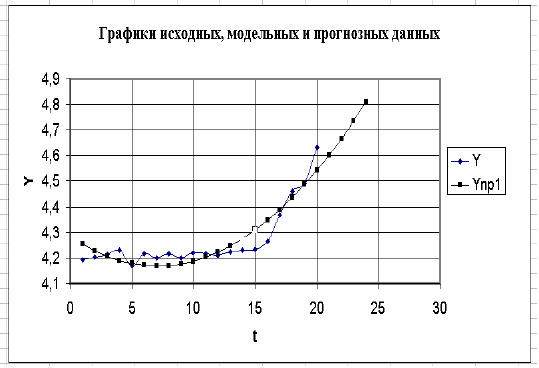
Рис.2 – Графики детермінованої частини прогнозуючої моделі ЧР

Для свого варіанту виконати аналіз графіків, отриманих в результаті виконання завдання, та записати висновок у звіт.

Контрольні запитання

1. Що таке копіювання формул?

2. Наведіть приклади відносних адрес клітинок?

3. Наведіть приклади абсолютних адрес клітинок?

4. Що таке діапазон клітинок?

5. Як виокремити діапазон?

6. Як вилучити рядок з таблиці?

7. Яке призначення приміток?

8. Який пріорітет виконання операцій в формулах?

9. Що зображено в клітинці після введення в неї формули?

10. Які є режими відображення результату роботи формул у комірках?

11. Які є категорії стандартних функцій?

12. Наведіть приклад прямокутного діапазону?

13. Наведіть приклади статистичних функцій?

14. Як відцентрувати заголовок таблиці відносно стовпців?

15. Яке призначення кнопки АВТОСУМА?

16. Які математичні функції є в ЕТ?

17. Яка різниця між абсолютними і відносними адресами?

18. Яким символом відокремлюють аргументи у функціях?

19. Як задати режим відображення формул?

20. З чого будують символи у формулах?

21. Навести приклади економічних і технічних завдань, де потрібні прогнозні оцінки.

22. Дати характеристику моделі прогнозу.

23. Як вибираються моделі детермінованої і стохастичної складової прогнозу?

24. Описати процес визначення коефіцієнтів моделі в середовищі Exсel.

25. Чим відрізняються процедури інтерполяції і екстраполяції ЧР?

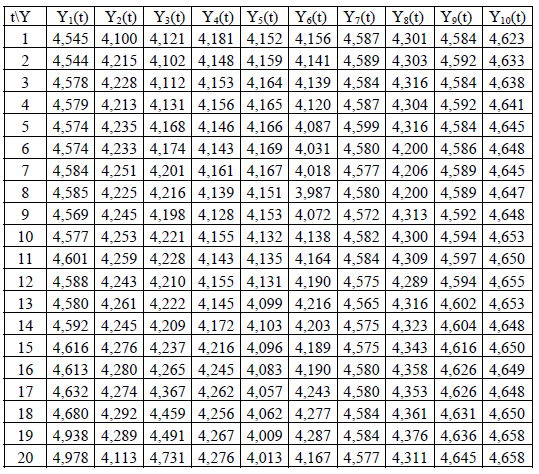
Варіанти завдань

По стовпчикам наведено різні варіанти у вигляді часових рядів Y₁, Y₂, Y₃ і т.д.