Термодинамика Элементы статистической физики.

Вероятность:

При подбрасывании монеты раз вероятность выпадения орла или решки приближается к

Игральные кости:

; ; ; … ; ;

; Вероятность невозможного события равна нулю.

Вероятность достоверного события равна единице.

; ;

- формула сложения вероятностей.

; .

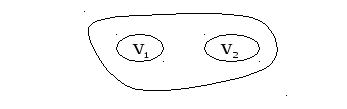
Вероятность нахождения частицы в этих двух объемах:

Лекция № 15

;

- функция распределения случайной величины (вероятности).

Пример. Игральные кости

; ; ; ; ;;

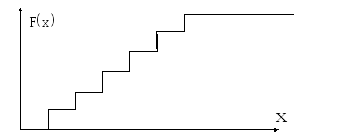
Пример. Циферблат часов

;

Таким образом, функция примет вид:

изменяется до

- плотность вероятности.

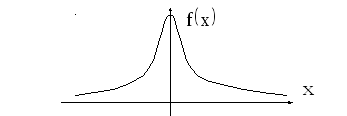
Распределение плотности вероятности(распределение Гаусса)

Рассмотрим систему случайного движения точки в плоскости .

Из точки О скачками движется частица. Каждый шаг –равновероятен по всем направлениям, а его величина распределена по произвольному закону. Шаги независимы. Задача-получить распределение координат точки после большого числа шагов. Поскольку движение по обеим координатам независимы, смещения в положительном и отрицательном направлениях равновероятны. Чтобы исключить влияние направления рассматривается зависимость от квадрата координаты.

Плотность вероятности для точки иметь координату х зависит от х², т.е. равна φ₁(x²), аналогично для y φ₂(y²). Вероятность нахождения точки в элементе площади dxdy с координатами x и y равна

dp = φ₁(x'²)φ₂(y²)dxdy

При повороте системы координат, так, чтобы ось x' прошла через элементарную площадку. При этом связь координат имеет вид

x'² = x² + y²

При этом вероятность нахождения точки в элементе площади dxdy с новыми координатами равна

dp = φ₁(x'²)dxdy

Это одна и та же величина поэтому можно записать

φ(x'²) = φ₁(x'²)φ₂(y²) = φ(x² + y²) – функциональное уравнение

Решаем функциональное уравнение используя свойства и структуру уравнения. Для этого логарифмируем это уравнение

;

Дифференцируем полученное выражение по x² , и по y²

;

;

;

;

;

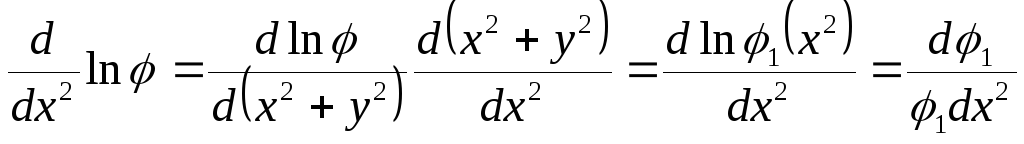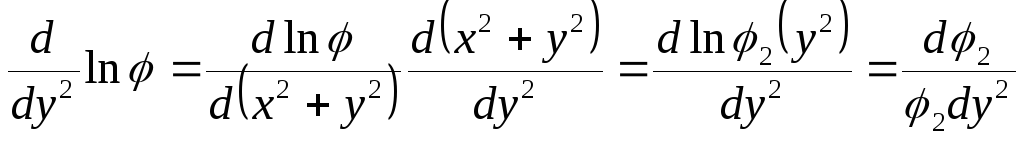Распределение Гаусса.

Доска Гальтона.

………………………….

………………………….

………………………….

………………………….

………………………….

………………………….

………………………….

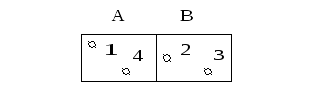
Назовем микросостоянием заданные состояния всех молекул.

Макросостояние – состояние при заданных макропараметрах. , число молей и т.д.

Макросостояние реализуется различными способами или микросостояниями.

Число микросостояний, характеризующих данное макросостояние, называется статистическим весом макросостояния.

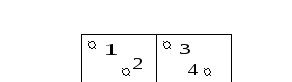
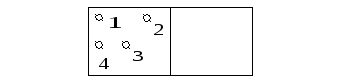
Вероятность пребывания 1 молекулы в части А(поскольку равновероятно в А или в В – вероятность пребывания в А равна ½)

Вероятность одновременного пребывания в А двух молекул равна произведению ½ *1/2 (события независимы)

Вероятность одновременного пребывания в А 4-х молекул равна (1/2)⁴ =1/16.

Поскольку вероятность попадания в объем пропорциональна объему, то

Р(V_A) =V_A/( V_A + V_B) – вероятность попадания молекулы в объем А.

Р₁(V_A) =(V_A/( V_A + V_B))^N –вероятность попадания N молекул в объем А.

Р₂(V_B) =(V_B/( V_A + V_B))^N – вероятность попадания N молекул в объем В.

Возможные распределения молекул по половинкам А и В

Способы реализации системы макросостояний		Число способов-реализаций состояния	Вероятность события
A	B	Г	p
-	1234	1	1\16
1 2 3 4	234 134 124 123	4	1\4
12 13 14 23 24 34	34 24 23 14 13 12	6	6\16
123 124 134 234	1 2 3 4	4	1\4
1234	-	1	1\16

; ; ; ; ; ;

;

, где - количество частиц.

макросостояниях

Статистический смысл энтропии

Запишем для энтропии

;

Поскольку из уравнения состояния идеального газа для одного моля следует

;

Перепишем уравнение для энтропии

;

Или интегрируя

При постоянной температуре

;

Изменение энтропии логарифмически зависит от объема или точнее от отношения объемов

;

;

Поскольку число микросостояний пропорционально объему

- энтропия –логарифм числа микросостояний -формула Больцмана.

- уравнение Больцмана.

Чем более упорядочена система, тем меньше число микросостояний, характеризующих данное макросостояние.

Если все атомы закреплены в определенных местах, тогда существует единственное микросостояние и энтропия равна нулю.

Состояние с максимальной энтропией является наиболее вероятным состоянием.Энтропия –мера разупорядоченности(беспорядка, хаоса) системы.

В состоянии равновесия энтропия максимальна и это состояние наиболее вероятно.

Если система предоставлена сама себе, то она будет стремиться к равновесию.

Плотность вероятности(объемная интерпретация)

Объем разбивается на части V_i. Вероятность нахождения частицы в объеме ∆V_i

P(∆V_i) = lim_N->∞ (N_i/N)

N_i - число испытаний, когда частица обнаружена в объеме ∆V_i , N – общее число испытаний

Плотность вероятности

Вероятность нахождения молекулы в бесконечно малом объеме, отнесенная к объему.

f(x,y,z) = lim_∆V->0 P(∆V_i)/∆V_i = lim_{∆V->0 N->∞} (N_i/(∆V_iN)) – вероятность нахождения молекулы в бесконечно малом объеме, отнесенная к объему.

По аналогии с плотностью вещества

ρ= lim_∆V->0 (∆m/∆V)

Если провести N₀ наблюдений, то в объеме ∆V в окрестности точки x,y,z молекула будет обнаружена в

dN = N₀f(x,y,z)dV = N₀f(x,y,z)dxdydz

случаях. В конечном объеме V₁ – молекула окажется обнаруженной

N(V₁) = N₀ ∫_V1f(x,y,z)dxdydz - раз.

Вероятность P((V₁) быть обнаруженной при наблюдении в объеме V₁ для молекулы

P((V₁) = N(V₁)/N₀ =∫_V1f(x,y,z)dxdydz

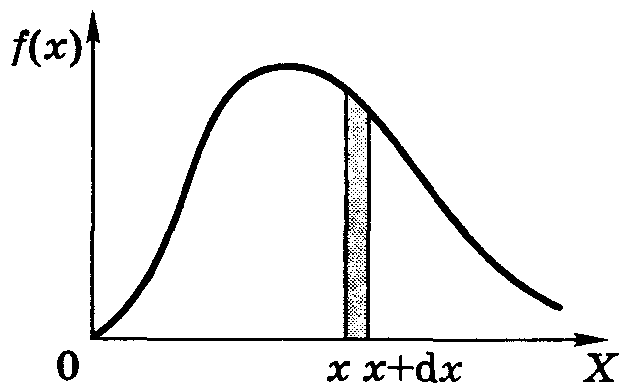
В пределе получим условие нормировки

P((V₁->∞) = N(V₁->∞)/N₀ =∫_V1->∞f(x,y,z)dxdydz =1 – условие нормировки плотности вероятности

Для замкнутого объема

∫_VfdV=1

Если положения молекулы равноценны, то f₀ =const. Из условия нормировки следует

∫_Vf₀ dV=1 =f₀V=1

Тогда

f₀=1/ V

в этом случае

N(V₁) =N₀ ∫_V1f₀dV = N₀ V₁/V

P(V₁) = N(V₁) /N₀ = V₁/V(что справедливо для постоянной плотности вероятностей)

Сложение вероятностей независимых событий

P(V₁+V₂) = (V₁+V₂)/V = V₁/V+V₂/V = P(V₁)+P(V₂)

Что интерпретируется как или в объеме V₁ или в объеме V₂. Объемы или множества непересекающиеся.

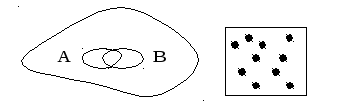
В общем случае при зависимости событий

P(A+B) = P(A) +P(B) - P(AB)

Где

P(AB) = N_AB/N

В объемной интерпретации

P(V₁+V₂) = (V₁+V₂ –V₁₂)/V = P(V₁)+P(V₂) –P(V₁₂)

Условная вероятность

Условная вероятность – это вероятность события A при условии, что произошло событие B – обозначается как P(A/B). Например, вероятность вытащить белый шар из урны при условии, что вытащен черный шар.

Поскольку общее число исходов испытаний при которых произошло событие B, равно N_B а из него в N_AB случаях произошло событие A, то

P(A/B) = N_AB/N

Переходя на континуальное рассмотрение условная вероятность P(V₁/V₂) нахождения частицы в объеме V₁ в случае если она находится в объеме V₂ , сводится к вычислению вероятности нахождения частицы в объеме V₁ , в случае, если она находится в объеме V₂, поэтому

P(V₁/V₂) =V₁₂/V₂

Преобразуем

P(A/B) = (N_AB/N)/(N_B/N) = P(AB)/P(B)), P(AB) – вероятность совместного наступления событий A и B.

Тогда

P(AB) = P(B) P(A/B) = P(A) P(B/A) – формула умножения вероятностей

Для независимых событий

P(A/B) = P(A)

P(AB) = P(A) P(B)

Вероятность микросостояния

Р_а = Г_а/Г₀

Г_а – число микросостояний –термодинамическая вероятность

Г₀ – общее число состояний, достижимых для системы

Формулы комбинаторики

Теория размещений

Задача 1

n -мест, n - различных предметов

Число способов размещения n предметов по n местам!

Один предмет –на n мест - n способов

Второй предмет на оставшиеся n -1 мест –поэтому 2 предмета n(n -1) –способов

3 предмета n(n -1)(n-2) способов

n На n - n! способов n(n -1)(n -2)….1 = n!

На 3х стульях 3 человека 3! –способов

Задача 2

m -различных предметов, n - мест

Число способов размещения m предметов по n местам!

Если разместить m предметов, то n-m мест свободны

Если бы эти n –m мест были бы заняты различными предметами, то при каждом фиксированным раcположении m предметов их можно было бы разместить (n -m)! Способами. Если перебрать все возможные размещения m по n местам и при каждом из них произвести (n -m)! Размещений n-m других предметов на оставшихся n - m местах, то всего получается число различных размещений m+(n - m) = n различных предметов по различным местам, т.е. n!

Следовательно, искомое число способов размещения m предметов по n различным местам

Р(n, n - m) = n!/(n - m)!

|∆□_ |□_∆ | _∆□ | ∆_□ |□∆_ | _□∆|

Задача 3

m По n, но m -одинаковые и неразличимые

|∆∆_ |∆_∆ | _∆∆|

Размещения, когда поменялись местами два предмета считаются одинаковыми. В этом случае при каждом размещении предметов можно произвести ! перестановок, которые не изменят размещения. Следовательно, искомое число способов

C(n,m) = n!/[m!(n-m)!]

Задача 4

Сколько способов выбора!

n - различных предметов, m - предметов, отличающихся по составу( n- вагонов m - студентов)

∆□○ n=3 m=2

|∆□|∆○|□○|

Если предмет в группе 1, то n -способов, если 2, то n(n-1) -способов, каждый из различных предметов комбинируется с (n-1) оставшимися.

Комбинации, отличающиеся лишь порядком, одинаковы. Число перестановок для 2-х 2! И тогда n(n-1)/2!

Для m

C(n,m) =

Расчет вероятности макросостояния

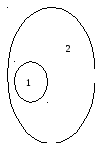N,V,n

1- N₁, V₁,m

2-N-N₁, V- V₁,n-m

V – объем идеального газа

n-число частиц диаметром d в этом объеме V₁ находится n -частиц

N = V/d³ Где d³ ≈10^-30m³

Всегда соблюдается условие N>>n

Вероятность макроскопического состояния системы, при котором в объеме V₁ m -

V₁ содержит ячеек больше чем m

N₁ = V₁/ d³ , поэтому N₁ ≥ m

Общее число микросостояний равно, числу способов которыми можно разместить n -частиц по N ячейкам. Предполагается, что частицы отличаются друг от друга(пронумерованы). Свойства частиц одинаковы и если обмен частицами произошел, то состояние не поменялось, но микросостояния различны !!!!

Число микросостояний Г₀ = N!/(N-n)!

Число микросостояний, посредством которых реализуется макросостояние, когда в объеме V₁ имеется m каких-то частиц

g(V₁, m) = N₁!/(N₁ -m)!

В остальной части объема V - V₁ содержится n-m остальных частиц. Число микросостояний для них

g(V - V₁, n-m) =(N-N₁)!/[N-N₁ –(n-m)]!

Т.о. для конкретных частиц в объеме V₁ общее число микросостояний

g(V₁, m)g(V - V₁, n-m), поскольку каждое микросостояние в V₁ комбинируется со всеми состояниями в V -V₁. но произведение не дает всех микросостояний поскольку это только для некоторого набора m -частиц в объеме V₁. но m частиц из общего числа n частиц можно выбрать n!/[m! (n-m)!] Способами. Поэтому общее число микросостояний

Г(V₁, m) = g(V₁,m) g(V - V₁, n-m)

Следовательно, вероятность макросостояния

Р(V₁, ) = Г(V₁, )/Г₀ =

Для газа при нормальных условиях V=1см³, n≈10¹⁹ , N≈10²⁴, N₁ =10²⁴(V₁ /V)

При этом N₁ >>m

ln n! = ln1 + ln2 + ln3 + ….lnn = ∑_1,nlnn∆n, ∆n = 1

ln n! ≈∫₁ⁿ lnndn = nln n – n, 1 n→∞ ∆n → 0

n! =e^nlnn-n = e^nlnne^-n =nⁿ/eⁿ = (n/e)ⁿ

Преобразуем формулу вероятности макросостояния с использованием формулы Стирлинга

N>>m, N – N₁ >> n-m, N>>n

Тогда

(N₁ - m)! = = =e^-m

Где учтено, что lim_n→∞ (1+x/n)ⁿ =e^x

Аналогично все факториалы, тогда

P(V₁, m) = =

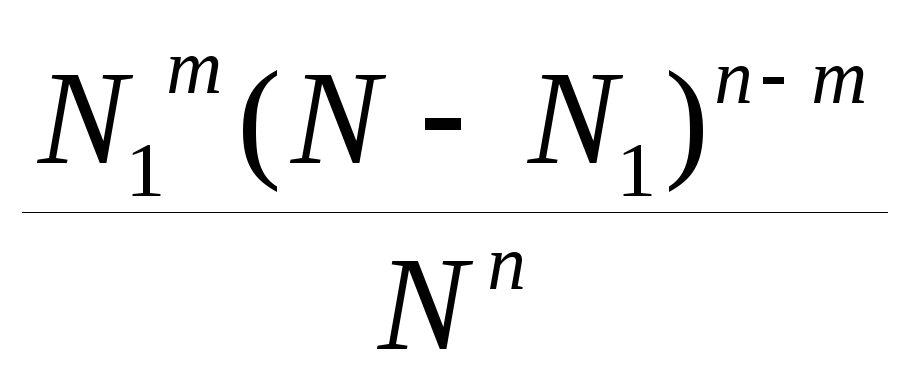Смысл формулы

Р = = - вероятность нахождения частицы в объеме V₁

_q=1-N₁/N = 1-p – вероятность нахождения частицы в остальной части объема V-V₁

Сумма вероятностей

p+q =1, поскольку частицы или в V₁ или в V-V₁

тогда для вероятности

P(V₁, m) = р^mq^n-m –биноминальное распределение

Физический смысл энтропии

Из первого закона термодинамики запишем

Поскольку

p/T = R/V

и, кроме того,

dT/T = dlnT dV = dlnV

дифференциал энтропии запишем

dS = d(c_vlnT + RlnV), причем для изотермы T=const

имеем

dS = RlnV

или

∆S=lnV₂/V₁

Число частиц в 1 моле – это число Авогадро N_A

Число состояний системы

Г₀₁ =

Г₀₂ =

Где N₁ = V₁/l³ , N₂ = V₂/l³

_l =10^-10 m - размеры частиц

Используя формулу стирлинга

= ≈

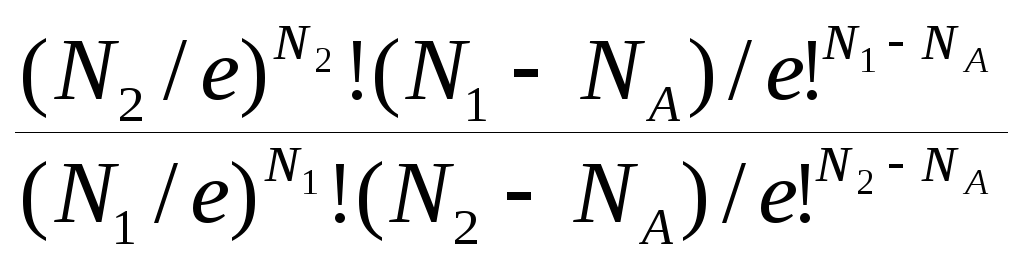
Для разреженного газа

N₁ >>N_A , N₂ >>N_A

Тогда приближенно но с большой точностью

= =

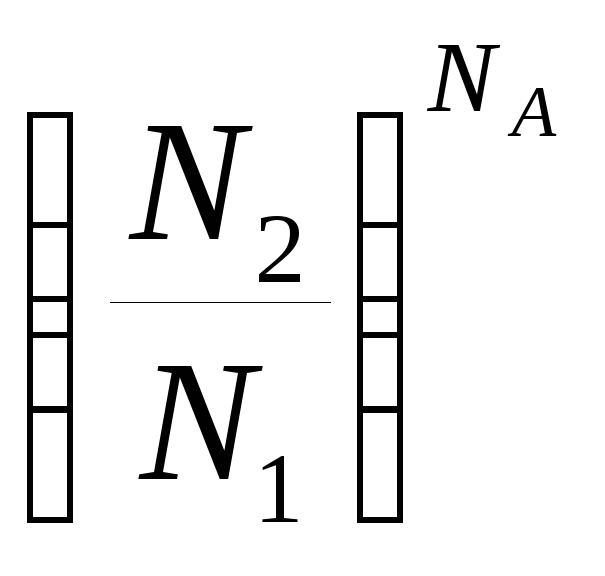∆S =S₂ – S₁ = = kln Г₀₂ -kln Г₀₁

R/N_A = k –

Таким образом энтропию можно интерпретировать как логарифм числа микросостояний

S = kln Г –формула Больцмана

Чем более упорядочена система, тем меньше число микросостояний, которыми реализуется макросистема. Если все атомы закреплены в определенных местах, тогда существует одно микросостояние, а соответственно, энтропия равна 0. чем больше микросостояний Г->0, тем более разупорядочена система. Энтропия – мера разупорядоченности(беспорядка, хаоса) системы.

В состоянии равновесия S -max, наиболее вероятное состояние.

Система, предоставленная самой себе движется к равновесию.

Все процессы в природе стремяться к равновесию.

Тема: распределение Максвелла – Больцмана

Физическое содержание вопроса: молекулы хаотически движутся, для них характерен вероятностный подход

Цель: получить зависимость доли частиц, имеющих скорости в диапазоне от м до м+ вм(вероятность)

Задачи, вытекающие из цели: 1.выразить вероятность

2. проинтегрировать

3.проанализировать

4.практически применить

Метод решения: решение функциональных уравнений(логарифмируя и дифференцируя, затем интегрируя полученную зависимость путем сведения к произведению интегралов и переходу к полярным координатам

2-й метод- переход к сферическому слою

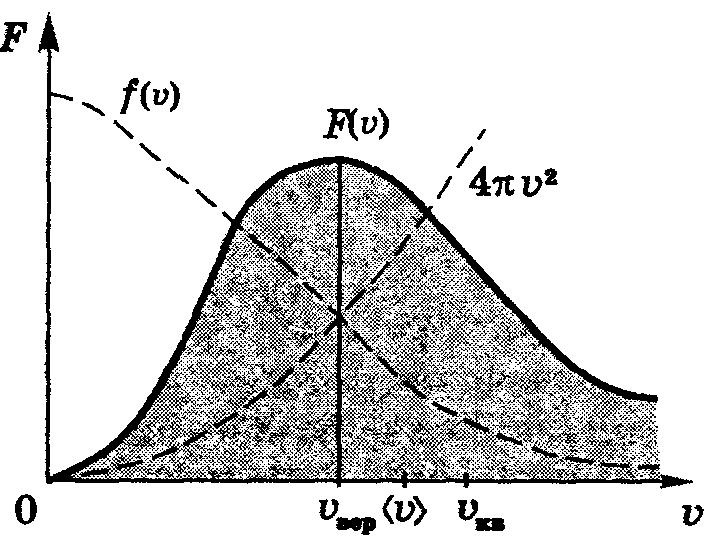
Выводы: график, есть максимум. Есть крылья. Можно получить наиб вероятную скор., ср скор., ср квадратичную скор.

Практические примеры: расчет доли молекул в диапазоне наиб вер скор

Распределение Максвелла.

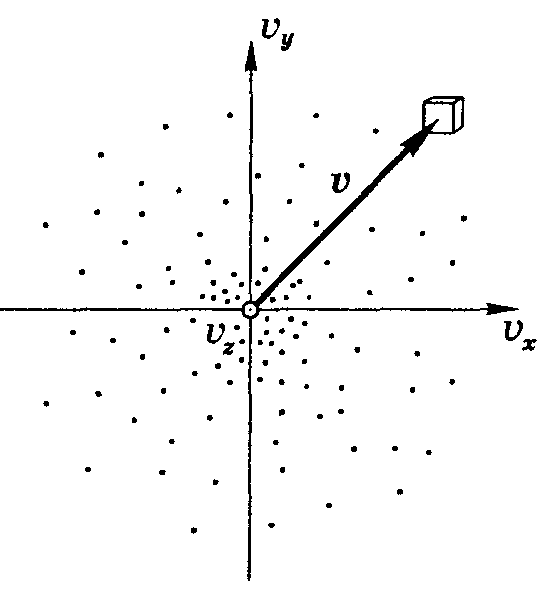
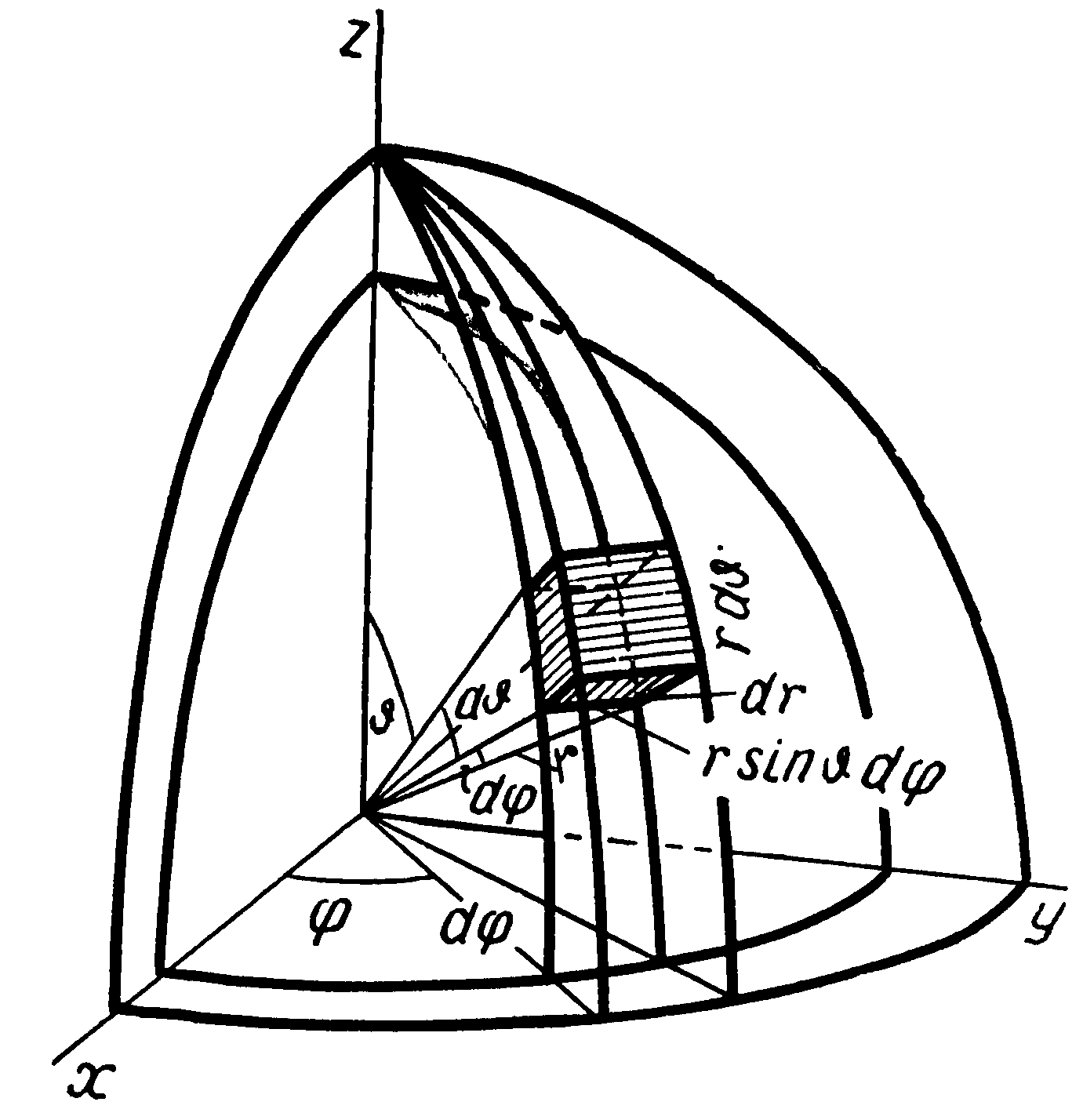
Из Бурштейна

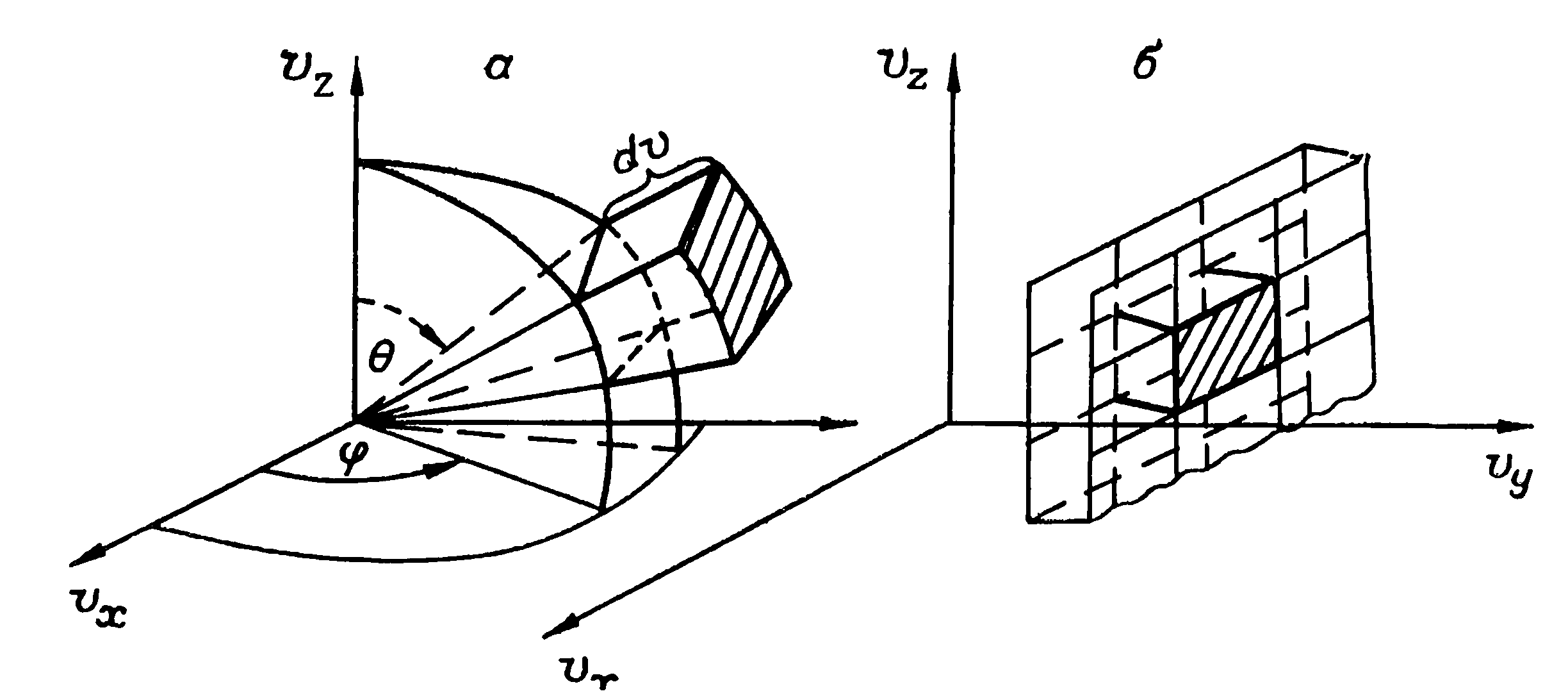
Иродов

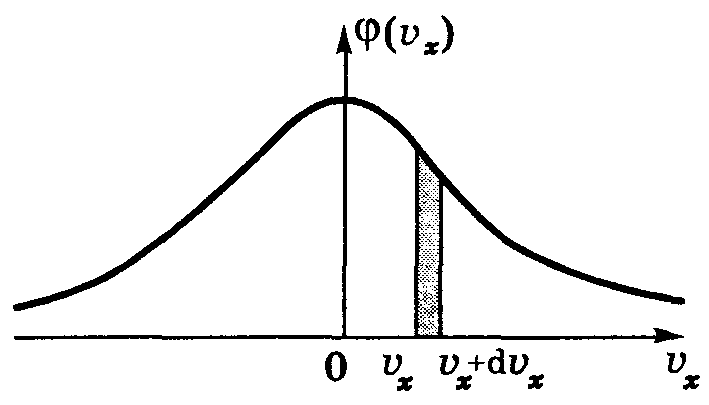
до

Получить функцию распределения вероятности молекул по скоростям.

Допущения при выводе формулы:

1. скорости молекул равновероятны, имеют различные значения

скорости молекул равнонаправлены по всем координатам при различных значениях.

2. составляющие скорости независимы.

- вероятность того, что молекула имеет скорость в пределах от до

выражается через плотность распределения в виде

Аналогично для другой координаты

Аналогично для 3-ей координаты

Вероятность одновременного попадания трех компонент скорости в соответствующий интервал

dω = ω₁ω₂ω₃

Вероятность зависит от квадрата скорости, чтобы знак скорости не влиял

Под квадратом вектора скорости понимается зависимость от компонент по формуле

;

С другой стороны

;

Или

;

Откуда следует функциональное уравнение

;

Логарифмируя

Решаем функциональное уравнение, дифференцируя по компонентам скорости

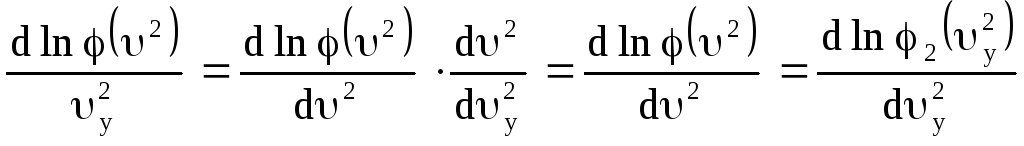
И т.д.

Учитывая, что производная от квадрата скорости по квадрату компонента скорости равна 1, и, следовательно, равны между собой покомпонентные производные, можно приравнять покомпонентные производные одной постоянной величине

;

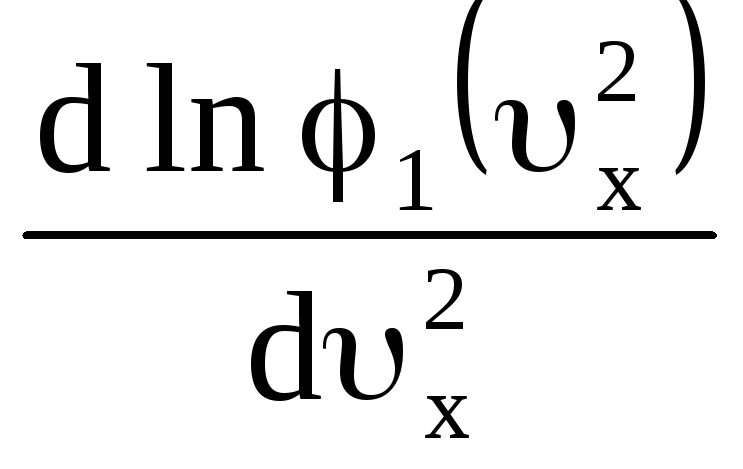
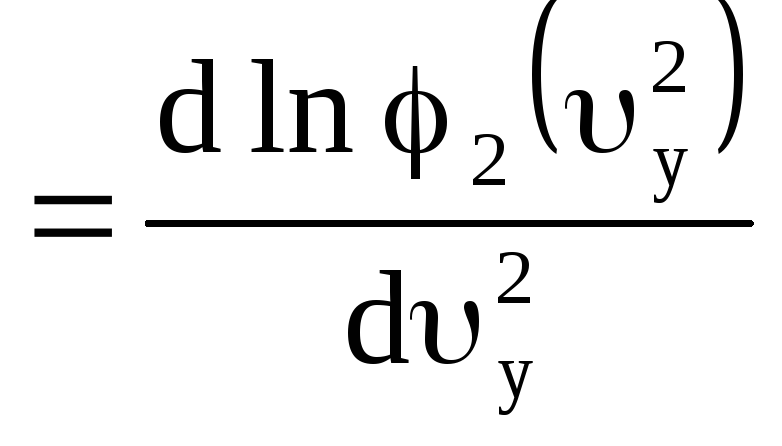Приравниваем постоянной эти уравнения

;

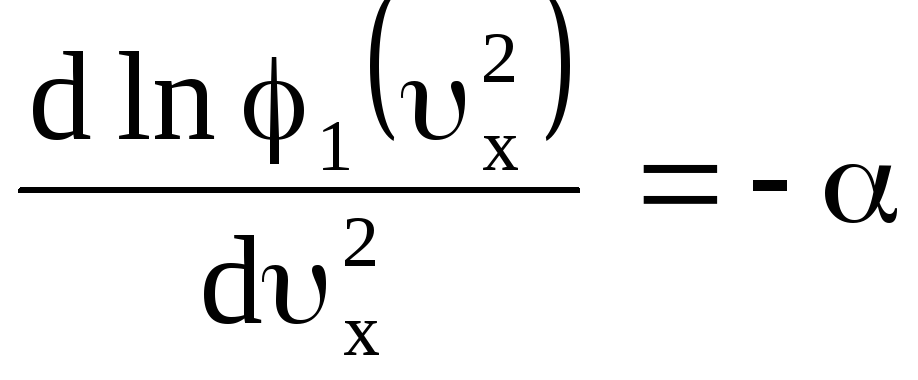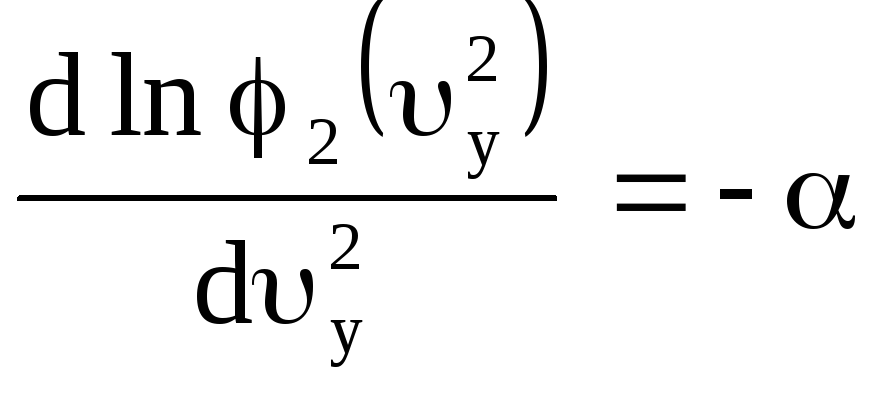
И т.д.

Тогда для плотности функции распределения справедливы равенства

;

;

Учтем условие нормировки.

Из него определяем константы.

условие нормировки

;

Причем, интегрирование выполняется по всем возможным значениям скорости.

Физический смысл условия номаровки – левая часть представляет собой вероятность того, что данная молекула будет иметь какое-нибудь(любое) значение составляющей скорости, а это событие является достоверным. Вероятность же достоверного события равна единице.

Для распределения условие нормировки дает

- интеграл Пуассона.

Интеграл в левой части – интеграл Пуассона.

Вычисляется он следующим образом. Рассмотрим интегралы

;

;

Так как значения определенного интеграла не зависит от обозначения переменной интегрирования, то интеграл 1 равен интегралу 2. поэтому:

Переход от декартовых координат к полярным дает возможность упростить вычисления. Площадь элемента в полярной системе координат:;

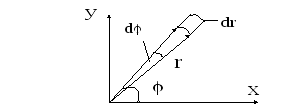
Отсюда, учитывая, что элемент площади выражается в полярных координатах

Учитывая равенство интегралов, перепишем

=

= = = =

Из условия нормировки следует

Здесь интегрировали по углу и использовали равенство

I==

Поскольку такие же значения имеют константы С₁ и С₂ , то постоянная перед интегралом равна

A=

На основании предыдущих зависимостей получим

Лекция № 16

Представляя элементарный объем в сферических координатах(рис ), где одна грань элемента v sinψ dφ , а другая v dψ и высота элемента dv для модуля скорости получим

v sinψ dφ

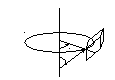v dψ

В сферических координатах

Вероятность обнаружения у любой выбранной молекулы какого-либо признака характеризует в то же время относительное число молекул, обладающим этим признаком, следовательно, можно определить относительное число молекул, конец вектора скорости которых лежит в заданном элементе объема, или, иными словами, относительное число молекул, имеющих заданную по величине и направлению скорость.

Если требуется определить вероятность обнаружения у некоторой молекулы скорости, заданной только по величине при любом ее направлении, т.е. по модулю скорости, то последнее выражение необходимо проинтегрировать по всем возможным направлениям углов, т.е.

Тогда получим

Или

;

Можно сказать, что величина

Представляет собой вероятность обнаружения конца вектора скорости в шаровом слое, заключенном между сферами с радиусами, отличающимися на приращение радиуса.

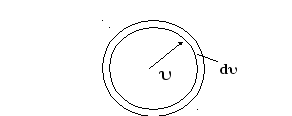
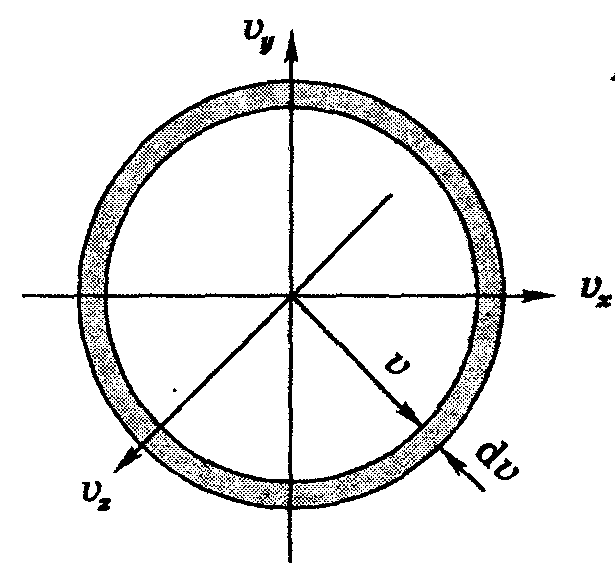
Для сферического слоя можно получить аналогичные результаты. Рассмотрим сферический слой

- сферический слой.

Объем сферического слоя равен произведению площади слоя на толщину слоя, равную разности скоростей

Или

;

Тогда функция распределения частиц по скоростям будет выглядеть

Для определения постоянной, фигурирующей во всех соотношениях, как константа, используем ранее полученное соотношение для давления газа на стенку. Для этого запишем

Вспомним зависимость давления

Давление выражается через число ударов молекул о стенку в виде

p = 2mv_xdν

при этом число ударов

dν =v_x dn_v

dn_v –число молекул в единице объема с заданной по величине и направлению скоростью

число ударов молекул можно получить из выражения

dν = n

поскольку для давления на стенку требуется задание лишь одной из составляющих по оси х, а значения других составляющих могут быть любыми, то число ударов молекул о стенку получается путем интегрирования по всем значениям составляющих по осям у и z

dν = n

произведение двух интегралов Пуассона учитываем и получаем

dν = n

для давления в этом случае получим

p = 2mn

для вычисления интеграла учтем

- половина интеграла Пуассона.

=(1/2)

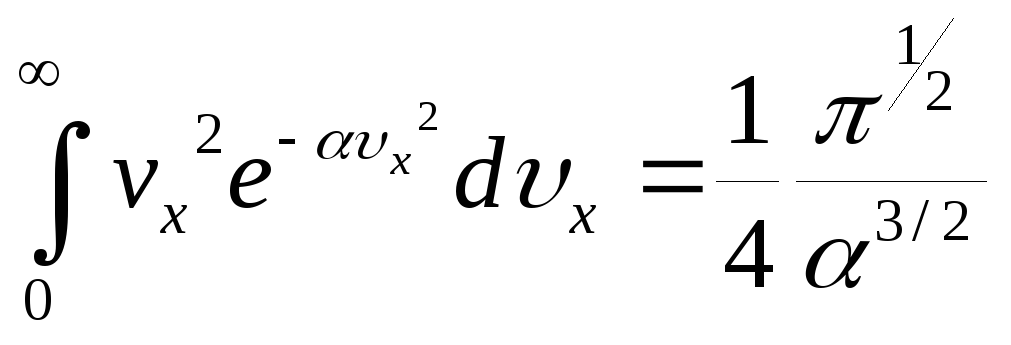
p = mn/(2α)

p= nkT

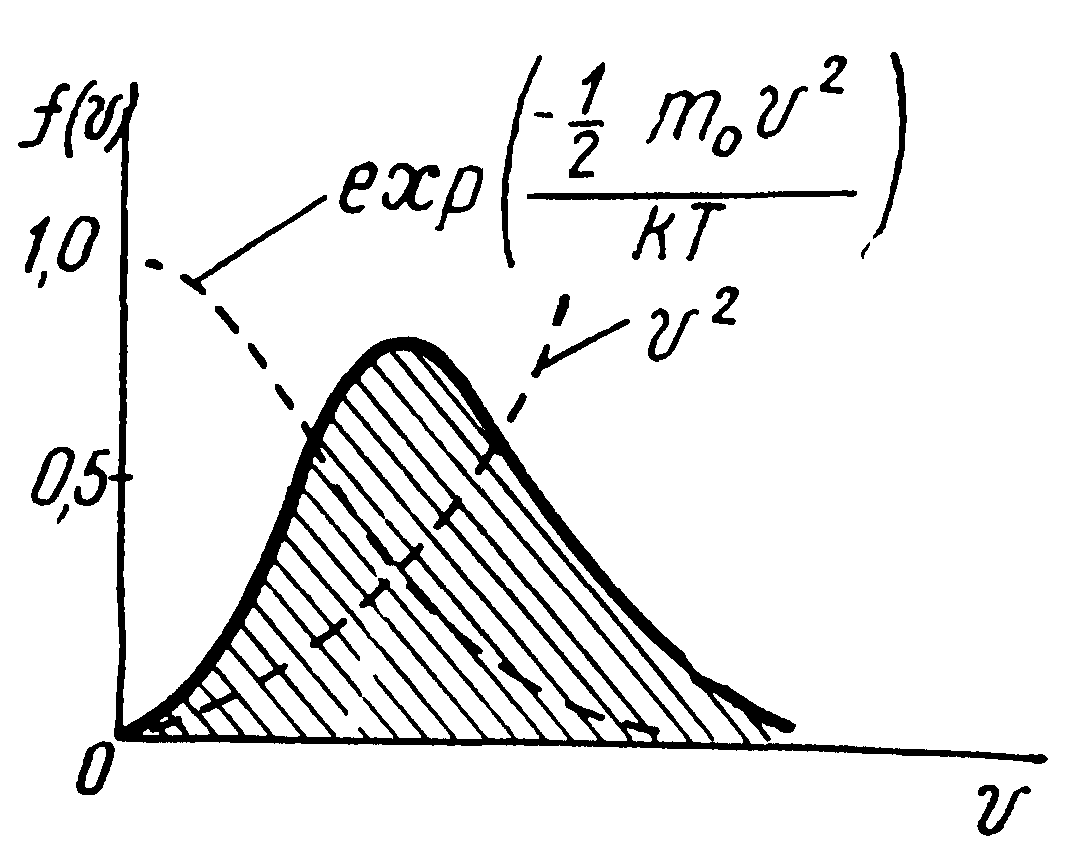
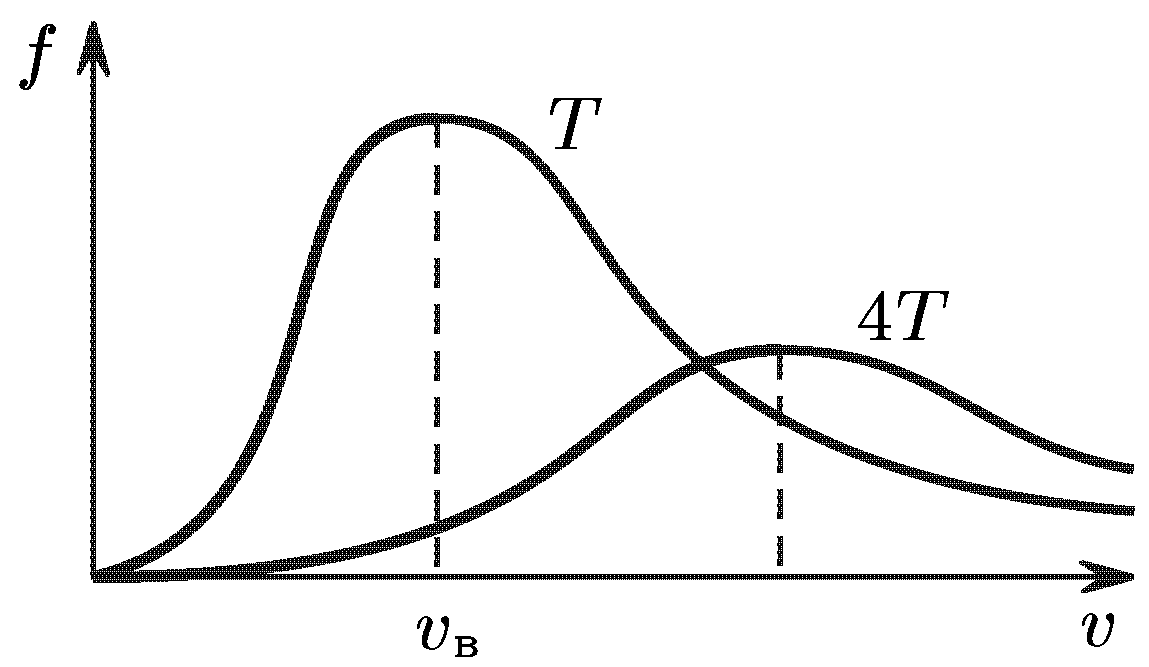
= 4 - распределение Максвелла,

где

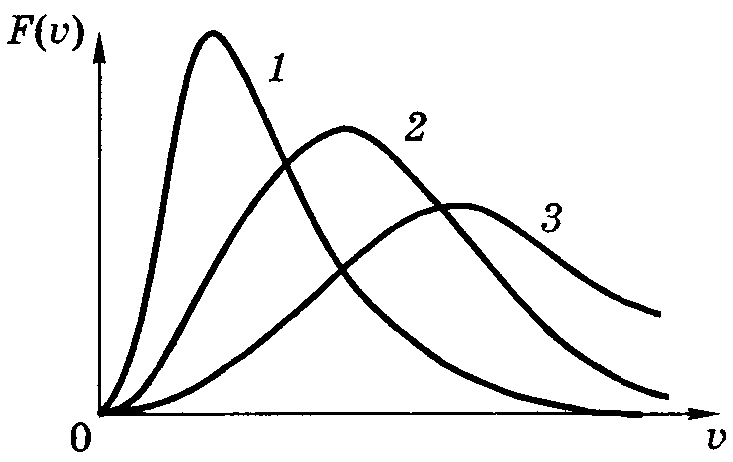
- наивероятнейшая скорость.

- найдем экстремумы.

Найдем среднюю скорость:

Интеграл вычисляется путем интегрирования по частям

Однако, следует учесть, что

Можно дифференцировать этот интеграл по параметру α и умножить результат на -1

Среднеквадратичная скорость представляет собой корень квадратный из среднего значения квадрата скорости

Чтобы это получить, необходимо дважды продифференцировать по параметру половину интеграла Пуассона

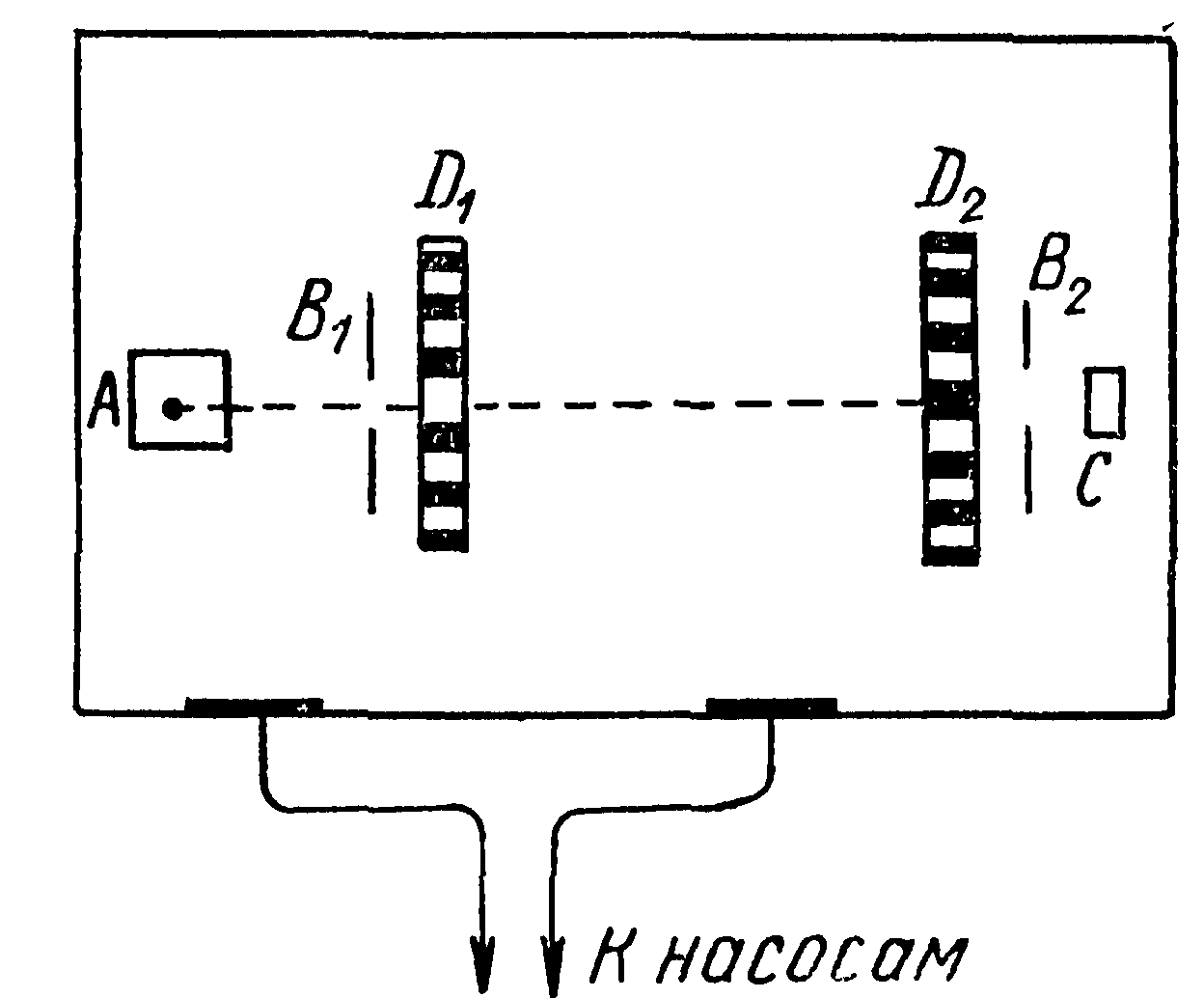
Явление переноса

(неравновесные системы).

Средняя длина свободного пробега молекулы

;

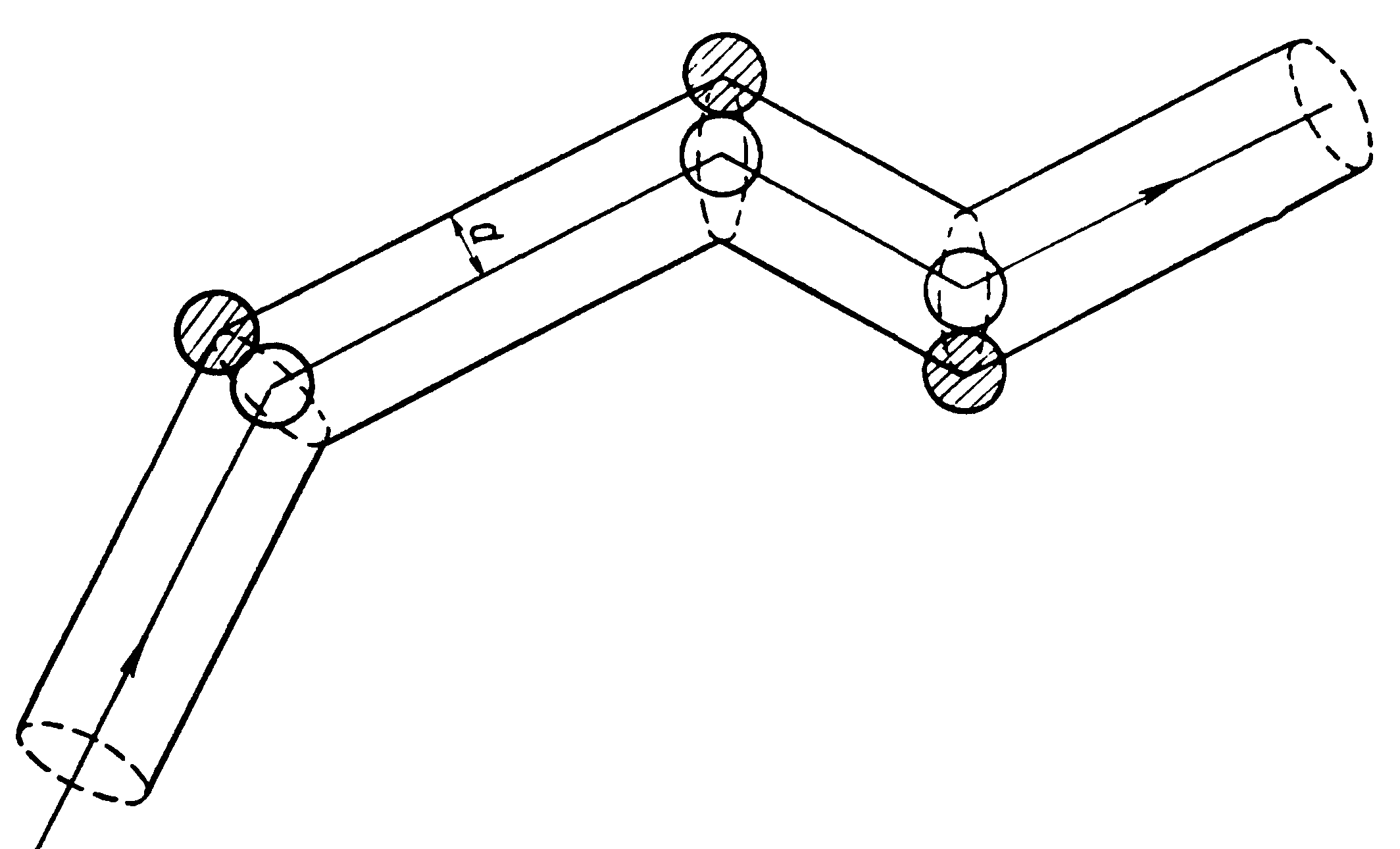
Поскольку средние скорости молекул равны нулю(прямые и противоположные направления движения равноправны)

Произведение скоростей равно нулю.

В этом случае квадрат относительной скорости равен сумме квадратов одинаковых скоростей молекул, а корень квадратный из квадрата относительной скорости равен

;

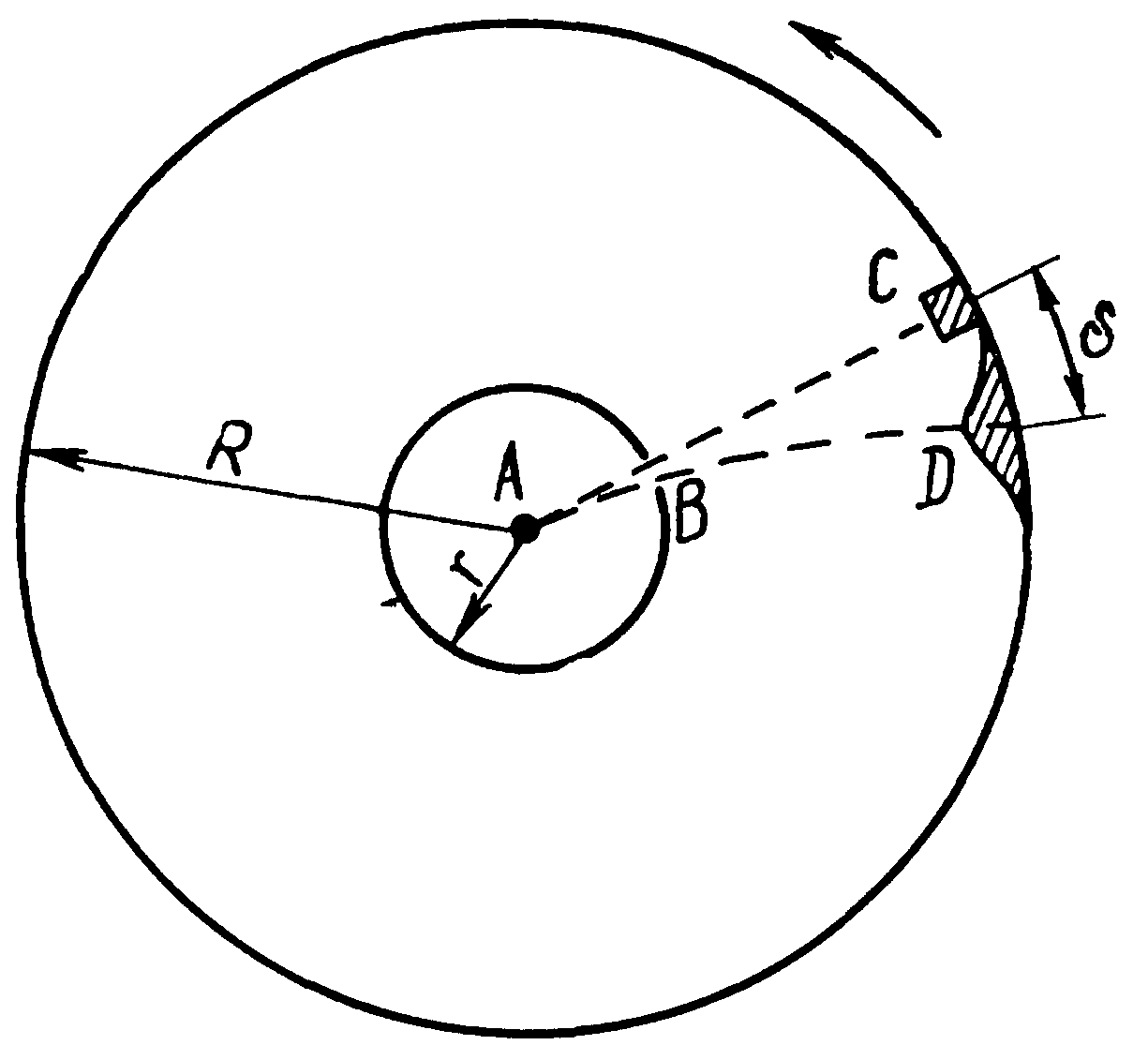
Молекулы совершают хаотические движения, непрерывно сталкиваясь с другими молекулами, находящимися в сечении, площадь которого можно записать в виде:

- сечение, в которое будут попадать молекулы, столкнувшиеся с рассматриваемой.

Путь, пройденный молекулой между столкновениями можно выразить через время между столкновениями

;

Молекула столкнется со всеми молекулами, которые находятся в цилиндре объемом ;

Количество молекул в объеме ;- это число столкновений за время ∆t

Время между столкновениями – это время за которое произошли столкновения на число столкновений за это время

;

Площадь поперечного сечения столкновения

;

Число столкновений в единицу времени

;

Длина свободного пробега молекул

- длина пробега.