Потенциал поля
Пусть в точках М
области пространства V
задано скалярное поле V=V(M). Обозначим
через
-
оператор, соответствующий градиенту
поля V.
; (1)
Скалярное поле V
будет порождать векторное поле
(потенциальное).
Скалярная функция V
будет называться потенциальным
полем
.
;
;
.
То есть потенциалом
поля V
является функция, частные производные,
которые по направлению координат Х,Y,Z
равны проекции силы
на эти оси координат.
Потенциал силы
притяжения:
Производные гравитационного поля: в гравиразведке используют не только первые, но и высшие производные.
;
;
; 
=Vyy;
; 
;
; 
;
Единицы измерения вторых производных: Этвеш 10-9с-2 [Е]
Vz=мГал.
по x,
y,
z;
.
;
; 
;
;
- вертикальный
градиент;
;
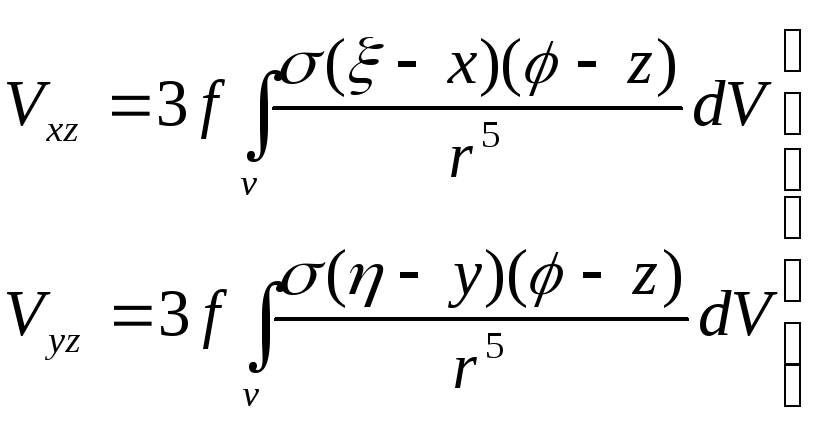- горизонтальные
градиенты силы тяжести;
;
Vxx, Vyy, Vxy – определяют разность кривизны главных нормальный сечений уровенной поверхности и их азимуты.
По физическому смыслу вторые производные делятся на grad силы тяжести Fтяж и кривизны.
Градиент – величина, характеризующая скорость изменения какой-либо величины в пространстве.
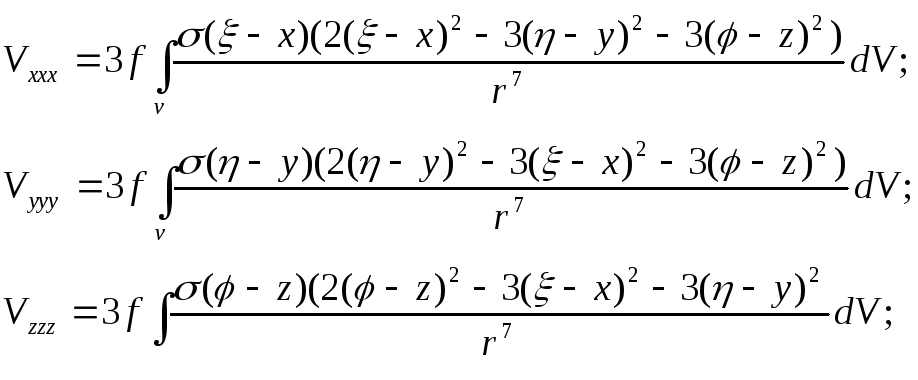
Вторые производные
измеряют гравитационным вариометром
(измеряет все вторые производные) и
градиентометром (
и
).
- полный горизонтальный
градиент grad
(указывает
направление наибольшего изменения силы
тяжести).
и Vxy
определяют
форму уровенной поверхности в точке
наблюдения.
- мера уклонения
уровенной поверхности в данной точке
от сферической.
Для вторых производных потенциала притяжения характерно уравнение Лапласа:
(1)
Потенциал притяжения – функция гармоническая при условии задания: вне притягивающих масс.
В области притягивающих масс сама потенциальная функция и ее производные теряют свою непрерывность, т.е. не являются гармоничными. Эти точки называют особыми.
Уравнение
Пуассона:
(2)
– связывает вторые производные потенциала
притяжения для точек, расположенных
внутри притягивающих масс.
Точечная масса
За точечные массы можно принять только однородные или однородно-слоистые среды конечных размеров. Во всех других случаях размеры масс должны быть бесконечно малы по сравнению с расстоянием между их центрами.
Земной сфероид за точечную массу принять нельзя. Для вычисления силы притяжения земным сфероидом его необходимо разбить на массы бесконечно малых объемов (точечные массы). Притяжение всем земным сфероидам равно интегральной сумме притяжений, создаваемых каждой из помещенных внутри него точечных масс. Суммировать арифметически нельзя, так как направление действия элементов сил притяжения разными точечными массами оказывается различными. Такое суммирование можно выполнить только раздельно для составляющих силы притяжения по осям x, y, z.
Объемная гравитационная и точечная масса
Считаем, что массы,
заключенные в некоторых областях
пространства в объеме V,
распределены
в этом пространстве непрерывно с
некоторой объемной плотностью
:
,
где
и
- элементарные объем и масса, взятые в
некоторой точке
.
- является функцией
точки M.
Внутри поверхности
S,
ограничивающей объем V,
функция является непрерывной и
ограниченной. Вне поверхности S
эта функция равна нулю, т.е. при переходе
из внутренней области во внешнюю значение
меняется скачкообразно.
Общая масса:
,
,
.
Размерами тела можно пренебречь, когда расстояние между наиболее удаленными двумя точками тела намного меньше, чем расстояние между точками M и P, в которых рассматривается притяжение тела, тогда массу тела можно принять за точечную и помещенную в точку.
Масса единицы поверхности (поверхностная плотность) – масса, заключенная между двумя бесконечно близкими поверхностями:
, 
,
[кг∙м-2]
Масса единицы длины (линейная плотность) – тело произвольного сечения, малой пощади, единичной длины.
,
;
Для цилиндра:
