6. Последовательность выполнения расчетного задания

Подводя итоги, сформулируем последовательность действий при выполнении расчетного задания.

6.1. Профилирование сопла

• Находим критическую скорость по формуле (12), безразмерную критическую плотность по таблицам газодинамических функций, либо по соотношению (10), размерное значение плотности в критическом сечении – также из равенства (10), предварительно найдя плотность заторможенного газа во входном сечении сопла по уравнению состояния (21).

• Рассчитываем площадь критического сечения , подставив данные в формулу (20), и диаметр критического сечения из равенства (22).

• По известным давлению торможения входного сечения 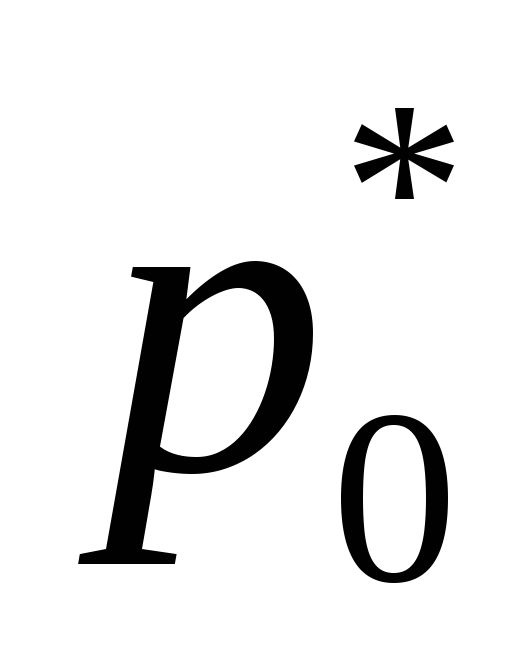и противодавлению расчетного режима определяем ; в таблицах газодинамических функций находим соответствующие этому безразмерному давлению функцию тока 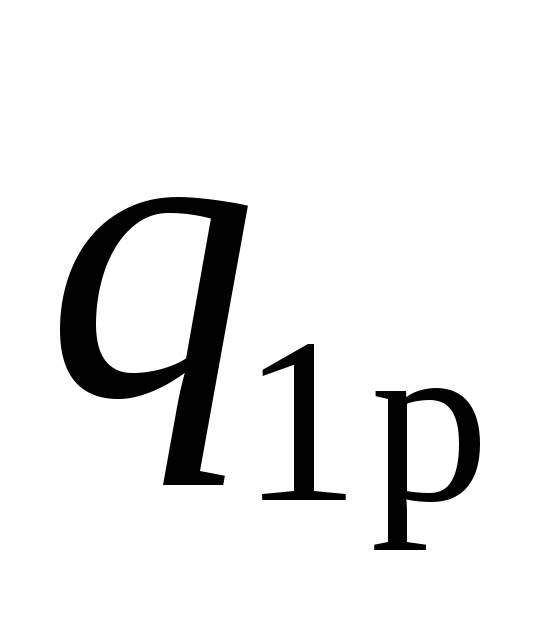и остальные параметры с индексом «1р».

• Определяем площадь выходного сечения согласно (23) и диаметр выходного сечения.

• По двум диаметрам ( и ) и углу раствора конуса строим расширяющуюся часть сопла.

• Пристраиваем к расширяющейся конусообразной части сопла суживающуюся дозвуковую часть, взяв в качестве образующих произвольные кривые (они должны располагаться симметрично относительно оси сопла и для протекающего между ними потока газа быть выпуклыми, так чтобы площадь сечения вблизи входа в сопло была весьма велика (в пределе стремилась к бесконечности), что согласуется с условиями, заданными на входе в сопло, поскольку при постоянном массовом расходе согласно уравнению неразрывности в форме (13) нулевой скорости (заторможенный газ) соответствует при конечном значении плотности бесконечно большая площадь входного сечения (см. рис.2).

6.2. Построение расходной характеристики

• В таблицах газодинамических функций находим второе (помимо ) безразмерное давление, для которого функция тока равна . При необходимости применяем линейную интерполяцию для более точного определения искомого давления .

На графике зависимости безразмерного приведенного расхода от безразмерного выходного давления строим ту его часть, которая соответствует режиму запирания: при

• Для построения оставшейся части графика делим интервал 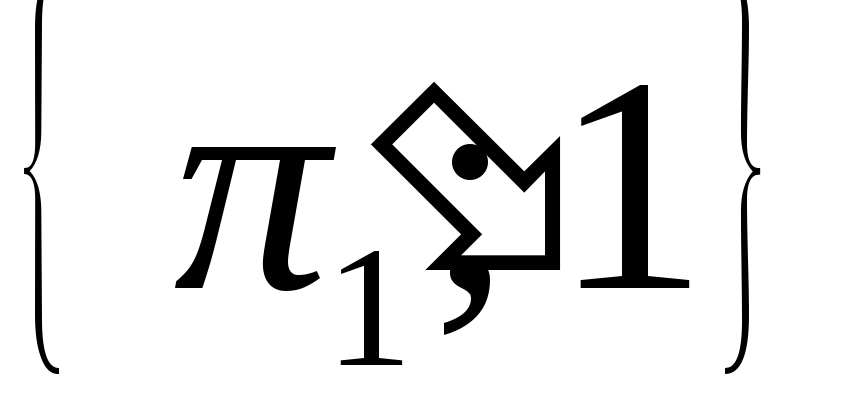на несколько промежутков по давлению (берем 5 – 7 значений безразмерного давления между и 1; удобно брать табличные значения ). По таблицам находим для каждого соответствующую ему функцию тока q, определяем безразмерный приведенный расход и наносим точку на график. Затем все построенные точки соединяем плавной падающей кривой (см. рис.3).

6.3. Расчет параметров до и после скачка уплотнения, а также в выходном сечении

• Задаем положение скачка площадью сечения в соответствии с равенством (28).

• Определяем функцию тока слева от скачка по формулам (30a) или (30b).

• При помощи таблиц находим по функции тока скоростной коэффициент 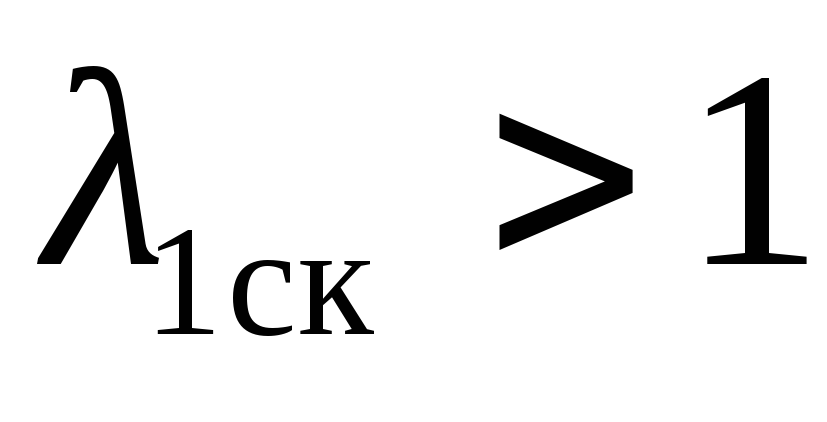и остальные безразмерные параметры с индексом «1ск». При необходимости применяем линейную интерполяцию.

• Определяем безразмерную скорость справа от скачка по формуле Прандтля (31), и по таблицам, также с использованием линейной интерполяции, находим и остальные параметры с индексом «2ск».

• Рассчитываем функцию тока в выходном сечении , пользуясь выражением (32); по таблицам определяем и остальные параметры «1» на выходе из сопла.

• Находим коэффициент неизоэнтропийности 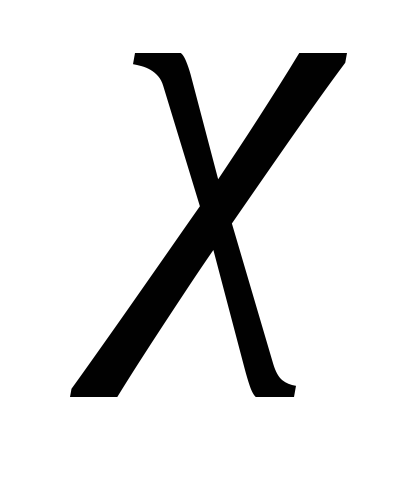по формуле (34), затем безразмерное давление «теоретического» режима по (35). При помощи таблиц определяем скоростной коэффициент и остальные параметры «теоретического» режима.

• Определяем КПД сопла по формуле (36).