7.5. Покроковий контроль точності. Метод Рунге-Кутта-Мерсона
Один зі способів,
який гарантує точність розв’язання
задачі Коші, – розв’язувати задачу з
кроками, рівними
і
,
та порівнювати результати у вузлових
точках, що відповідають більшому кроку.
Будемо вважати, що при використанні
методу Рунге-Кутта
-го
порядку абсолютна покрокова похибка
повинна знаходитись в межах
.
Тоді, згідно принципу
Рунге,
обрахунки здійснюються по системі
вузлів
з кроком
та по системі вузлів
з кроком
.
При парних
друга система буде співпадати з першою,
тобто
.
Перехід від поточної точки
з наближеним значенням розв’язку в ній
до наступної точки
один раз здійснюється за один крок
довжини
і приводить до значення
,
а другий раз – за два кроки довжини
(„транзитом” через точку
зі значенням
)
і дає значення
.
Поправка Річардсона в такому випадку буде складати величину
.
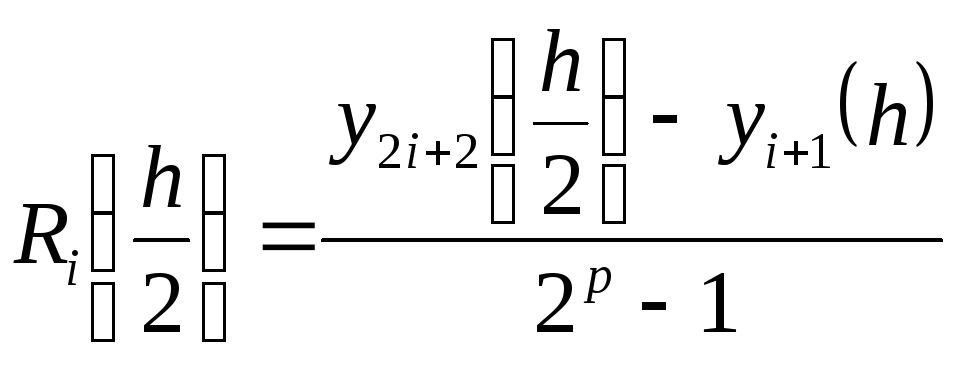Якщо величина
менша заданого
,
то можна вважати, що похибка наближеної
рівності
не перевищує
.
Якщо ж
,
то необхідно зменшити розрахунковий
крок
.
При умові
варто спробувати виконувати обчислення
далі з більш великим кроком (наприклад,
подвоїти
).
Описана технологія покрокового контролю точності чисельного розв’язування задачі Коші та автоматичного вибору розрахункового кроку при цьому в такій безпосередній формі потребує значної кількості обчислень для кроку меншої довжини, які доведеться повторити, якщо буде визначено, що узгодженість недостатньо добра.
Прагнення підвищити обчислювальну ефективність призвело до появи різних версій методів Рунге-Кутта. Одним із таких методів є метод Рунге-Кутта-Мерсона. Даний метод задає процедуру, яка визначає, чи вірна довжина кроку h використовується. На кожному кроці отримуємо два різних наближення та порівнюємо їх. Якщо дві відповіді узгоджуються, то наближення приймається. Якщо обидві відповіді не узгоджуються з заданою точністю, то довжина кроку зменшується. Якщо відповіді узгоджуються з більшою кількістю значущих цифр, ніж необхідно, то довжина кроку збільшується.
На кожному
-му
кроці послідовно обчислюють:
,
,
,
,
,
.
Після цього обраховують величину
і проводять
порівняння. Якщо значення
виявиться більше заданого допустимого
рівня абсолютної похибки
,
то крок зменшують вдвічі і повертаються
на початок обчислень, тобто заново
обчислюють
і т.д. Якщо
,
то вважають
з точністю
.
При переході до наступного кроку
виконується перевірка на можливість
збільшення розрахункового кроку: якщо
,
то далі обрахунки проводяться з кроком
.
7.6. Засоби середовища matlab розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку методами Рунге-Кутта
В MATLAB існує цілий ряд вбудованих функцій, призначених для розв’язання задачі Коші для звичайних диференціальних рівнянь першого порядку. Функції ode23 та ode45 використовують методи Рунге-Кутта другого-третього і четвертого-п’ятого порядку відповідно з автоматичним вибором розміру кроку.
Звернення до функцій ode23 та ode45 здійснюється однаково та виконується наступним чином (синтаксис наведений для версії 7.0):
[x,y] = ode23(odefun,xspan,y0,options,p1,p2,...)
і
[x,y] = ode45(odefun,xspan,y0,options,p1,p2,...)
Обов’язковими вхідними параметрами цих функцій є:
odefun – ім’я функції (у вигляді рядкової змінної), що задає праву частину диференціального рівняння (або системи рівнянь). Рівняння повинні бути записані в нормальній формі y'=odefun(x,y);
xspan=[x0 xfinal] – вектор, що задає інтервал зміни незалежної змінної. x0 – початкова точка, xfinal – останнє значення аргументу, при якому завершуються розрахунки;
y0 – вектор початкових значень залежної змінної.
Вимоги до точності та інші параметри чисельного розв’язання задаються в MATLAB по замовчуванню (точність при цьому складає 10-3). Змінити ці настройки дозволяє додатковий аргумент options, який необхідно формувати за допомогою функції odeset (див. help odeset).
Додаткові параметри p1,p2,… у функцій ode23 та ode45 вказують, якщо їх необхідно передати в функцію odefun(x,y,p1,p2,…), а також в інші функції, задані в options.
Вихідні параметри функцій ode23 та ode45:
x – вектор, що містить вузлові значення аргументу, в яких було знайдено розв’язок;
y – масив, який містить розв’язок задачі Коші у відповідних вузлових значеннях незалежної змінної x.
Приклад 7.5. За допомогою вбудованої функції MATLAB ode45 знайдемо розв’язок задачі Коші з прикладу 7.3:
,
,
.
Спочатку створимо файл-функцію, в якій визначимо праву частину диференціального рівняння:
function z=f(x,y)
z=(x-y)/2;
Звернемось до функції ode45, задавши першим вхідним аргументом ім’я цієї створеної функції:
>> ode45('f',[0,3],1)
В результаті виконання даної команди на екрані з’явиться графік розв’язку задачі Коші (рис. 7.4).
Рис. 7.4. Графічне представлення розв’язку задачі Коші, отримане за допомогою функції ode45