7.4. Метод Рунге-Кутта та його модифікації розв’язування задачі Коші для звичайного диференціального рівняння першого порядку

Метод Ейлера та його модифікації відносяться до сімейства методів Рунге-Кутта. Ці методи виводяться з відповідних методів степеневих рядів (Тейлора) таким чином, щоб остаточна загальна помилка методів не перевищувала порядку . Методи були розроблені для того, щоб на кожному кроці виключити необхідність підрахунку похідних вищих порядків. Методи Рунге-Кутта будуються для будь-яких порядків N, що обумовлено точністю.

Ма́ртин Вільге́льм Кутта́ (Martin Wilhelm Kutta) (1867-1944) – німецький математик і фізик. Навчався в Бреславському університеті (зараз Вроцлавський) з 1885 по 1890 рр., продовжив навчання в Мюнхені до 1894 р., де став асистентом В. Діка. З 1898 р. проводить рік в університеті Кембриджа. Викладав у Вищій технічній школі в Штутгарті, де став у 1911 р. професором. В 1901 р. спільно з К. Рунге розробив метод чисельного розв’язування задачі Коші для звичайних диференціальних рівнянь та їх систем (метод Рунге-Кутта).

Для побудови даних методів можна використовувати наступний загальний підхід. В процесі обчислень фіксуються деякі числа

.

Послідовно обчислюємо

(7.20)

та покладаємо

.

(7.21)

Розглянемо питання про вибір параметрів . Позначимо . Якщо – достатньо гладка функція своїх аргументів, то і – гладкі функції параметру h. Припустимо, що настільки гладка, що існують похідні , а вибрані таким чином, що . Крім того, припустимо, що існує деяка гладка функція , для якої відповідне значення

.

(7.22)

Згідно формули Тейлора виконується рівність

,

(7.23)

де . Величина називається похибкою методу на кроці, а s – порядком похибки методу.

Таким чином, формули (7.20)-(7.22) виражають метод Рунге-Кутта s-го порядку розв’язування задачі Коші (7.2)-(7.3).

Розглянемо частинні випадки методу Рунге-Кутта.

1. При маємо:

,

,

.

Рівність виконується для всіх гладких функцій лише у випадку . При даному значенні з формули (7.21) отримується формула методу Ейлера.

2. Розглянемо випадок . Тоді

де .

Відповідно до початкового диференціального рівняння

,

.

Обчислюючи похідні функції та підставляючи у вирази для значення , отримаємо

, ,

.

Співвідношення буде виконуватись для всіх лише в тому випадку, коли одночасно виконуються наступні три рівності відносно чотирьох параметрів:

, , .

(7.24)

Довільно задаючи значення одного з параметрів та визначаючи значення інших з системи (7.24), отримаємо різні методи Рунге-Кутта з порядком похибки :

1) при з (7.24) отримаємо: , що відповідає парі розрахункових формул (7.15) методу Ейлера-Коші.

2) при отримаємо: , що відповідає розрахунковим формулам удосконаленого методу Ейлера.

З (7.23) випливає, що головна частина похибки на кроці становить , тобто ця похибка пропорційна третій степені кроку.

3. У випадку аналогічно можна вивести метод Рунге-Кутта третього порядку. Найбільш застосовна сукупність розрахункових формул при :

,

, .

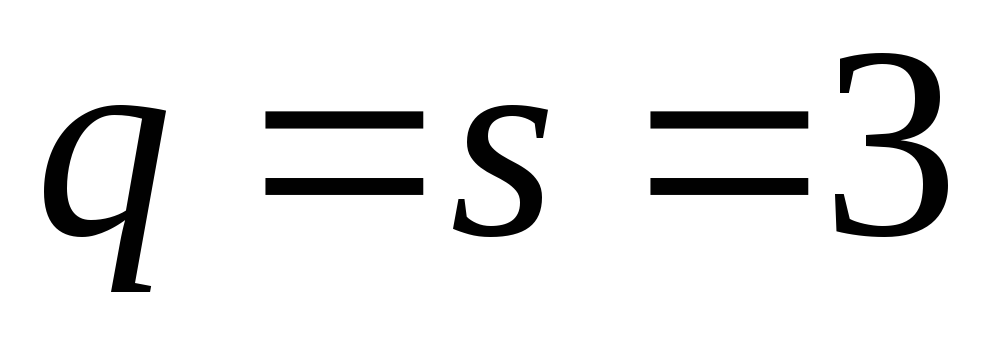4. На практиці найчастіше застосовується метод Рунге-Кутта четвертого порядку, формули якого отримують при . Він базується на обчисленні значення по попередньому за формулою:

, ,

(7.25)

де мають вигляд

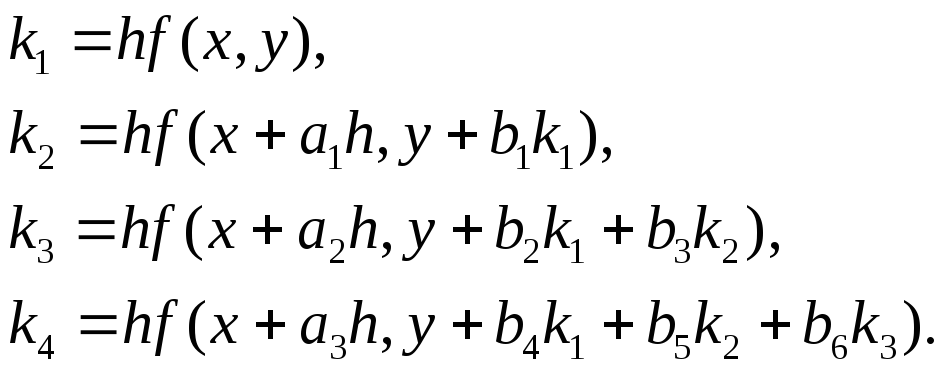
Тут коефіцієнти , такі, що локальна похибка на кроці має порядок . Рунге і Кутт отримали наступну систему рівнянь для визначення , , :

.

Отримані 11 рівнянь вміщують 13 змінних, тому для їх розв’язання потрібні 2 додаткові умови. Найчастіше всього використовують наступні умови:

та .

(7.26)

За таких умов розв’язком системи рівнянь буде:

.

(7.27)

Підставляючи значення (7.26) і (7.27) в рівняння (7.25), отримаємо формулу для стандартного методу Рунге-Кутта 4-го порядку:

, ,

(7.28)

де

, .

(7.29)

Геометричний зміст використання методу Рунге-Кутта четвертого порядку з розрахунковими формулами (7.28)-(7.29) полягає в наступному (рис. 7.3).

Рис. 7.3. Геометрична інтерпретація одного кроку

методу Рунге-Кутта четвертого порядку

З точки (точка А на рис. 7.3) зміщуються в напрямку, що визначається кутом , для якого . На цьому напрямку обирається точка М з координатами . Потім з точки зміщуються в напрямку, який визначається кутом , для якого , і на цьому напрямку обирається точка N з координатами . Нарешті, з точки зміщуються в напрямку, що визначається кутом , для якого , і на цьому напрямку обирається точка Е з координатами . Цим задається ще один напрямок, який визначається кутом , для якого (відрізок AG). Чотири отриманих напрямки усереднюються у відповідності з (7.28)-(7.29). На цьому остаточному напрямку обирається точка H з координатами , яка є стартовою для -го кроку методу. На рис. 7.3 відрізок ВН – підсумкова крокова поправка , яка є продуктом усереднення з вказаними коефіцієнтами чотирьох довжин відрізків BC, BD, BE, BG.

Приклад 7.4. Розв’яжемо методом Рунге-Кутта четвертого порядку задачу Коші з прикладу 7.3:

, на проміжку .

Наведемо зразок підрахунку коефіцієнтів для кроку :

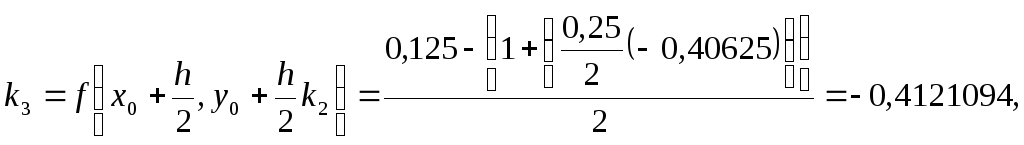
Всі інші значення розраховуються аналогічно.

Накопичена похибка в методі Рунге-Кутта складається з елементарних похибок, які виникають на кожному кроці обчислень. Якщо на кожному кроці похибка пропорційна п’ятій степені кроку, тобто має порядок , то після N кроків накопичена похибка для методу Рунге-Кутта четвертого порядку буде становити .

Отже, для маємо методи Рунге-Кутта q-го порядку. Їх використання пов’язане з обчисленням правої частини у q точках. При отримують метод Рунге-Кутта четвертого порядку. Тому в цьому випадку розрахункові формули не мають практичного застосування. Метод Рунге-Кутта п’ятого порядку одержують при , а шостого – при . Очевидно, що зі збільшенням q обсяг обчислень у методі Рунге-Кутта зростає. Тому до методу Рунге-Кутта вищих порядків (понад 4) вдаються переважно тоді, коли обчислення проводяться з великим кроком. Найпопулярнішим є метод Рунге-Кутта четвертого порядку. Найбільш авторитетні спеціалісти стверджують, що немає необхідності використовувати метод вищого порядку, оскільки збільшення точності не компенсує додаткову складність обчислень. Якщо необхідна більш висока точність, то можна використовувати менший крок або модифікований метод.

Перевага методів Рунге-Кутта полягає в тому, що алгоритми, які одержують на їхній основі, є однорідними, тобто не змінюються з переходом від однієї точки до іншої. Крім цього, в методах Рунге-Кутта можна змінювати крок інтегрування відповідно до потреби точності обчислень без значного ускладнення алгоритму. Основним недоліком цих методів є те, що для обчислення наближеного значення розв’язку в окремій точці, необхідно обчислювати значення функції у декількох точках.

Програмна реалізація методу Рунге-Кутта четвертого порядку на мові середовища MATLAB наведена в лістингу 7.1.

Лістинг 7.1.

function [x,y]=runge4(y0,a,b,n)

% runge4 – метод Рунге-Кутта четвертого порядку

% Права частина диференціального рівняння повинна бути

% задана у функції f(x)

% >> [x,y]=runge4(y0,a,b,n)

% Вхідні аргументи:

% y0 – початкове значення;

% a, b – межі інтервалу;

% n – кількість підінтервалів

% Вихідні аргументи:

% x – вектор вузлів, в яких знайдений розв’язок;

% y – вектор зі значеннями функції-розв’язку у вузлах х

if a>=b

error('Неправильні межі (a<b)');

end

h=(b-a)/n;

x(1)=a;

y(1)=y0;

for i=1:n

k1=f(x(i),y(i));

k2=f(x(i)+h/2,y(i)+h/2*k1);

k3=f(x(i)+h/2,y(i)+h/2*k2);

k4=f(x(i)+h,y(i)+h*k3);

y(i+1)=y(i)+h/6*(k1+2*k2+2*k3+k4);

x(i+1)=x(i)+h;

end