7.3.2. Виправлений метод Ейлера

Нехай знайдено наближене значення розв’язку задачі (7.2)-(7.3), і необхідно обчислити , де . Запишемо розклад розв’язку за формулою Тейлора -го порядку, приймаючи за базову точку (тобто за степенями ), і покладемо в цьому розкладі . Маємо

.

(7.9)

Якщо обмежитись двома доданками в правій частині розкладу (7.9), то отримаємо звичайний метод Ейлера (7.5). Подивимось, що дає врахування третього доданку.

При із (7.9) слідує рівність

.

(7.10)

Значення першої похідної в точці , в силу зв’язності (7.2), приблизно відоме:

.

(7.11)

Диференціюючи (7.2) за формулою повної похідної

знаходимо наближене значення другої похідної:

.

(7.12)

Підставляючи наближені вирази для , та в рівність (7.10), отримуємо наступну формулу для обчислення при :

.

(7.13)

Метод, який визначається даною формулою будемо називати виправленим методом Ейлера.

Так як при формули (7.11) і (7.12) є точними, а , згідно початкової умови (7.3), то на першому кроці обчислень за формулою (7.13) буде виникати похибка, пов’язана тільки з усіканням ряду Тейлора. Звідси слідує, що локальна похибка методу (7.13) складає величину , а це означає, що виправлений метод Ейлера відноситься до методів другого порядку.

7.3.3. Удосконалений метод Ейлера (метод середньої точки)

За цим методом розв’язок задачі Коші (7.2)-(7.3) обчислюється за формулами

, .	(7.14)

7.3.4. Метод Ейлера-Коші (метод Хойна)

Даний метод являє собою один із варіантів спільного використання методу Ейлера та неявного методу трапецій. В методі Ейлера-Коші використовують наступний порядок обчислень:

, , .

(7.15)

Геометрично це означає, що визначається напрямок інтегральної кривої в точці та в допоміжній точці , а в якості остаточного береться середнє значення цих напрямків.

7.3.5. Удосконалений метод Ейлера-Коші з ітераційною обробкою

Зрозуміло, що можна досягти більшої точності, якщо, виходячи з того ж самого початкового наближення

,

(7.16)

зробити не одну, а кілька ітерацій за методом трапецій:

.

(7.17)

Ознакою закінчення ітераційного процесу є умова:

.

7.3.6. Уточнений метод Ейлера

Щоб отримати наступну модифікацію методу Ейлера, проінтегруємо рівняння (7.2) на відрізку :

,

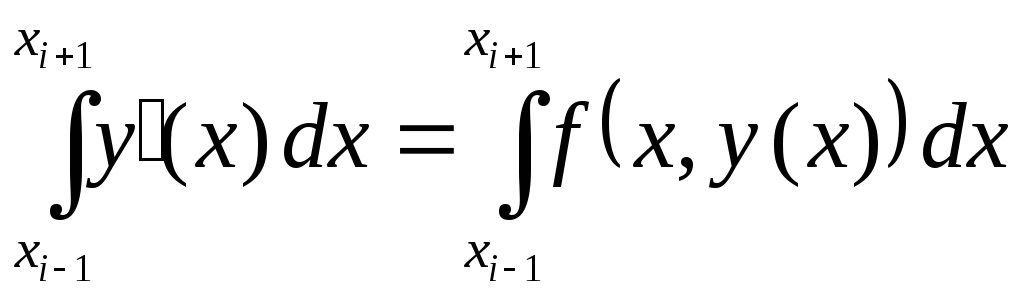звідки слідує рівність

.

(7.18)

Застосовуючи до останнього інтегралу одноточкову квадратурну формулу середніх прямокутників і замінюючи значення і відомими наближеними значеннями та відповідно, із (7.18) виводимо формулу для обчислення наближеного значення :

,

(7.19)

яку ми будемо називати уточненим методом Ейлера.

Звернемо увагу на одну принципову відмінність методу (7.19) від усіх інших розглянутих до цього моменту методів: метод (7.19) є двохкроковим. Тут для обчислення значення використовуються два попередніх значення та . Двохкроковість накладає певні обмеження, принаймні, на початок чисельного процесу: значення не може бути знайдене безпосередньо за цим методом. Тому недостатню для процесу (7.19) другу початкову точку треба обчислювати іншим методом, наприклад, методом Ейлера. Так, необхідне значення можна знайти за формулами (7.14), а потім продовжувати обрахунки за формулою (7.19).