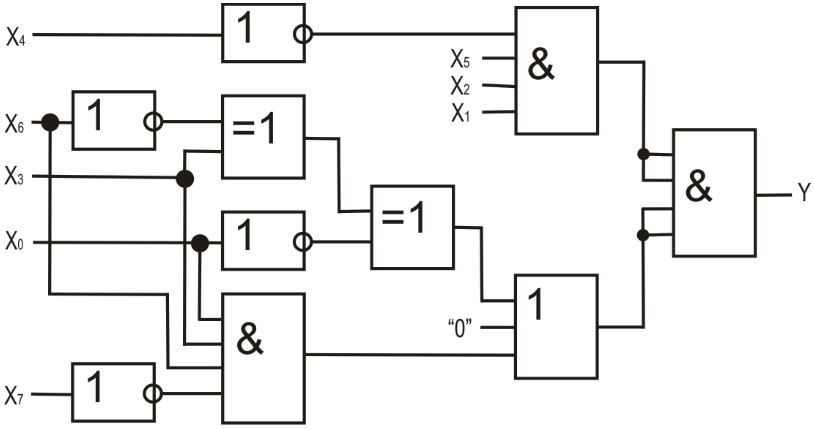
- •Лабораторна робота 2
- •Теоретичні відомості
- •Побудова схем електричних функціональних для відображення логічних перетворень сигналів.
- •Побудова схем електричних функціональних з блочним групуванням логічних елементів.
- •Реалізація схем електричних функціональних на наявній елементній базі (в заданому базисі)
- •Завдання лабораторної роботи 2
Реалізація схем електричних функціональних на наявній елементній базі (в заданому базисі)
Схема електрична функціональна може використовуватись не лише як засіб ілюстрації принципів функціонування певних об’єктів, але і як певний етап в розробці проектованого об’єкта.
Так, наприклад, схема електрична функціональна може бути основою для розробки схеми електричної принципової проектованого об’єкта або для його реалізації на програмованих інтегральних схемах (програмованих логічних матрицях та інше).
В інтегральному виконанні (у вигляді стандартних або програмованих мікросхем) випускаються далеко не всі елементи, використовувані нами на загальних схемах електричних функціональних. В таких випадках виникає потреба побудови схем електричних функціональних на існуючій або на наявній елементній базі.
Примітка: Досить часто задача побудови схем електричних функціональних на наявній елементній базі зводиться до побудови схем в заданому базисі, тобто, передбачає перетворення функцій під заданий базис. Методи перетворення функцій визначаються законами алгебри логіки і не відносяться до задач нашого курсу, тому зупинятися на вирішенні подібних завдань не будемо.
Фактично, задача побудови схеми для реалізації заданої функції на наявній елементній базі зводиться до розв’язку сукупності задач побудови на наявній елементній базі схем для реалізації часткових функцій, з яких складається задана.
Розглянемо приклад реалізації функції 2.1 на наявній елементній базі за умови, що для побудови схеми можуть використовуватись в необмеженій кількості наступні логічні елементи: “НЕ”, “2АБО-НЕ”, “4І”, “3АБО”, “2 виключальне АБО”.
Виконаємо перетворення часткових функцій (функції 2.2-2.5), з яких складається функція 2.1, для забезпечення можливості їх реалізації в заданому базисі.
Проаналізуємо
функцію
![]() (функція
2.2).
В ході аналізу можна дійти висновку, що
зазначену функцію можна реалізувати
на
наявній елементній базі з
використанням елементів “НЕ”
і “2 виключальне АБО”.
(функція
2.2).
В ході аналізу можна дійти висновку, що
зазначену функцію можна реалізувати
на
наявній елементній базі з
використанням елементів “НЕ”
і “2 виключальне АБО”.
Пояснимо методику реалізації функції 2.2 вже відомим нам методом її розбиття на часткові функції, але з урахуванням особливостей обраної елементної бази.
Спочатку виділяємо в функції 2.2 функції інвертування вхідних сигналів, які реалізовуються елементом “НЕ” і є необхідними для подальшого розрахунку значення функції 2.2:
![]() ,
,
![]() . (2.6)
. (2.6)
На підставі часткових функцій 2.6 функцію 2.2 можна записати у вигляді:
![]() (2.7)
(2.7)
В функції 2.7 послідовно виділяємо дві часткові функції, які можуть реалізовуватись елементами “2 виключальне АБО”:
![]() ,
,
![]() . (2.8)
. (2.8)
Функцію 2.2 з функції f1.4 можна отримати інвертуванням, яке реалізується елементом “НЕ”:
![]() (2.9)
(2.9)
Таким чином, нами відслідковані всі перетворення (обчислення часткових функцій), необхідні для реалізації функції 2.2 з використанням елементів “НЕ” (3 шт. – функції f1.1, f1.2 і f1.5) і “2 виключальне АБО” (2 шт. – функції f1.3 і f1.4).
Шляхом зворотніх перетворень, на підставі функцій 2.6-2.9 функцію 2.2 можна записати з розбиттям на фрагменти, орієнтовані на реалізацію в заданому базисі:
![]()
Проаналізуємо
функцію
![]() (функція
2.3).
Дану функцію можна реалізувати на
наявній елементній базі з
використанням елементів “НЕ”
і “4І”:
(функція
2.3).
Дану функцію можна реалізувати на
наявній елементній базі з
використанням елементів “НЕ”
і “4І”:
![]() ,
,
![]() . (2.10)
. (2.10)
Функцію
![]() (функція
2.4)
розглядаємо в скороченому вигляді
(функція
2.4)
розглядаємо в скороченому вигляді
![]() ,
з урахуванням наявності розглянутих
рішень для часткових її функцій f1
і f2.
Дану функцію можна реалізувати на
наявній елементній базі двома способами
з
використанням елементів “2АБО-НЕ”
і
“НЕ”
або з
використанням елемента “3АБО”.
,
з урахуванням наявності розглянутих
рішень для часткових її функцій f1
і f2.
Дану функцію можна реалізувати на
наявній елементній базі двома способами
з
використанням елементів “2АБО-НЕ”
і
“НЕ”
або з
використанням елемента “3АБО”.
З використанням елемента “2АБО-НЕ” можна виконати логічне додавання двох аргументів, але результат буде про інвертованим, тобто отримане рішення буде частковою реалізацією функції f3:
![]() .
(2.11)
.
(2.11)
Функцію
f3
з
функції 2.11 можна
обчислити повторним інвертуванням
отриманого результату останньої (як
відомо, за законами алгебри логіки
![]() ):
):
![]() .
(2.12)
.
(2.12)
Елемент “3АБО” реалізує логічне додавання трьох аргументів, тому для реалізації функції f3 з використанням цього елемента її початково треба перетворити в функцію від трьох аргументів таким чином, щоб результуюче значення функції не змінилося. За законами алгебри логіки отримуємо три варіанти функції f3 з трьома аргументами:
![]() .
(2.13)
.
(2.13)
![]() . (2.14)
. (2.14) ![]() .
(2.15)
.
(2.15)
Зупинимось на варіанті 2.15.
Функцію
![]() реалізовуємо із застосуванням елемента
“НЕ”
і двох елементів “4І”:
реалізовуємо із застосуванням елемента
“НЕ”
і двох елементів “4І”:
![]() ,
,
![]() ,
, ![]() .
.