2. Декартовы координаты на плоскости и в пространстве.

2.1 Декартовы координаты на плоскости.

Декартова прямоугольная система координат на плоскости задается следующим образом. Выберем точку О – начало координат. Проведем через точку О две взаимно ортогональные (перпендикулярные) прямые, на каждой из которых выберем положительное направление и масштаб (единичный отрезок), превращающие прямые в числовые оси (см. рис. 2.1). Одну из осей назовем осью абсцисс (осью Оx), другую – осью ординат (осью Оy). Кратчайший поворот на 90⁰ от оси Ох к оси Оy совершается против часовой стрелки.

Систему координат обозначим Оху, а плоскость с введенной на ней декартовой прямоугольной системой координат назовем координатной плоскостью. Каждая точка M координатной плоскости Оху однозначно определяется числами х и у – ортогональными проекциями точки М на оси координат Ох и Оу, называемыми координатами точки; пишем М(х;у), читаем "точка М с координатами х и у", х – абсцисса точки М, у – ордината точки М.

2.2 Основные задачи аналитической геометрии на плоскости.

2.2.1. Расстояние между двумя точками.

Н

у

айдем расстояние d между точками и координатной плоскости

О ху (рис. 2.2 а). Это расстояние равно длине отрезка , который является гипотенузой прямоугольного треугольника , и по теореме Пифагора

(2.1)

2.2.2. Деление отрезка в данном отношении.

Рассмотрим на координатной плоскости Оху отрезок с концами в точках и (см. рис. 2.2 б).

Говорим, что точка М делит отрезок в отношении , считая от точки , если . Найдем координаты точки , делящей отрезок в данном отношении , т. е. . Из рис. 2.2 б ясно, что

или .

Заметим, что левая часть последнего равенства положительна при любом следовании точек и на прямой, проходящей через точки и .

Из последнего равенства получаем

, .

Аналогично получаем .

Итак, мы нашли координаты точки , делящей отрезок в отношении :

. (2.2)

Из формул (2.2) при получим координаты середины отрезка :

(2.3)

2.2.3. Площадь треугольника.

Рассмотрим на плоскости Оху треугольник с вершинами в точках и . Тогда площадь треугольника вычисляется по формуле

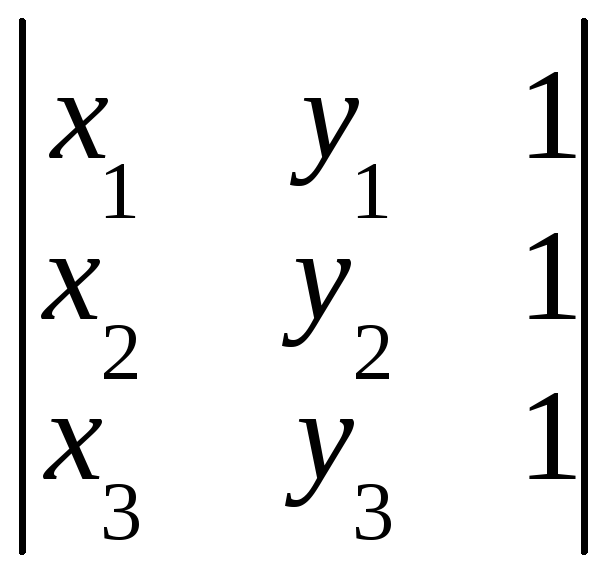. (2.4)

2.3. Декартовы координаты в пространстве.

Декартова прямоугольная система координат в пространстве задается следующим образом. Выберем точку О – начало координат. Проведем через точку О три взаимно ортогональные прямые, на каждой из которых выберем положительное направление и масштаб (превращающие эти прямые в числовые оси). Эти оси координат называются соответственно осью абсцисс (осью Ох), осью ординат (осью Оу) и осью аппликат (осью Оz). Оси ориентированы таким образом, что, если смотреть от положительного направления оси Оz, то кратчайший поворот от оси Ох к оси Оу виден совершающимся против часовой стрелки (см. рис. 2.3).Систему координат обозначим Охyz, а пространство соответственно координатным пространством. Тогда для каждой точки М пространства определены координаты х,у и z как ортогональные проекции точки М на соответствующие оси координат, пишем М(x,y,z). Положение точки М(x,y,z) однозначно определяется ее координатами.