7. Прямая линия на плоскости.

7.1. Понятие уравнения линии на плоскости.

Рассмотрим на координатной плоскости Оху линию l (см. рис. 7.1). Тогда каждая точка М линии l получит координаты х и у, т. е. М(х, у)l.

П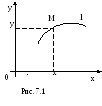од уравнением линии l на плоскости Оху называется уравнение вида

F(x, y)=0, (7.1)

где F(x, y) – функция двух переменных х и у, при этом:

1. координаты точек, лежащих на линии l, удовлетворяют уравнению (7.1),

2. координаты точек, не лежащих на линии l, не удовлетворяют уравнению (7.1).

Обратно. Под линией, определяемой уравнением (7.1), мы понимаем множество точек плоскости Оху, координаты которых удовлетворяют этому уравнению.

Пример 7.1. Проверить, лежат ли точки М₁(3; 0) и М₂(1, 2) на линии l: 4х²+9у²=36.

Решение. Координаты точки М₁ удовлетворяют данному уравнению, т. к. 43²+90²=36, т.е. точка М₁ лежит на данной линии. Точка М₂ не лежит на данной линии, т. к. 41²+92²=40≠36.

7.2 Уравнение прямой на плоскости.

Прямая линия является простейшей линией. Из планиметрии известно, что через две точки проходит единственная прямая. Поэтому для однозначного определения прямой линии необходимо задать два условия. Это будет использовано для вывода различных видов уравнений прямой.

7.2.1 Уравнение прямой с угловым коэффициентом.

Рассмотрим на координатной плоскости Оху прямую l ╫Оу, т. е. не параллельную оси Оу (см. рис. 7.2). Обозначим через φ(0≤φ<π) угол, образованный прямой с положительным направлением оси Ох. Напомним, что углы измеряются против часовой стрелки. Точка К(0,b)- точка пересечения прямой l с осью ординат Оу (см. рис. 7.2). Эти два условия однозначно определяют нашу прямую. Выведем ее уравнение. Из ΔKLN (см. рис. 7.2) ясно, что точка М(х, у) лежит на прямой l тогда и только тогда, когда

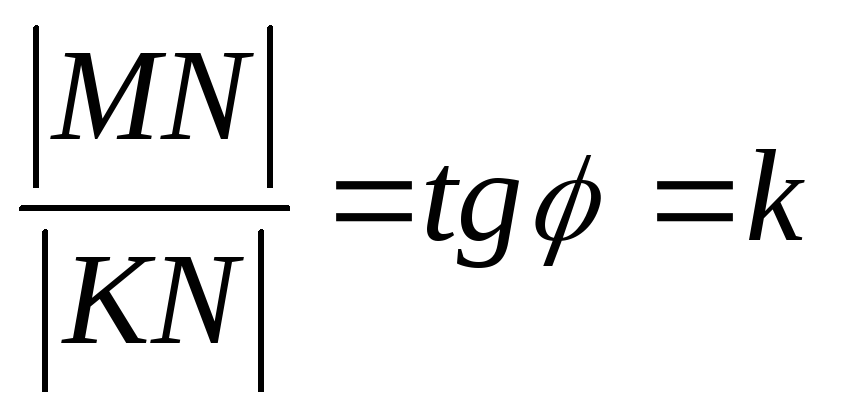, т. е.

число k=tgφ называется угловым коэффициентом прямой, а уравнение

У=kx+b

(7.2)

называется уравнением прямой с угловым коэффициентом.

Если прямая l||Ох, т. е. φ = 0 и к = tgφ = 0, то уравнение (7.2.) принимает вид y = b.

Если прямая проходит через О(0, 0), то b = 0 и уравнение (7.2) примет вид у = кх

Если прямая l||Оу, то φ = и ее уравнение не может быть записано в виде (7.2). Пусть А(а,0) – точка пересечения прямой с осью Ох (см. рис. 7.3). Тогда точка М(х, у) лежит на прямой l тогда и только тогда, когда х = а, т. .е. в этом случае уравнение прямой примет вид

х – а=0. (7.3)

В заключении отметим, что уравнения (7.2) и (7.3) есть уравнения первой степени относительно переменных х и у (координат произвольной точки прямой).

7.2.2. Уравнение прямой, проходящей через данную точку в данном направлении.

Пусть прямая проходит через точку М₀ (х_0, у₀) под углом φ к оси Ох, т.е. с угловым коэффициентом k = tgφ. Точка М(х, у) лежит на прямой тогда и только тогда, когда (см. рис. 7.4):

,

т.е. уравнение прямой примет вид

у-у₀=к(х-х₀)

(7.4)

7.2.3. Уравнение прямой, проходящей через две точки.

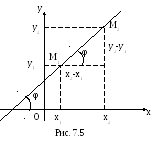
Составим уравнение прямой, проходящей через две точки М₁(х₁, у₁) _и М₂(х₂, у₂) (см. рис 7.5).

Из рис. 7.5 получим, что

Учитывая, что прямая проходит через точку М₁(х₁, у₁), из формулы (7.4) получим уравнения данной прямой

у - у₁ = к(х - х₁), или .

Окончательно, уравнение прямой через две данные точки М₁(х₁, у₁) и М₁(х₂, у₂) примет вид

(7.5)