
1.2 Пример выполнения лабораторной работы №1
Применим методы
численного интегрирования для вычисления
интеграла
 .
.
Задаем число разбиений
![]()
Устанавливаем пределы интегрирования
![]()
Вычисляем шаг сетки
![]()
Вводим подынтегральную функцию

Рассчитываем точное значение интеграла

![]()
Рассчитываем значение интеграла методом левых прямоугольников

Выводим полученное значение
![]()
Выводим значение погрешности в случае использования левых прямоугольников
![]()
Рассчитываем значение интеграла и погрешности методом правых прямоугольников

![]()
![]()
Рассчитываем значение интеграла и погрешности методом центральных прямоугольников

![]()
![]()
Рассчитываем значение интеграла и погрешности методом трапеции

![]()
![]()
Рассчитываем значение интеграла и погрешности методом Симпсона

![]()
![]()
1.3 Варианты заданий к лабораторной работе №1
Примените методы численного интегрирования для вычисления следующих заданий.
1.
 ; 6.
; 6.
 ;
;
2.
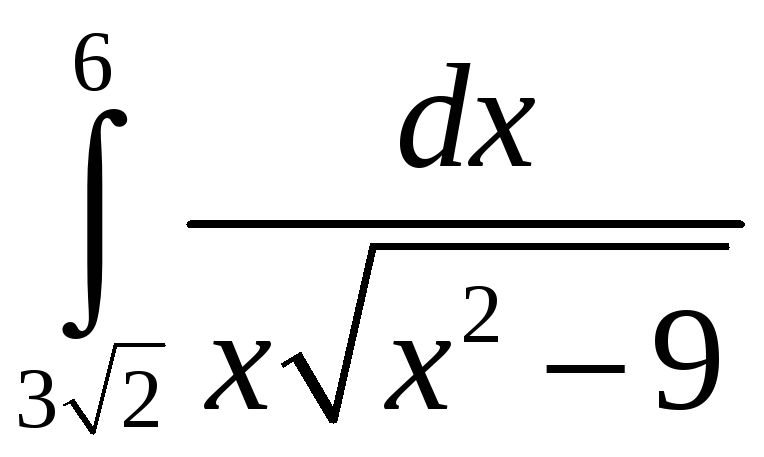 ; 7.
; 7.
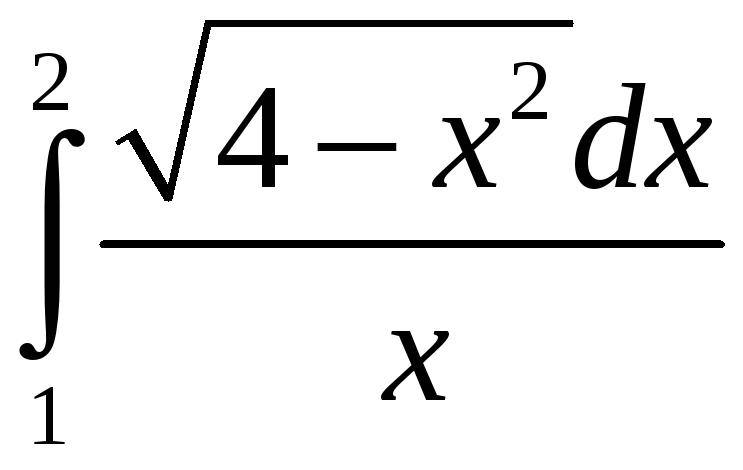 ;
;
3.
 ; 8.
; 8.
 ;
;
4.
 ; 9.
; 9.
 ;
;
5.
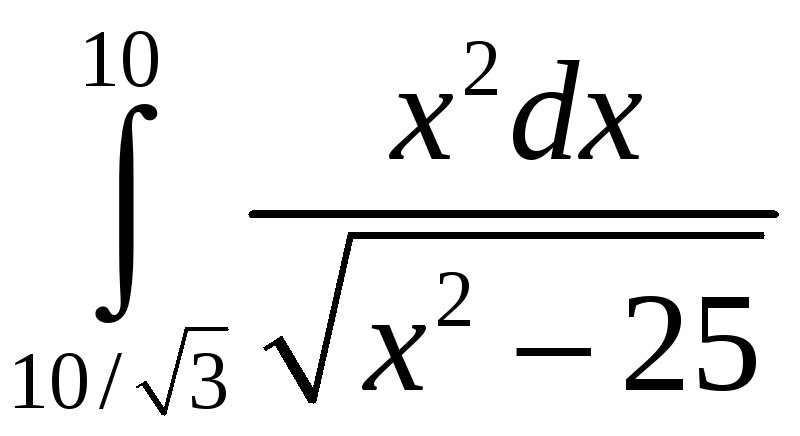 ; 10.
; 10.
 ;
;
Содержание отчета
Отчет должен содержать:
-
титульный лист
-
постановку задачи (согласно варианту)
-
краткое описание методов численного интегрирования
-
программную реализацию данных методов
-
выводы о проделанной работе.
Контрольные вопросы и задания
-
Какие методы численного интегрирования вы знаете?
-
Какой из методов численного интегрирования, в вашем случае, оказался наиболее точным и наименее точным?
-
Чему равна погрешность численного интегрирования для выше изложенных методов?
-
Запишите формулы для приближенного вычисления определенных интегралов.
-
Вычислите определенный интеграл при помощи методов численного интегрирования.
-
Для заданного примера найдите теоретическую и практическую погрешность численного вычисления определенных интегралов.
-
Сравните погрешность методов трапеции и центральных прямоугольников.
-
Как еще называется формула Симпсона и почему?
-
Запишите формулу для расчета погрешности.
10.* Запишите формулу Симпсона через линейную комбинацию формул трапеции и центральных прямоугольников.
