5. Устойчивость.

5.1. Определения устойчивости систем.

Решение для всехi =1,n называется устойчивым по Ляпунову при t  , если для любого действительного существует действительное число, зависящее от, что любое решение, для которого привыполняется неравенство, удовлетворяет неравенствупридля всехi=1,n .

Г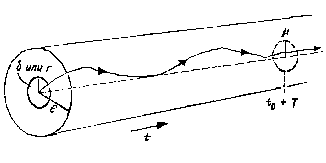еометрически это означает, что все решения , которые приначинаются в – окрестности точки () , никогда не покинут- трубку решения.

Состояние равновесия 0 свободной системы называется устойчивым, если для любого действительного , существует действительное число, такое что при нормевыполняется неравенство.

Другими словами, если состояние равновесия устойчиво, то решение можно выбрать как угодно малым по норме при соответствующем выборе начального условия .

Более сильным является требование достижения в пределе положения равновесия.

Асимптотическая устойчивость

Состояние равновесия 0 свободной системы называется асимптотически устойчивым, если

1. оно является устойчивым,

2) каждое движение, начинающееся достаточно близко от  0 стремится к 0 при .

5.2. Первый метод ляпунова

Рассмотрим свободную систему начало координатявляется

состоянием равновесия, причем это состояние единственное, если . Общее решение уравнения имеет вид- переходная матрица состояния системы.

Необходимым и достаточным условием асимптотической устойчивости в начале координат стационарной свободной системы является требование: действительные части всех собственных значений матрицы А должны быть отрицательны.

Теорема. Состояние равновесия системыасимптотически устойчиво, если состояние равновесиясоответствующей свободной линейной стационарной системы, асимптотически устойчиво.

Существует также аналогичная теорема о неустойчивости.

Теорема. Состояние равновесия системынеустойчиво, если состояние равновесиясоответствующей свободной линейной стационарной системы, неустойчиво.

Пример 1. Рассмотрим свободную систему

, 0 является точкой равновесия.

Линеаризованная система имеет вид

. Получим характеристическое уравнение .

Собственные числа матрицы А есть

.

Если k>0 , то начало координат является асимптотически устойчивым положением равновесия для исходной системы, так как оно асимптотически устойчиво для линеаризованной системы. Если k<0 , то исходная система неустойчива.

Пример 2.

У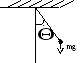равнение колебаний незатухающего простого маятника.

Перейдя к системе уравнений первого порядка, получим уравнения состояния

где k – постоянная, зависящая от длины маятника ( k=g/l ).

Для этой системы начало координат является состоянием равновесия и соответствующая линейная система имеет вид

.

Так как собственные числа являются чисто мнимыми, первый метод Ляпунова не дает информацию об устойчивости состояния системы ( отметим, что начало координат является устойчивым, но не асимптотически устойчивым).

Теперь предположим, что имеется затухание колебаний вследствие трения. Тогда уравнение 2-го порядка имеет вид

,

с- коэффициент затухания.

При исходное уравнение представляется в виде системы уравнений

Начало координат является состоянием равновесия.

В результате линеаризации получаем

Так как действительные части собственных чисел

отрицательны, то начало координат является асимптотически устойчивым положением равновесия, а следовательно, и исследуемая нелинейная система имеет асимптотически устойчивое положение равновесия в начале координат.

ЛІТЕРАТУРА

1. Иванов В.А. Математические основы теории регулирования. Учебное пособие для втузов. М., Высшая школа, 1971.

2. Директор С., Рорер Р. Введение в теорию систем, изд - во «Мир», 1974.

3. Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления. М., Высшая школа, 1988.

4. Арнольд В. И. Обыкновенные дифференциальные уравнения, изд-во «Наука», М„ 1971.

5. Бахвалов Н. С. Численные методы (Анализ, алгебра, обыкновенные диф­ференциальные уравнения), изд-во «Наука», М., 1973.

6. Бусленко Н. П., Калашников В. В., Коваленко И. Н. Лекции по теории сложных систем, изд-во «Советское радио», М., 1973.

7 Демидович Б. П. Лекции по математической теории устойчивости, изд-во «Наука». М., 1967.

8 Зубов В. И. Методы А. М. Ляпунова и их применение, изд-во МГУ, 1957.

9. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем, изд-во «Мир», М., 1971.

10. Канторович М. И. Операционное исчисление и процессы в электрических полях, изд. 3-е, изд-во «Наука», М., 1964.

11. Колмогоров А. Н., Фомин С. В. Элементы теории функции и функциональ­ного анализа, изд. 3-е, изд-во «Наука», М., 1972.

12. Ройтенберг Я. Я. Автоматическое управление, изд-во «Наука», М., 1971.

Учебное издание