4. Решения линейных систем n-го порядка.

4.1. Общее решение однородной линейной системы n-го порядка.

Рассмотрим однородную линей­ную систему уравнений

(1)

Здесь А есть n  n квадратная матрица коэффициентов урав­нений;

x(t) - матрица-столбец (вектор) из неизвестных функций.

Будем искать общее решение системы (1) в виде

, (2)

где должны быть определены.

Подстановка решения (2) в уравнение (1) дает

(2)

После сокращения на ненулевой скаляр получаемили

, (3)

где I- единичная матрица размером n n.

Для решения системы (1) необходимо решить систему алгебраических уравнений (3).

Следовательно, вектор х, определенный соотношением (2), является решением системы, если есть вектор собственных значений иесть соответствующие собственные вектора матрицыА.

Пример.

Найти общее решение системы , где

.

Формируем систему алгебраических уравнений (4) .

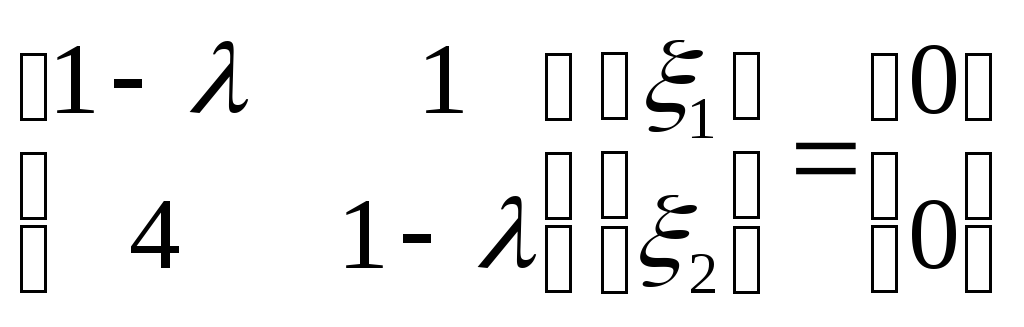Находим корни характеристического уравнения .

Соответствующие собственные вектора: для _{1 ,} для _{2 .}

Тогда общее решение системы есть

.

4.2. Решение неоднородной линейной системы.

Рассмотрим уравнение состояния стационарного управляемого объекта

. (1)

Пусть S есть матрица, образованная собственными векторами матрицы А. Определим новую зависимую переменную y как

x=Sy . (2) .

Подставляя (2) в уравнение (1), получим

.

Умножая на S^-1 получим

, (3)

где иD есть диагональная матрица, образованная собственными значениями матрицы А .

Уравнения (3) представляют собой систему несвязанных уравнений . Эти уравнения могут быть решены отдельно.

В скалярной форме уравнения (3) имеют форму

i=1,n (4)

где - есть определенная комбинация .

Решение для уравнений (4) имеют вид

, i=1,n, (5)

где с –произвольная константа.

Наконец, используя результат (5), решение x(t) исходного уравнения (1) можно получить используя соотношение (2).

4.3. Понятие о канонической форме Жордана.

Не всякую матрицу можно привести линейным преобразованием к диагональному виду. Удобно выделить класс матриц простейшего вида, к которому можно было бы привести путем некоторых линейных преобразований любую матрицу.

Рассмотрим квадратную матрицу размера п х п, элементы главной диагонали которой равны числу о, элементы а 1(i =1, 2, ....n-1) единицы, а все остальные элементы - нули:

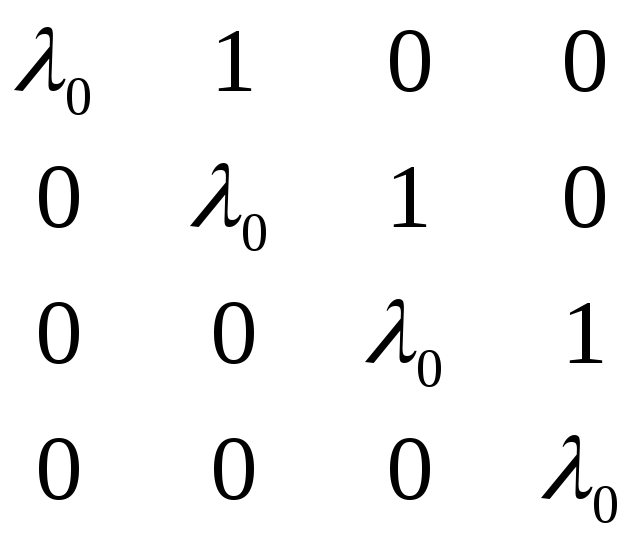
Такая матрица называется клеткой Жордана порядка n, отвечаю­щей собственному значению o.

Жордановой матрицей называется клеточно-диагональная матрица, в которой на главной диагонали стоят клетки Жордана, а все эле­менты вне этих клеток равны нулю.

Например, матрица

является жордановой матрицей, состоящей из пяти клеток: -двух клеток второго порядка, отвечающих собственному значению 2, -клетки третьего порядка и клетки первого порядка, отвечающих собственному значению 3, -и клетки первого порядка, отвечающей собственному значению 1.

Справедлива приводимая без доказательства теорема о приве­дении матриц к жордановой форме.

Теорема . Для всякой числовой матрицы А существует по­добная ей жорданова матрица J,

т. е. существует такая невы­рожденная матрица С, что .

Матрица J составлена из клеток Жордана, отвечающих собствен­ным значениям матрицы A. Заметим, что одному и тому же соб­ственному значению может соответствовать несколько клеток Жордана различного размера.

Матрицы, записанные в жордановой форме, используются в даль­нейшем при изучении систем линейных дифференциальных уравне­ний с постоянными коэффициентами.

4. Решение однородной линейной система уравнений (общий случай).

Рассмотрим однородную линей­ную систему уравнений . В общем случае матрицуА можно с помощью невы­рожденного преобразования привести к жордановой форме, т. е. существует такая невырожденная матрица С, что . Здесь J — жорданова форма матрицы А. Для приведе­ния матрицы A к жордановой форме сделаем замену неизвестных функций. Положим х = Су, где C - некоторая невырожденная матрица, . Тогда

или

Умножая обе части равенства (3) слева на , получим

,

Жорданова матрица

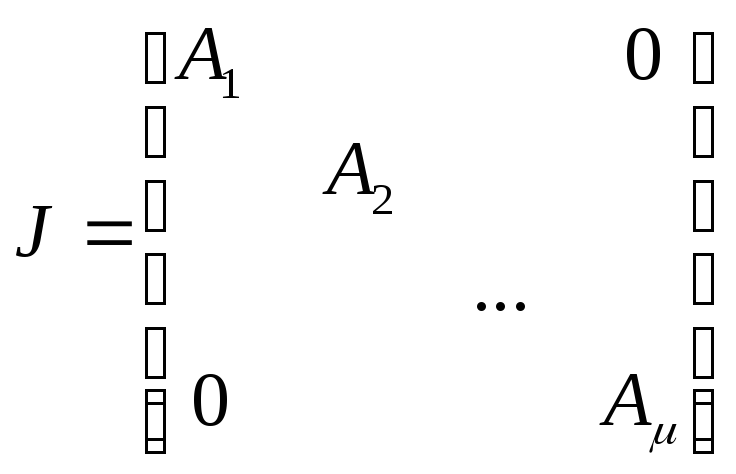
состоит из клеток A_l , имеющих следующую структуру:

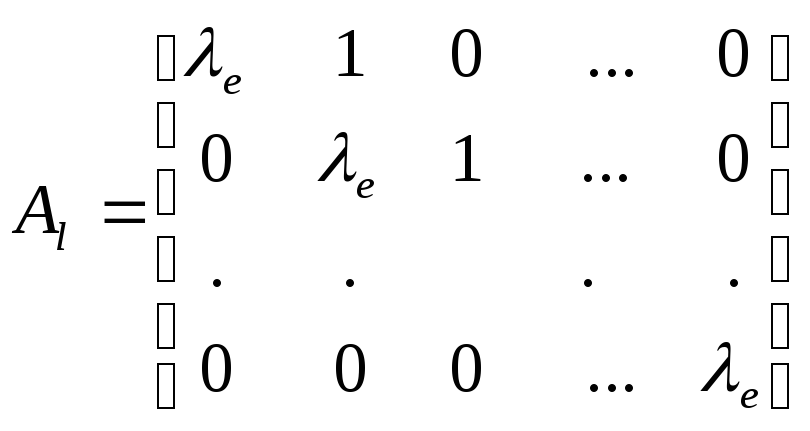
где _l - характеристическое число матрицы A.

Обозначим размерности клеток соответственно е₁ , е₂ ..., e_.. Тогда исходную систему уравнений можно записать в развернутом виде





. . . . . . . . . . . .  (1)

__ __ __ __ __ __ __ __ __ __ __  __ __ __ __ __ __ __ __ __



. . . . . . . . . . . . . . . . . . . . . 



Каждой клетке жордановой матрицы J соответствует подсистема дифференциальных уравнений. Первая подсистема системы (1) содержит е₁ уравнений, в которые входят только первые е₁ неизвестных и не входят неизвестные из других подсистем. И вообще, в любую из подсистем системы (1) не входят неизвестные y_i; из других подсистем, поэтому каждую подсистему можно решать независимо от других.

Чтобы решить первую подсистему, сделаем замену переменных

(2)

. . . . . .

тогда получим первую подсистему в виде

, , . . . , (3)

Подсистема (3) легко решается, если начинать решение с последнего уравнения. Действительно, интегрируя с конца, получим

, , .

Переходя по формулам (2) к переменным у_i получим решение первой подсистемы в виде

,

,

. . . . . . . . . . . . . .

.

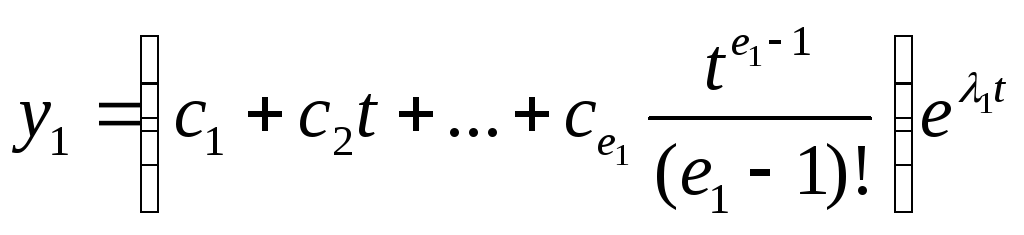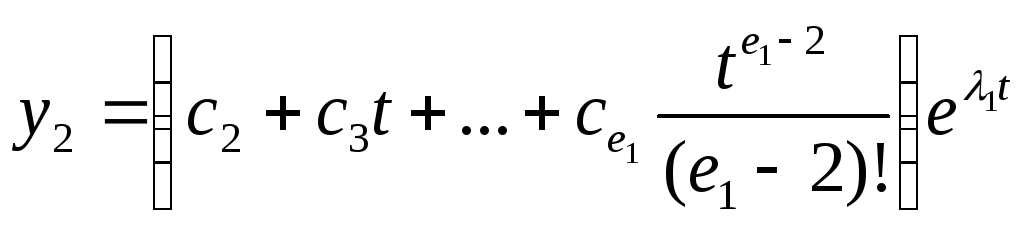При интегрировании появились произвольные постоянные , число которых равно е₁. Решение остальных подсистем записы­вается аналогично. Напишем решение для последней подсистемы:

,

,

. . . . . . . . . . . . . .

,

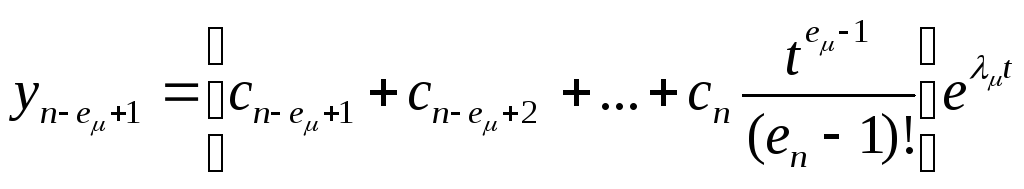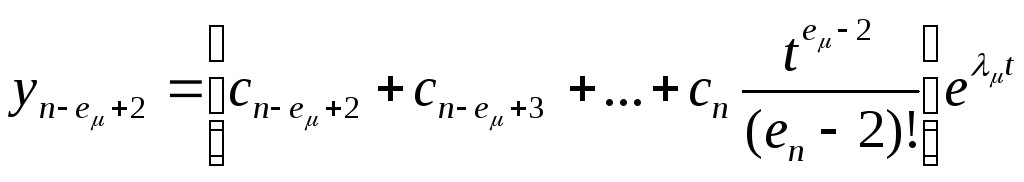где , … ,- произвольные константы.

3. Фундаментальная матрица однородной системы.

Фундамен­тальная матрица линейной однородной системы уравнений с постоян­ными коэффициентами имеет вид

Выявим структуру экспоненциальной матрицы .

Пусть матрица А приведена к жордановой форме, т. е. имеет вид

,

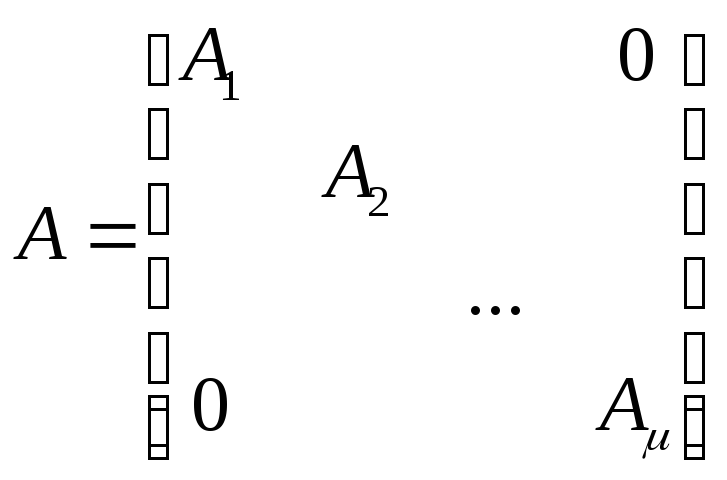где клетка А_i , соответствующая характеристическому числу

,

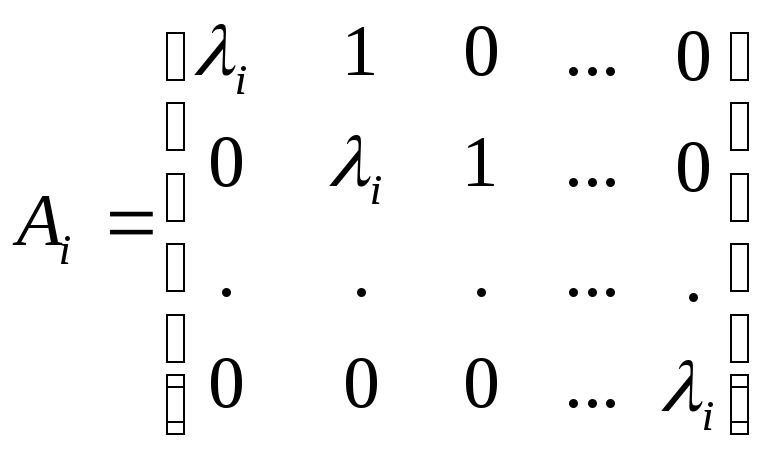есть квадратная матрица размера e_i  e_i . Рассмотрим частный слу­чай, когда t₀=0. Тогда является фундаментальной матрицей решений системы (1), причем Х(0)=Е. Нетрудно пока­зать, что

,

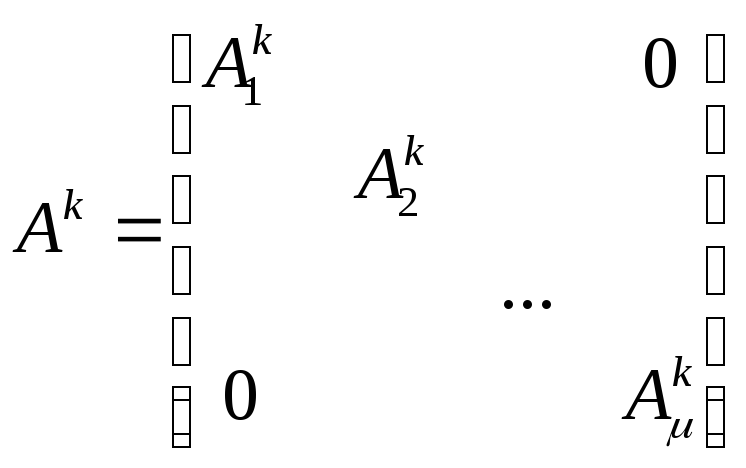Действительно, последнее равенство непосредственно следует из правила умножения матриц. Тогда можно написать:

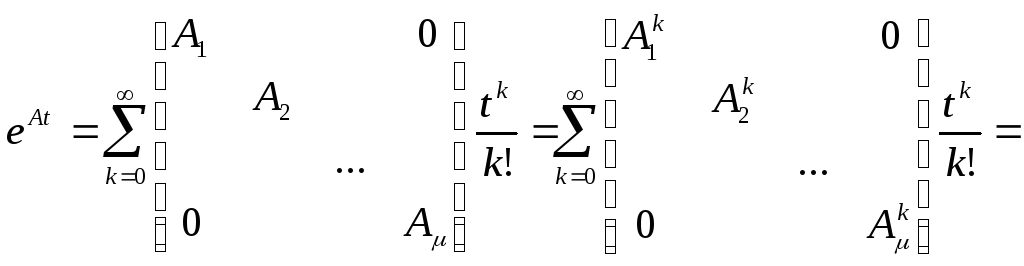
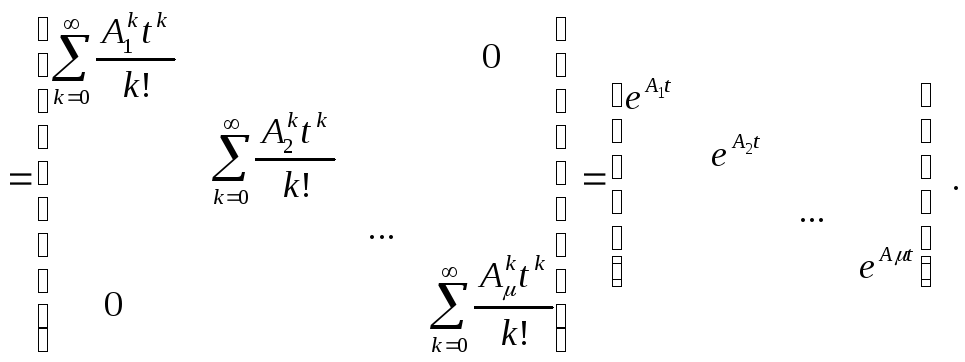
Таким образом, если матрица А имеет жорданову форму, то

.
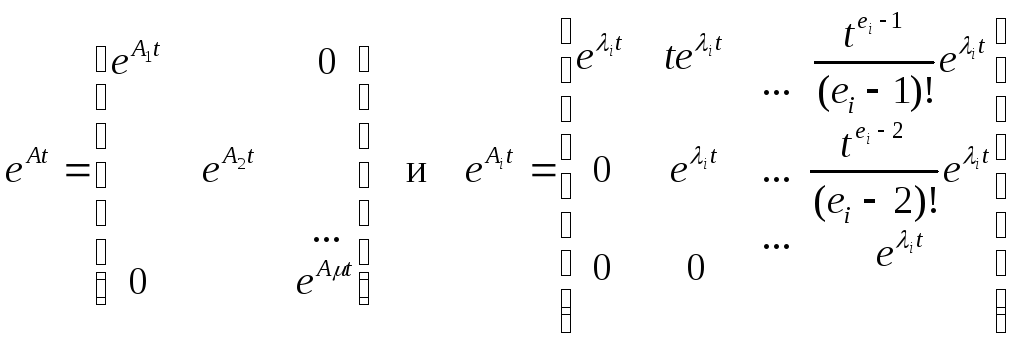