3.3. Теорема кели-гамильтона

Каждая квадратная матрица порядка n удовлетворяет своему характеристическому уравнению,

т.е. если , то

С помощью основного результата теоремы можно вычислить любую положительную целую степени матрицы А через первые n-1 степеней матрицы.

Аналогично можно найти обратную матрицу, имея соотношение , раскроем скобки, разрешим относительноА^-1 - это выражение имеет смысл, если только, что эквивалентно условию существования обратной матрицы.

ПОНЯТИЕ ФУНКЦИИ ОТ КВАДРАТНОЙ МАТРИЦЫ

Пусть задана скалярная функция и мы хотим получить соответствующую матричную функцию квадратной матрицы А порядка n.

Определим функцию от матрицы через степенной ряд -k- тая производная:

,

предполагая, что матричный ряд сходится.

Второй способ представления функции матрицы А с различными собственными значениями можно определить через скалярные функции на каждом одномерном инвариантном подпространстве: гдесобственные вектора.

Поэтому существует, если существует .Используя теорему Кели –Гамильтона

можно упростить вычисления матричной функции, т.е. ее можно представить в виде конечной суммы , отсюда

.

Следовательно

Мы получили n уравнений от n неизвестных коэффициентов . Эти уравнения можно переписать в виде матричного уравнения

.

Определитель Вандермонда не равен 0 тогда и только тогда, когда собственные значения различны (что и предполагалось).

Пример. Дана матрица

Так как n=2 имеем: Получаем систему относительно :

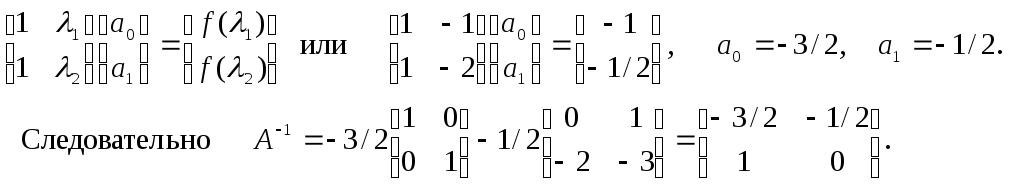
Функция представляет интерес при изучении систем второго и более высокого порядка. Рассмотрим пример вычисленияс помощью теоремыКели -Гамильтона.

Вичислить функцию .

По теореме Кели -Гамильтона

Составляем систему

.	Решая эту систему получаем

3.4. Привидение матрицы к диагональному виду

Рассмотрим матричное соотношение . Пустьбазис собственных векторов, соответствующих собственным значениям, предположим, что в этом базисе представлены векторx и y

.

Тогда соотношение преобразуется к виду

.

Т.к. собственные векторы линейно независимы, тодля.

Если матрица А не вырождена, т.е. дляk=1..n и координаты х просто

выражаются через y . Поэтому в базисе собственных векторов линейное преобразованиеТ, соответствующее матрице А в первоначальном базисе представляется матрицей

или

Весь набор характеристических корней называется спектром линейного преобразования Т. Говорят, что преобразование Т имеет простой спектр, если все корни действительны и различны.

Во многих случаях необходимо знать - может ли данное линейное преобразование Т иметь диагональную матрицу. Всякое линейное преобразование с простым спектром может быть задано диагональной матрицей. Получаем следующий результат: всякая матрица, у которой все характеристические корни действительны и различны, подобна диагональной матрице, или такая матрица приводится к диагональному виду.

Предположим, что столбцы матрицы S образована собственными векторами . Матричное соотношениепреобразуется в новом базисе к видуили, где векторх в базисе собственных векторов имеет вид , аналогично.

Рассмотрим сначала .

В базисе собственных векторов матрица А может быть преобразована к диагональному виду

следующим преобразованием

Пример

.

Если S - матрица, приводящая матрицу А с различными собственными значениями к диагональному виду, то . СледовательноПоследнее соотношение можно переписать в виде, где- базис собственных векторов, а- соответствующий взаимный базис.

В частности .