1.3. Общее решение линейного уравнения первого порядка

Получим общее решение линейного уравнения первого порядка в стандартной форме:

(1)

Рассматриваем соответствующее однородное уравнение (с нулевым входным воздействием)

(2)

Разделяем переменные

(3)

Проинтегрировав его от  до t , получаем

(4)

Если начальное условие задается в момент времени t₀ , решение имеет вид

, (5)

где начальное условие есть некоторая константа .

Для получения частного решения линейного неоднородного уравнения применим метод вариации произвольной постоянной. Ищем решение уравнения (1) в том же виде (5), что и решения соответствующего однородного уравнения только с придется рассматривать не постоянной, а зависящей от t, и должна быть такой, что при подстановке решений иdx/dt в исходное уравнение (1) оно обращалось в тождество.

Пусть (t) определяет однородное решение уравнения (1) так, что

. (6)

Ищем частное решение в виде

. (7)

Подставим выражения (7) в уравнение (1)

Учитывая (6), получим или

(8)

Проинтегрируем выражение (8) и результат умножим на (t), получим

.

(заметим, что ).

Поскольку ,

есть решение однородного уравнения, то частное решение можно записать в виде

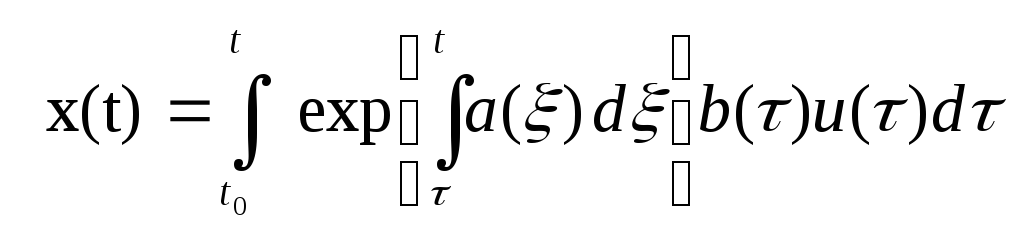, (9)

Общее решение находится как сумма решения однородного уравнения и рассматриваемого частного решения

+ . (10)

Пример

-линейное неоднородное уравнение.

Решаем сначала линейное однородное уравнение

Получаем решение

Ищем частное решение данного уравнения в виде: ,

тогда

Подставляем y и dy/dt в исходное уравнение

После приведения подобных получаем

, ,где с₁- произвольная константа.

Общее решение данного уравнения имеет вид:

1.4. Представление уравнений состояния в виде блок-схем

Стандартная форма приведения системы

Систему удобно описывать графически в виде блок-схем, для большинства систем основными линейными блоками является сумматор, счетчик, интегратор.

Сумматор

Счетчик

Интегратор

Эти элементы линейны.

Уравнения системы первого порядка в стандартной форме с одним входом и одним выходом могут быть представлены в виде блок схемы:

1.5. Понятия теории устойчивости

Рассмотрим нелинейную нестационарную систему n-го порядка

. (1)

Если u  0, то система называется свободной.

Решение системы однозначно определяется начальным состоянием и его можно

записать в виде Подставляя решение в исходную систему, получим

Функция называется переходной функцией состояния системы.

Пусть задана свободная система . Состояниеназываетсясостоянием равновесия, если или (что то же самое )

) .

Дифференциальное уравнение называется стационарным, если

при любых . Стационарность означает, что правая часть не зависит в явном виде от времени.

Свободную систему, описываемую стационарным дифференциальным уравнением, будем называть автономной.

Рассмотрим следующие два вопроса:

- будет ли решение уравнения (1) для входной функции u(t) и заданного начального состояния устойчиво при соответствующем отклонении от начального состояния?;

­­- для нулевой входной функции u(t)=0 устойчиво ли состояние равновесия?.

Рассмотрим систему при небольших отклонениях в начальном состоянии.

, (1)

где -мера некоторого отклонения одной траектории от другой.

В момент отклонение имеет вид

Устойчивость решения может быть установлена по изменению .

Если для малых , т.е. для малого сдвига в начальном состояниистанет большой при увеличении, то решение называется неустойчивым, т.к.расходится с. Если жес возрастанием, то тогда решение можно назватьасимптотически устойчивым.

Механическая интерпретация

Из выражения (1) получаем

где - переходная функция процесса.

Но x(t) есть решение уравнения такое, что

или

(2)

т.к.

Поскольку входная переменная u и решение Ф известны, то правая часть выражения (2) является только функцией ,

.

Заметим, что , есть состояние равновесия, поскольку.

Таким образом, проблема определения устойчивости решения сведена к проблеме устойчивости состояния равновесия, порожденного однородным дифференциальным уравнением.

УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ

При исследовании состояния равновесия будем предполагать, что входная переменная . Рассмотрим систему

.

Предположим, что эта система находится в состоянии равновесия в точке ,

тогда .

Отклонение от этой точке можно найти через

положение равновесия в начале координат.

Мы показали, что устойчивость состояния равновесия также может быть исследована с помощью некоторой однородной системы, имеющую состояние равновесия в начале координат.

Рассмотрим систему первого порядка

,

для которой является единственным состоянием равновесия.

Решение этого уравнения есть

Если , то и само решение равно 0.

Если , то рассматривается 3 случая, в зависимости от коэффициентаa .

1)-начальное состояние являетсяасимптотически устойчивым состоянием равновесия;

2) - начальноесостояние устойчиво.

3) - начальноесостояние будет неустойчивым состоянием равновесия.