
- •Глава I. Случайные события. Вероятность
- •Вероятность случайного события
- •1.3.1. Несовместные случайные события. Теорема сложения вероятностей
- •1.3.2. Независимые случайные события. Теорема умножения вероятностей
- •1.3.3. Зависимые события. Теорема умножения вероятностей для зависимых событий
- •1.4. Формула Байеса
- •Глава II. Случайные величины
- •2.1. Случайные величины, их виды
- •2.2. Закон распределения дискретной случайной величины
- •2.3. Закон распределения непрерывной случайной величины. Плотность распределения вероятности
- •2.4. Основные числовые характеристики случайных величин
- •2.5. Нормальный закон распределения случайных величин
- •Глава III Элементы математической статистики
- •3.2. Статистическое распределение выборки
- •3.3. Графическое представление статистических распределений выборок
- •3.4. Методы описательной статистики
- •3.5. Оценка параметров генеральной совокупности по ее выборке.
- •3.6. Понятие нормы для медицинских показателей
2.4. Основные числовые характеристики случайных величин
Рассмотрим характеристики положения – математическое ожидание, моду, медиану.
Математическое
ожидание М(Х)
случайной величины Х
является вероятностным аналогом ее
среднего арифметического
![]() (М(Х)
=
(М(Х)
=
![]() или
М(Х)
или
М(Х)
![]() ).
).
Для дискретной случайной величины М(Х) вычисляется по формуле:
М(Х)
= х1р1
+ х2р2
+…+ хnрn
=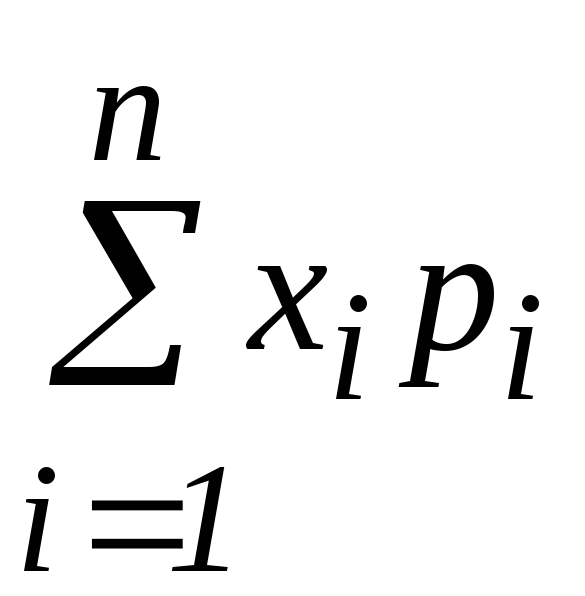 .
(18)
.
(18)
Для непрерывной случайной величины М(Х) определяют по формулам:
М(Х)
=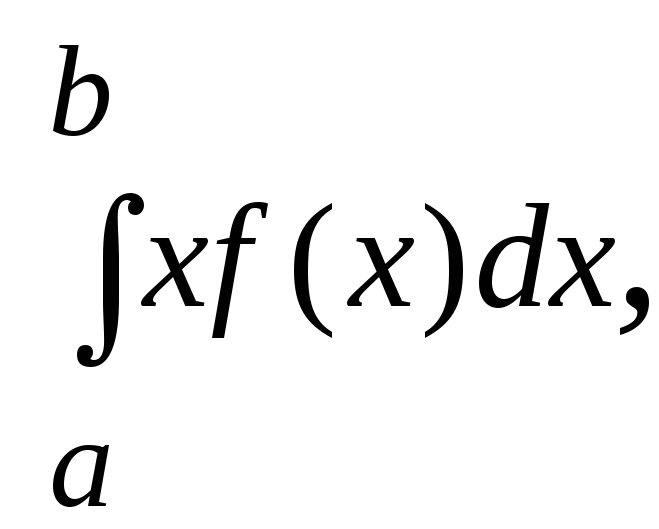 или М(Х)
=
или М(Х)
=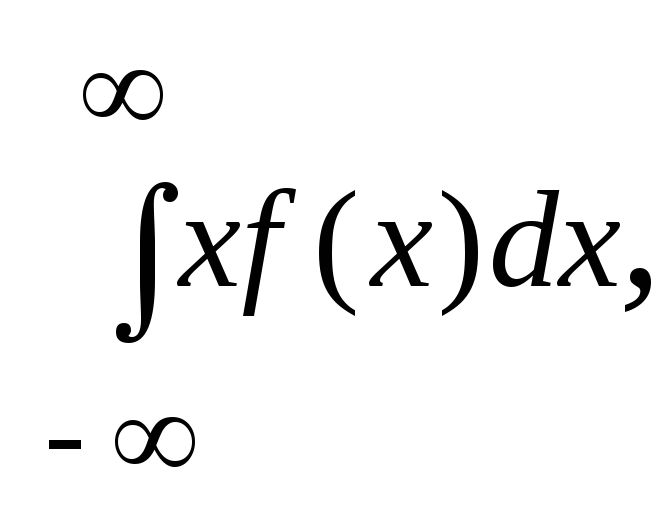 (19)
(19)
где f(x) – плотность вероятности, dP = f(x)dx – элемент вероятности (аналог pi для малого интервала x (dx)).
Пример: Вычислите среднее значение непрерывной случайной величины, имеющей на отрезке (a, b) равномерное распределение.
Решение: при равномерном распределении плотность вероятности на интервале (a, b) постоянна, т.е. f(х) = fo = const, а вне (a, b) равна нулю; из условия нормировки (15) найдем значение f0:
![]()
 =
f0
=
f0
![]() =
f0
x
=
f0
x
![]() = (b-a)f0
, откуда
= (b-a)f0
, откуда
![]()
Поэтому:
M(X)
=
![]()
![]() =
=
![]() =
=
![]() (a
+ b).
(a
+ b).
Следовательно,
математическое ожидание М(Х) совпадает
с серединой интервала (a,
b),
определяющей
![]() ,
т.е.
,
т.е.
![]() = M(X)
=
= M(X)
=
![]() .
.
Модой Мо(Х) дискретной случайной величины называют ее наиболее вероятное значение (рис.4а), а непрерывной – значение Х, при котором плотность вероятности максимальна (рис.4б).
Медианой (Ме) случайной величины обычно пользуются только для непрерывных случайных величин, хотя формально ее можно определить и для дискретных Х. Медианой Ме(Х) случайной величины называют такое значение Х, которое делит все распределение на две равновероятные части, т.е. вероятности Р(Х Ме) и Р(Х Ме) оказываются равными между собой:
Р(Х
< Ме)
= Р(Х
> Ме)
=
![]() .
.
Поэтому медиану можно вычислить из соотношения:
![]() =
=![]() .
.
Графически медиана – это значение случайной величины, ордината которой делит площадь, ограниченную кривой распределения, пополам: S1 = S2 (рис. 4в).
Если М(Х), Мо(Х) и Ме(Х) совпадают, то распределение случайной величины называют симметричным, в противном случае – асимметричным.
Характеристики рассеяния – это дисперсия и стандартное отклонение (среднее квадратическое отклонение)
Дисперсия D(X) случайной величины Х определяется как математическое ожидание квадрата отклонения случайной Х от ее математического ожидания М(Х):
D(X) = M[X – M(X)]2 , (20)
или D(X) = M(X2 ) – [M(X)]2 . (21)
При конкретных расчетах для дискретной случайной величины эти формулы записываются так:
D(X)
=![]() [хi–М(Х)]2
рi
, или
D(X)
=
[хi–М(Х)]2
рi
, или
D(X)
=![]() хi2
рi
– [M(X)]
2
(22)
хi2
рi
– [M(X)]
2
(22)
Для непрерывной случайной величины, распределенной в интервале (a,b), они имеют вид:
D(X)
=![]() [x–M(X)]
2
f(x)dx,
или D(X)
=
[x–M(X)]
2
f(x)dx,
или D(X)
=![]() х2
f(x)dx
– [M(X)]2,
(23)
х2
f(x)dx
– [M(X)]2,
(23)
а для интервала (-∞,+∞):
D(X)=![]() [x–M(X)]2
f(x)dx,
или
D(X)=
[x–M(X)]2
f(x)dx,
или
D(X)=![]() х2
f(x)dx–
[M(X)]2.
(24)
х2
f(x)dx–
[M(X)]2.
(24)
Однако дисперсия D(Х) имеет размерность квадрата случайной величины, что весьма неудобно при оценке разброса в физических, биологических, медицинских и других приложениях. Поэтому обычно пользуются параметром, размерность которого совпадает с размерностью Х. Это – среднее квадратическое (иначе – стандартное) отклонение случайной величины Х, которое обозначают (Х):
(Х)
=
![]() .
(25)
.
(25)
