Ответ: 5,0 м/с.

Р

9. Дано:   m1 = 10 г = = 10–2 кг m2 = 5 кг l = 4 м α = 25˚

Vпули – ?

ешение

Рассмотрим состояния системы в моменты, когда маятник с пулей был в точках 1 и 2. В точке 1 пуля попала в маятник. Система имела скорость V,

Е_к1 = , Е_р1 = 0. В точке 2 V = 0, Е_к2 = 0,

Е_р2 = . Согласно закону сохранения энергии

= (1).

Удар опишем с помощью закона сохранения импульса (2). Высоту подъема маятника h определим из формулы cos α = Из уравнений (1) – (3) находим скорость пули

, V_пули = 1400 (м/с)

Ответ: 1400 м/с.

Р

10. Дано:    t, A, V0, m

h – ?

ешение

Ответ:

Р

11. Дано:    m, l, α, m1, μ

h – ?

ешение

Лестница не вращается, следовательно, сумма моментов сил, вращающих лестницу относительно оси, проходящей через точку A, равна 0:

(1), АС = (2).

Так как ускоренное поступательное движение отсутствует, то a_x = 0 и a_y = 0. Следовательно, N₂ = F_тр (3) и (4), при этом (5).

Из уравнений (1)–(5) получим

.

Ответ: .

Р

12. Дано:    h = 2,0  10–2м S = 2,00  10–2 м2 л = 0,90  103 кг/м3

m – ?

ешение

Условие плавания льдины (1), где V₁ – объём части льдины, погружённой в воду.

(2), где V – объем всей льдины, так что V = Sh (3). (4), V_H – объём надводной части. Из уравнений (1) – (4) получим

 , , m = 3,6 кг.

Ответ: 3,6 кг.

Вариант 8

Р

1. Дано:    = 30 u = 18 км/ч = = 5 м/с

V – ? Vв – ?

ешение

Обозначим скорость трамвая относительно Земли , скорость воз­ду­ха относительно Земли – это скорость ветра, обозначим . – скорость капли относительно Земли в безветренную погоду. Очевидно, такова же скорость капли относительно воздуха, так что . Скорость капли относительно трамвая . Из теоремы сложения скоростей следует, что (1), а также (2). Из рисунка следует, что при движении трамвая:  ,

V  8,7 м/с.

Из уравнений (1), (2) получаем:  V_в = u = 5 м/с.

Ответ: 8,7 м/с, 5,0 м/с.

Р

2. Дано:

V0, V – ?

ешение

 ; , ,

Ответ: 12 м/с, 28 м/с.

3. Дан график а_х(t); при t = 0 V_x = 5 м/с, x = 0.

Решение

На интервалеc:

а_х = – 1 м/с², x(0) = 0, V(0) = 5 м/с, V(t) = 5 – t, м/с, V(10) = – 5 м/с;

x(t)= 5t – 0,5 t² (м), x(10) = 0,

х(5) = 12,5 м.

l(10) = 2  12,5 = 25 м.

На интервале с:

а_х = 0 м/с², x(10) = 0 м, V(t) = – 5 м/с;

x(t) =  – 5(t – 10) (м), x(20) = – 50 м. l(20) = l(10) + 50 = 75 м.

На интервале с:

V(20) = – 5 м/с, а_х = 1 м/с²,

V(t) = – 5 + 1·(t – 20),

V(30)= – 5 +10 = 5 (м/с)

x(t) = – 50 – 5(t – 20) + 0,5(t – 20)², м

х (30) = – 50 м, x(25)= – 62,5м,

l(30) = l(20) + 25 = 100 м.

На интервале с графиком пути будет парабола, ветви которой направлены вниз, так как движение равнозамедленное. На интервале с графиком пути будет парабола, ветви которой будут направлены вверх, так как движение на данном участке равноускоренное. На интервале с график пути – прямая линия, так как движение равномерное. На интервале с графиком пути будет парабола, ветви которой направлены вниз, так как движение равнозамедленное. На интервале с графиком пути будет парабола, ветви которой направлены вверх, так как движение равноускоренное.

4. Дано: V0 = 28 м/с h = 0,50 hmax g =10 м/с2

t – ?

Решение

 .

Для определения h_max используем формулы кинематики. Так как время подъема равно времени падения, t_вверх = t_вниз = t_m, в верхней точке траектории скорость равна 0, то

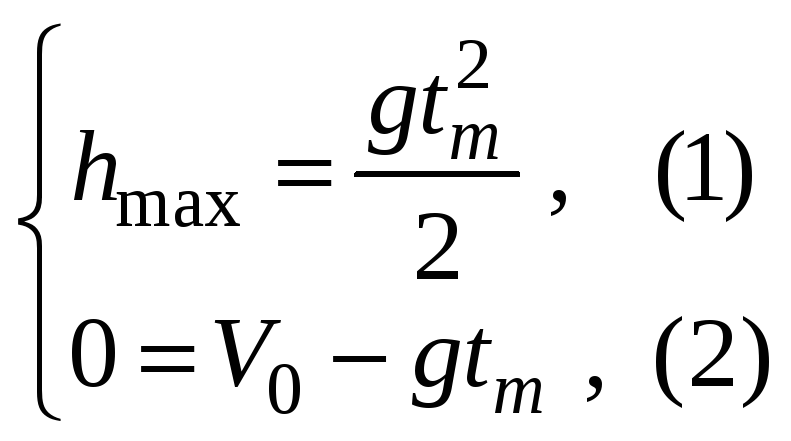Из уравнений (1) и (2) получим .

, , , .

В точку h = 0,50 h_max тело попадает дважды, считаем, что тело достигнет заданной высоты при

Ответ: 0,82 с.

Р

5. Дано: ν = 10,0 с–1 S = 0,300 м φ = 9000,157 рад.

V – ?

ешение

Скорость пули между дисками , за это время первый диск повернётся на угол φ, вращаясь с угловой скоростью.

Поэтому , , V = 120 м/с.

Ответ: 120 м/с.

Р

6. Дано: m, α, l, t

N, Fнат – ?

ешение

Обозначим:  – линейная частота вращения,  – угловая скорость вращения, V – линейная скорость движения по окружности, a – центростремительное ускорение мальчика. Тогда

Из уравнений (1)–(4) получаем

(5)

По III закону Ньютона

Опишем движение мальчика, используя II закон Ньютона в векторной форме .

В скалярной форме

х: , (6)

у: . (7)

63