Инвариантность формы 1-го порядка.

Th. u = u(x) -дифференцируема в точке х, а функция y = f(u) - дифференцируема в точке u = u(x). Тогда дифференциал от сложной функции d(f(u(x)))

d(f(u)) = f’(u)du (1)

df(u) = d(f(u(x))) = (f(u(x)))’_xdx = f’_u(u)*u’_x(x)dx = f’_u (u)du 

Эта теорема показывает, что форма не меняется от замены независимой переменной на дифференцируемую функцию от х.

Дифференциалы высших порядков уже не обладают свойством инвариантности (доказать самим).

Применение дифференциального исчисления к исследованию функций.

Основные теоремы дифференциального исчисления.

Def.1 Пусть f: ER и точка х₀ Е. Точка х₀ называется точкой локального максимума (минимума), если  U(х₀, E) := U(х₀)  E :  x U(х₀, E)  f(x)  f(х₀) (f(x)  f(х₀))

Def.2 Пусть f: ER и точка х₀ Е. Точка х₀ называется точкой строгого локального максимума (минимума), если  U(х₀, E) := U(х₀)  E :  x U(х₀, E)  f(x) < f(х₀) (f(x) > f(х₀))

Def.3 Точки локального максимума (минимума) называются точками эстремумов функции f(x), а значения f(x)- эстремумами.

Def.4 Точка х₀ называется внутренним локальным экстремумом функции f: ER, если

1. х₀  Е

2. х₀–предельная точка для 2-х множеств: U⁺ (х₀, E):= (a, х₀ )  E

U^- (х₀, E):= (х₀, b )  E

Пример: f(x) = x²; -1  x  1 E = [-1, 2)

1; 12 , 2

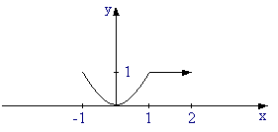
точка х = (-1) – точка строгого локального максимума

точка х = 0 – точка строгого локального внутреннего минимума

точка х = 1 - точка локального внутреннего максимума

точки 1 < x < 2 – точка внутреннего максимума и минимума одновременно

точка х = 2 не является точкой строгого локального максимума

Th. (теорема Ферма)

Пусть f: ER, точка х₀– точка внутреннего локального экстремума, если f(x) – дифференцируема в точке х₀, то f’(х₀) = 0.

f = f(х₀ + h) – f(х₀) = f’(х₀)*h + ō(h) = [f’(х₀) + ō(1)] * h (1)

от противного: т.е. правая часть равенсва (1) при h достаточно близких к 0 сохраняет знак производной  при изменении знака h (при условии, что х₀+h  E)

правая часть (1) меняет знак, что невозможно, поскольку, если точка х₀– точка максимума функции, то левая часть (1) не положительна в окресности U(х₀, Е), а если минимума, то левая часть (1) – неотрицательна в той же окресности  левая часть менять знак не может, а правая при изменении h меняет знак  противоречие.

Для точки внутреннего экстремума h может быть больше и меньше 0.

f(x)

касательная, параллельная оси абсцисс

х₀ х

Th. (теорема Ролля)

Пусть f: ER, которая обладает 3-мя свойствами

1. f  C[a, b]

2. f  D₁(a, b)

3. f(a) = f(b)

Тогда  с  (a, b): f’(c) = 0

В силу 1) по теореме Вейерштрасса  x₁, x₂ [a. b], в которых f(x) принимает соответственно минимальное и максимальное значения.

Тогда могут быть 2 случая:

1. f(x₁) = f(x₂)  f(x) = const f’(x) = 0; c = x (a, d)

2. f(x₁) < f(x₂) и т.к. f(a) = f(b),то отсюда , что хотя бы одна из точек x₁ или x₂ будет расположена внутри [a, b], т.е. на интервале от a до b, именно эту точку мы и возьмем в качестве точки с.

В точке с все условия теоремы Ферма выполнены поэтому f’(c) = 0

f(x)

a c’ c” b х

Th. (теорема Лагранжа о конечных приращениях)

Пусть f: ER :

1. f  C[a, b]

2. f  D₁(a, b), тогда  с  (a, b) : f(b)-f(a) = f’(c)*(b-a)

 Рассмотрим вспомогательную функцию F(x) = f(x) – (f(b)-f(a))/(b - a)*(x - a)

F (x) отличается от f(x) на линейную функцию  F(x)  C[a, b], F(x)  D₁(a, b)

F(a) = f(a); F(b) = f(b) – f(b) + f(a) = f(a) F(a) = F(b)

Все условия теоремы Ролля выполнены   с  (a, b); f’(c) = 0;

0 = F’(c) = f’(c) – (f(b)- f(a))/(b - a)  f(b) – f(a) = f’(c)*(b - a) 

Найдется точка в которой касательная параллельная хорде.