§ 5. Ннтерферирующив амплитуды

Как же это может быть, что, когда переходят от (3.15) к (3.17), т. е. когда открывается больше каналов, через фильтры начинает проходить меньше атомов? Это и есть старый, глубо­кий секрет квантовой механики — интерференция амплитуд. С такого рода парадоксом мы впервые встретились в интерферен­ционном опыте, когда электроны проходили через две щели. Помните, мы тогда увидели, что временами кое-где получается меньше электронов, когда обе щели открыты, чем когда открыта одна. Численно это получается вот как. Можно написать ам­плитуду того, что атом пройдет в приборе (3.17) через Т и S' в виде суммы трех амплитуд — по одной для каждого из трех пучков в Т; эта сумма равна нулю:

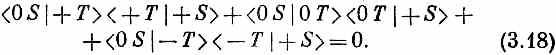
Ни одна из трех отдельных амплитуд не равна нулю: например, квадрат модуля второй амплитуды есть  [см. (3.15)], но их сумма есть нуль. Тот же ответ получился бы, если бы мы настро­или S’ на то, чтобы отбирать состояние (-S). Однако при рас­положении (3.16) ответ уже другой. Если обозначить амплитуду прохождения через Т и S' буквой а, то в этом случае мы будем иметь

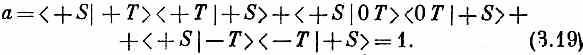
В опыте (3.16) пучок сперва расщеплялся, а потом восста­навливался. Как мы видим, Шалтая-Болтая удалось собрать обратно. Информация о первоначальном состоянии (+ S) со­хранилась — все выглядит так, как если бы прибора Т вовсе не было. И это будет верно, что бы ни поставили за «до отказа раскрытым» прибором Т. Можно поставить за ним фильтр R — под каким-нибудь необычным углом — или что-угодно. Ответ будет всегда одинаков, как будто атомы шли в S' прямо из пер­вого фильтра S.

Итак, мы пришли к важному принципу: фильтр Т или любой другой с открытыми до отказа заслонками не приводит ни к каким изменениям. Надо только упомянуть одно добавочное условие. Открытый фильтр должен не только пропускать все три пучка, но и не вызывать в них неодинаковых возмущений. Например, в нем не должно быть сильного электрического поля близ одного из пучков, которого не было бы возле других. Причина заключается вот в чем: хотя это добавочное возмуще­ние может и не помешать всем атомам пройти сквозь фильтр, оно может привести к изменению фаз некоторых амплитуд. Тогда интерференция стала бы не такой, как была, и амплитуды (3.18) и (3.19) стали бы другими. Мы всегда будем предполагать, что таких добавочных возмущений нет.

Перепишем (3.18) и (3.19) в улучшенных обозначениях. Пусть i обозначает любое из трех состояний (+Т), (0Т) и (-Т); тогда уравнения можно написать так:

и

Точно так же в опыте, в котором S' заменяется совершенно произвольным фильтром R, мы имеем

S Т R Результаты будут всегда такими же, как если бы прибор Т убрали и осталось бы только

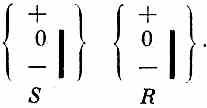
Или на математическом языке

Это и есть наш основной закон, и он справедлив всегда, если только i обозначает три базисных состояния любого фильтра. Заметьте, что в опыте (3.22) никакой особой связи между S, R и Т не было. Более того, рассуждения остались бы теми же независимо от того, какие состояния эти фильтры отбирают. Чтобы написать уравнение в общем виде без ссылок на какие-то особые состояния, отбираемые приборами S и R, обозначим через  состояние, приготовляемое первым прибором (в нашем частном примере +S), и через  — состояние, подвергаемое испытанию в конечном фильтре (в нашем примере +R). Тогда мы можем сформулировать наш основной закон (3.23) так:

где i должно пробегать по всем трем базисным состояниям некоторого определенного фильтра.

Хочется опять подчеркнуть, что мы понимаем под базисными состояниями. Они напоминают тройку состояний, которые мож­но отобрать с помощью одного из наших приборов Штерна — Герлаха. Одно условие состоит в том, что если у вас есть ба­зисное состояние, то будущее не зависит от прошлого. Другое условие — что если у вас есть полная совокупность базисных состояний, то формула (3.24) справедлива для любой сово­купности начальных и конечных состояний  и . Но не сущест­вует никакой особой совокупности базисных состояний. Мы на­чали с рассмотрения базисных состояний по отношению к при­бору Т. В равной мере мы бы могли рассмотреть другую совокуп­ность базисных состояний — по отношению к прибору S, к прибору R и т. д. Мы обычно говорим о базисных состояниях «в каком-то представлении».

Другое требование к совокупности базисных состояний (в том или ином частном представлении) заключается в том, что им положено полностью отличаться друг от друга. Под этим мы понимаем, что если имеется состояние (+T), то для него нет амплитуды перейти в состояние (О Т) или (-Т). Если i и j обозначают два базисных состояния в некотором представлении, то общие правила, которые мы обсуждали в связи с (3.8), го­ворят, что

<j|i>=0

для любых неравных между собой i и j. Конечно, мы знаем, что

<i|i>=1.

Эти два уравнения обычно пишут так:

где _ij («символ Кронекера») — символ, равный по определению нулю при ij и единице при i=j.

• Уравнение (3.25) не независимо от остальных законов, о кото­рых мы упоминали. Бывает, что нас не особенно интересует математическая задача поиска наименьшей совокупности неза­висимых аксиом, из которых все законы проистекут как след­ствия. Нам вполне достаточно обладать совокупностью, кото­рая полна и по виду непротиворечива. Однако мы беремся пока­зать, что (3.25) и (3.24) не независимы. Пусть  в (3.24) пред­ставляет одно из базисных состояний той же совокупности, что и i, скажем j-e состояние; тогда мы имеем

Но (3.25) утверждает, что <i|j> равно нулю, если только i не равно j, так что сумма обращается просто в <|j} и полу­чается тождество, что говорит о том, что эти два закона не не­зависимы.

Можно видеть, что если справедливы оба уравнения (3.25) и (3.24), то между амплитудами должно существовать еще одно соотношение. Уравнение (3.10) имело вид

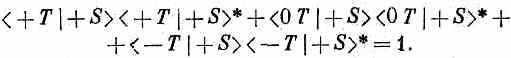
Если теперь посмотреть на (3.24) и предположить, что и , и  — это состояние (+S), то слева получится <+S|+S>, а это, конечно, равно единице, и мы должны получить (3.19)

Эти два уравнения согласуются друг с другом (для всех относи­тельных ориентации приборов Т и S) только тогда, когда

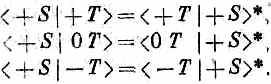
Стало быть, для любых состояний  и 

Если бы этого не было, вероятности «не сохранились бы» и частицы «терялись бы».

Прежде чем идти дальше, соберем все три общих закона для амплитуд, т. е. (3.24) —(3.26):

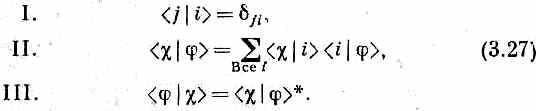
В этих уравнениях i и j относятся ко всем базисным состояниям какого-то одного представления, тогда как  и  — это любое возможное состояние атома. Важно отметить, что закон II справедлив лишь тогда, когда суммирование проводится по всем базисным состояниям системы (в нашем случае по трем: +Т, 0Т, -Т). Эти законы ничего не говорят о том, что сле­дует избирать в качестве базиса. Мы начали с прибора Т, ко­торый является опытом Штерна — Герлаха с какой-то произ­вольной ориентацией, но и всякая другая ориентация, скажем W, тоже подошла бы. Вместо i и j нам пришлось бы ставить другую совокупность базисных состояний, но все законы оста­лись бы правильными; какой-то единственной совокупности не существует. Успех в квантовой механике часто определяется тем, умеете ли вы использовать тот факт, помня, что расчет можно вести из-за этого разными путями.