Итоговая таблица с оптимальным решением

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5
x1	28/5	1	7/5	3/5	0	0
x2	12/5	0	3/5	3/5	0	1
x4	1/5	0	-1/5	1/5	1	0
	-11/5	0	-4/5	-1/5	0	0

Строка с не имеет положительных оценок с_j в последней 5-й строке. Следовательно, достигнуто оптимальное решение , которое соответствует .

Для сведения задачи на max к задаче на min надо целевую функцию умножить на (-1), а далее все рассуждения и преобразования остаются прежними. Полученное оптимальное значение опять-таки умножается на (-1), что является max значением целевой функции.

3.2.3. Метод искусственного базиса (м-метод)

В тех случаях, когда затруднительно найти первоначальный опорный план ЗЛП, т.е. выделить допустимый базис, используется искусственный базис. Метод решения при помощи искусственного базиса называется М-методом, который базируется на следующем утверждении.

Теорема. Если в оптимальном решении М-задачи все искусственные переменные равны нулю, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи. Если же в оптимальном решении одна из искусственных переменных не равна нулю или оптимальное решение отсутствует, то М-задача соответственно несовместна или неразрешима. Покажем суть метода на примере.

Пример 3.6.

min = -2x₁ + x₂ – x₃,

Приведём задачу к каноническому виду, введя новые переменные х4 и х5:

min = -2x₁ + x₂ – x₃,

Из переменных х₁ – х₅ в базис выводится только х₄, а при выводе других переменных значения свободных членов b становятся отрицательными, что недопустимо. Тогда для первого и третьего уравнений введём искусственные переменные y₁ и y₂. Новая целевая функция Т будет иметь вид

min T = + M(y₁ + y₂) = -2x₁ + x₂ – x₃ + My₁ + My₂,

где М – достаточно большое положительное число, а система ограничений с учетом y₁ и y₂ запишется как:

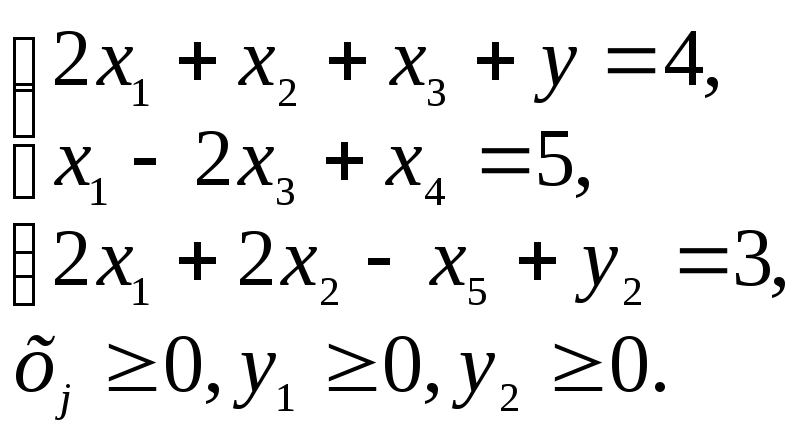
Заполним ячейки исходной симплекс-таблицы (таблица 3.5), где в качестве базисных переменных принимаются у₁, х₄ и у₂.

Таблица 3.5

Исходная таблица для решения задачи м-методом

1	2	3		4		5		6		7		8		9		10
		0		-2		1		-1		0		0		М		М
коэф. в	Базисные переменные	Свободные члены		х1		х2		х3		х4		х5		у1		у2
М	у1	4		2		1		1		0		0		1		0
О	х4	5		1		0		-2		1		0		0		0
М	у2	3	1/5	2	1	2	1	0	0	0	0	-1	-1/2	0	0	1	1/2
	Т	7М		4М+2		3М-1		М+1		0		-М		0		0

Ячейки последней строки с Т заполняем по следующим правилам:

1. Значение ячейки столбца свободных членов (3-й столбец) равно сумме произведений значений 1-го столбца (коэффициенты при базисных переменных в целевой функции Т) на соответствующие значения 3-го столбца плюс значение свободного члена целевой функции, т.е.

.

2. Значение ячейки столбца переменных х₁х₅ и у₁, у₂ равно сумме произведений значений 1-го столбца на соответствующие значения столбца переменной минус значение коэффициента при этой переменной в целевой функции, например, для 4-го столбца с х₁ имеем

и т.д.

После заполнения всех ячеек таблицы 3.5 выполняются действия как в обычном табличном симплекс-методе: выбирается разрешающий столбец, разрешающая строка и т.д. Получаем таблицу 3.6, где искусственная переменная у₂ в базисе заменяется на новую базисную переменную х₁.

Таблица 3.6