3. Методы получения оптимальных решений злп

3.1. Графический метод решения злп

3.1.1. Алгоритм решения графическим методом

З

X

ЛП имеет решение, если область определения D является выпуклым множеством точек. Множество M называется выпуклым, если X₁, X₂ M → X M.

а) б)

Рис. 3.1. Выпуклое (а) и невыпуклое (б) множества

Для выпуклых множеств, справедливо утверждение, что пересечение выпуклых множеств есть выпуклое множество. Если X₁ (x₁¹, x₂¹), X₂ (x₁², x₂²), то для выпуклого множества справедливо:

Установлено, что выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек. В теории линейного программирования доказывается, что оптимальный план, если он существует, соответствует координатам одной из угловых точек выпуклой области определения D.

Исходя из этого, и учитывая, что любая полуплоскость есть выпуклое множество, алгоритм графического метода решения ЗЛП для двух переменных x₁ и х₂ состоит в следующем:

1. Записывается ЗЛП для двух переменных x₁ и х₂.

(3.1)

,

(3.2)

(3.1)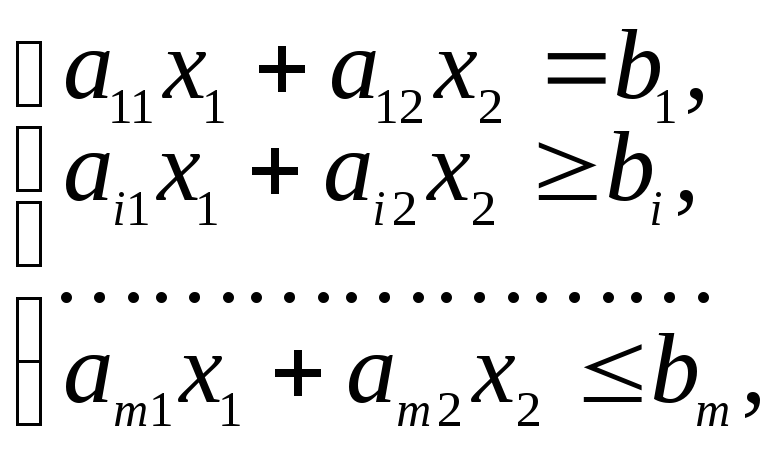

_. (3.3)

2. По ограничениям (3.2) и (3.3) строится множество всех допустимых решений D.

3. По целевой функции определяем градиент направления перемещения линии уровня = с₁ х₁ + с₂ х₂, которая перпендикулярна вектору :

4. Перемещаем линию уровня параллельно самой себе в направлении вектора . Первая точка встречи линии уровня с областью D соответствует точке min, а последняя – точке max. Если D Ø, то решений нет. Если линия уровня параллельна одной из сторон области допустимых решений D, то экстремум достигается во всех точках соответствующей стороны.

Пример. 3.1. Задача о диете и смесях.

Область ограничения представляет собой неограниченную многоугольную область. Её границы представлены уравнениями прямых:

Рис. 3.2. Графическое решение задачи о диете и смесях

Определяем

α = 4х₁ + 6х₂,

и

.

Перемещаем в направлении вектора и определяем, что точкой входа в область допустимых решений является точка В, координаты которой определяем из условия:

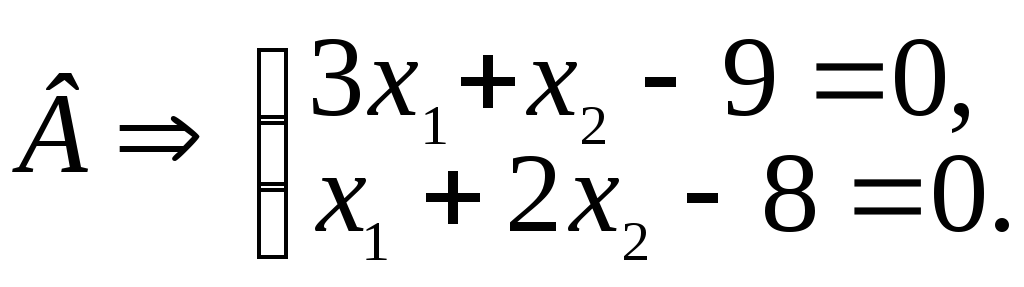
Откуда х_1В = 2; х_2В = 3

Пример 3.2. Задача об использовании ресурсов

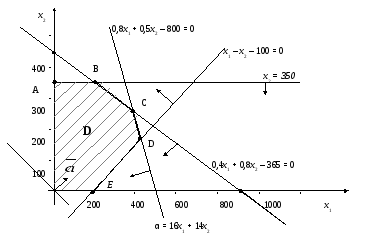
Рис. 3.3. Графическое решение задачи об использовании ресурсов

С (312,5; 300).

Пример 3.3. Задача о банке

Рис. 3.4. Графическое решение задачи о банке

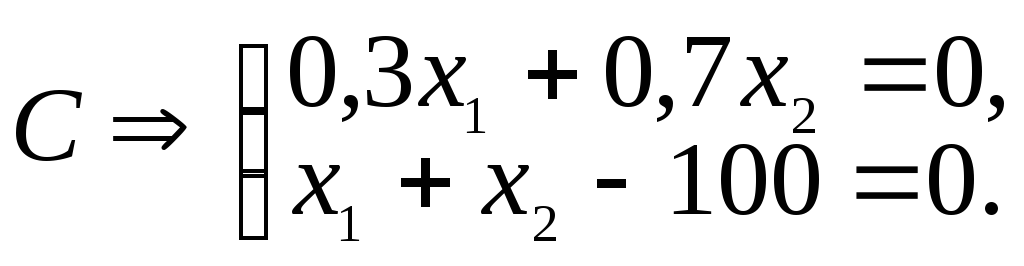
x_1c = 70; x_2c = 30.

.

Если r₁=18 %, r₂=12 %, то

3.1.2. Особые случаи решения злп графическим методом

1. max f (x₁, x₂)= 3x₁ + 5x₂,

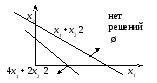
x_1,2 0.

Рис. 3.5 Случай отсутствия области решений D

2) max f (x₁, x₂)= 3x₁ + 2x₂,

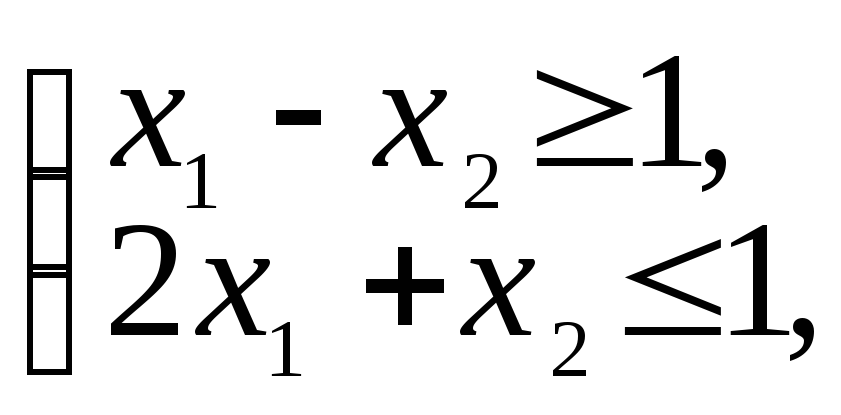
x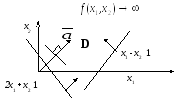_1,2 0.

Рис. 3.6 Значение целевой функции не ограниченно возрастает

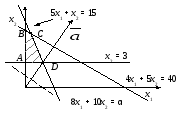
3) max f (x₁, x₂)= 8x₁ + 10x₂,

x₁ 0.

Рис. 3.7. Случай неединственности оптимального решения

Неединственность решения: множество точек отрезка ВС (ВС׀׀α).