1. Аксиомы предложений: всякая формула  языка L, которая может быт получена из некоторой тавтологии исчисления высказываний K (описанного в разд. 3 с помощью аксиом К1 – К10) в результате подстановки формул языка L на место высказывательных символов, есть логическая аксиома языка L. Всякая такая формула называется тавтологией языка первого порядка L.

2. Аксиомы кванторов

• если  и  – формулы языка L, то имеют место следующие аксиомы:

(x (  ))  (  x ), если х не входит свободно в ;

(x (  ))  (( x )  ), если х не входит свободно в ;

• для каждой формулы (х) и терма t, свободного для x, имеют место кванторные аксиомы:

 х (х)  (t);

(t)   х (х).

3. Аксиомы равенства

t = t для любого терма t;

(t = s) & (t)  (s), для любых формул (х) и термов s, t, для которых х свободна в , а s и t свободны для х (здесь (t) означает формулу (x/t)).

Правила вывода

(MP) Из формул  и    выводится  (Modus Ponens).

(Gen) Из формулы  выводится  x  (правило обобщения).

Таким образом, определена формальная теория, (разд.3.4), в которой есть формулы, аксиомы и правила вывода. Эта теория называется исчислением предикатов L.

Запись:   означает, что существует вывод формулы  из логических аксиом и формул из множества . Если  , то  – теорема исчисления предикатов L. Множество  называется противоречивым, если для каждой формулы  языка L существует вывод:  . В противном случае  называется непротиворечивым. Предложение  называется непротиворечивым, если множество {} непротиворечиво. Множество формул  называется максимально непротиворечивым, если оно не является собственным подмножеством некоторого непротиворечивого множества.

Легко доказать следующие свойства непротиворечивых множеств:

1) Множество  непротиворечиво, если и только если каждое его конечное подмножество непротиворечиво.

2) Пусть  – предложение. Тогда множество   {} противоречиво, если и только если  .

3) Пусть  – максимально непротиворечивое множество. Тогда для любых предложений  и  имеет место:

1.  , если и только если   ;

2.   , если и только если   ;

3. ( & )  , если и только если    и   ;

4) Каждое непротиворечивое множество предложений содержится в некотором максимальном непротиворечивом множестве предложений.

Теорема (о непротиворечивости исчисления предикатов). Нет формул  исчисления предикатов L, для которых существуют выводы:  и .

Доказательство. Каждой формуле  поставим в соответствие формулу h() исчисления высказываний K, множество символов P которого состоит из предикатов RL. Формулу h() определим по индукции:

1. для атомных формул;

2. , ,

,

, для любых формул ;

3. h(x) = h(), h(x) = h().

Для всякой логической аксиомы  формула h() будет тавтологией в K. Если бы для некоторой формулы  существовали выводы  и , то формулы h() и h() были бы тавтологиями в исчислении высказываний. Поскольку исчисление высказываний непротиворечиво, это невозможно. Стало быть, нет формул , для которых существуют выводы:  и .

4.3. Семантика языка логики предикатов

Моделью А языка L первого порядка называется пара, состоящая из множества А, называемого универсумом, и функции , сопоставляющей

• каждому символу константы c  L некоторый элемент ;

• каждому символу n-арной операции f из L функцию ;

• каждому предикатному символу R из L отношение .

Символ «=» интерпретируется как логический символ, такой, что .

Пример 1

Пусть L = {R} состоит из одного предикатного символа, и пусть #(R) = 2. Модель языка L задаётся как пара A = (A, ), состоящая из множества А и отношения , равного . Такую модель можно представить как ориентированный граф, вершинами которого являются элементы из А, а рёбрами – пары (a, b)  . Произвольное множество с отношением порядка будет моделью этого языка, если положить .

Пример 2

Полугруппой называется множество А вместе с бинарной операцией , удовлетворяющей закону ассоциативности a(bc) = (ab)c, для всех a, b, c  A. Полугруппа вместе с элементом e  A, удовлетворяющим для всех a  A соотношениям ea = ae = a, называется моноидом. Моноид, в котором для каждого a  A задан такой элемент , что , называется группой. Язык теории полугрупп L = {} состоит из одного элемента, #() = 2. Язык теории моноидов состоит из символов бинарной операции и константы. Язык теории групп состоит из символов бинарной и унарной операций и из символа константы. Множество действительных чисел R вместе с аддитивными операциями (R, +, -x, 0) будет моделью языка теории групп. Символы интерпретируются следующим образом:

.

Моделью языка теории групп будет также множество положительных действительных чисел с мультипликативными операциями ). Множество натуральных чисел  можно рассматривать как линейно упорядоченный моноид, если определить язык теории линейно упорядоченных моноидов как L = {+, 0, }.

Модели языка теории групп могут не удовлетворять закону ассоциативности и другим формулам, определяющим группу. Наша задача – дать формальное определение истинности предложений  в модели А языка первого порядка. Будем записывать выполнение формулы  в модели А, как А |= . Например:

(R, +, 0) |= x y (xy = e)

будет верно, поскольку для каждого a  R существует такой b  R, что a + b = 0.

Обычно не для всякого элемента модели существует символ константы, обозначающий этот элемент. Предположим, однако, что для каждого a  A существует такой символ константы в языке L, что . Интерпретацию операций можно расширить на термы, не содержащие переменных, с помощью преобразования:

.

Каждому терму t без переменных будет соответствовать элемент . Определим отношение |= («удовлетворяет формуле») по индукции:

1. A |= R , если

2. A |= , если и только если утверждение A |=  ложно;

3. A |= (  ), если и только если A |=  или A |= ;

4. A |=  x (x), если и только если существует такой b  A, что A |=  ().

Определим теперь A |=  для произвольных языка L и модели А этого языка. Пусть , где – символы констант. Обозначим через модель языка , полученную из модели A сопоставлением каждому элемента a.

Заметим, что поскольку  x (x) равносильно  x ((x)), то A |= x(x) тогда и только тогда, когда для всех b  A верно A |=  ().

Если  – предложение языка L, то положим: A |= , если и только если |= .

Пример 3

Пусть L = {, e, R} – язык теории частично упорядоченных моноидов. Рассмотрим модель N = (, +, 0, ). Справедливость утверждения:

(, +, 0, ) |=

равносильна выполнению стоящего в правой части равенства предложения для модели языка . Предложение означает, что для любых p, q, r   верно , интерпретируемое как .

Замечание. Альфред Тарский был первым, ясно осознавшим необходимость определения истинности предложения для модели. Он предложил следующий метод, отличный от рассматриваемого нами.

Пусть А – модель языка первого порядка L. Рассмотрим произвольную функцию . Будем называть её А-оценкой и представлять в виде бесконечной последовательности , i-й член которой является значением переменной , даваемой оценкой . Определяется оценка (t) для каждого терма:

1. если t есть переменная , то ;

2. если t есть константа с, то ;

3. если t есть n­-арная операция, то .

Выполнение формулы  в модели А при оценке  записывается как A |= [] и определяется по индукции:

1. A |= , если и только если ();

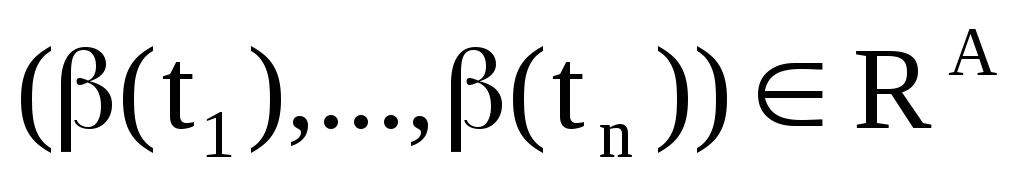2. A |=  [], если и только если A |= [] ложно;

3. A |= (  )[], если и только если A |= [] или A |= [].

4. A |=  ()[], если и только если  выполнена хотя бы на одной последовательности , отличной от  не более чем в одной i-й компоненте

Наконец, модель А называется удовлетворяющей формуле , если A |= [] для всякой оценки .

Возвращаясь к нашему первоначальному определению, отметим следующее утверждение, доказательство которого ясное, но громоздкое:

Пусть – языки первого порядка. Для любой модели А языка обозначим через множество А, рассматриваемое как модель языка . Тогда для любого предложения  языка утверждение A |=  истинно, если и только если |= .