
- •Тема 1: комплексные числа
- •Тема 2: векторы. Координаты на плоскости
- •Тема 3: прямая на плоскости. Прямая и плоскость в пространстве
- •Тема 4: матрицы и определители
- •Тема 5: системы линейных уравнений
- •Тема 6: область определения функции. Предел последовательности. Предел функции
- •Тема 7: производная функции. Дифференциал. Производные и дифференциалы высших порядков
- •Тема 8: неопределенный и определенный интегралы
- •Тема 9: ряды
- •Тема 10: функции нескольких переменных
- •Тема 11: дифференциальные уравнения
- •Тема 12: основы теории вероятностей
Тема 3: прямая на плоскости. Прямая и плоскость в пространстве
-
Укажите уравнение прямой, проходящей через точки C(0; 1) и D(– 2; 0). а) 2у – x – 2 = 0;
б) 5х – 3у + 3 = 0;
в) у – 2х = 0;
г) 3х + у + 6 = 0.
-
Укажите уравнение прямой, проходящей через точку А(1; 1) и имеющую угловой коэффициент k = 1. а) у = 1 – х;
б) у = х;
в) у = х+2;
г) у = 2х – 1.
-
Укажите уравнение прямой, проходящей через точку А(3; – 2) и имеющую угловой коэффициент k = – 1. а) у = х;
б)
![]() ;
;
в) у = x – 5;
г) у = 1 – х.
-
Укажите прямую, параллельную прямой 2х + 3у – 7 = 0. а) 3х + 2у – 7 = 0;
б) x + 3у – 2 = 0;
в) 2х – у – 7 = 0;
г) 2х + 3у + 9 = 0.
-
Укажите прямую, не параллельную прямой у = 2х + 3. а) 4у = 8х + 1;
б) у = 2х – 4;
в) 2у = 4х – 5;
г) у = 3х – 3.
-
Укажите прямую, перпендикулярную прямой 3х – у – 3 = 0. а) x + 3у – 17 = 0;
б) 2х – у + 4 = 0;
в) x – 3у + 2 = 0;
г) x + у = 0.
-
Укажите прямую, не перпендикулярную прямой 2х + 5у – 6 = 0. а) 5х – 2у + 3 = 0;
б) 5х + 2у – 1 = 0;
в) 10х – 4у – 7=0;
г) 15х – 6у + 11 = 0.
-
Укажите точку, лежащую на прямой у = 8х – 6. а) (1; 3);
б) (0; 6);
в) (– 1; – 14);
г) (2; 9).
-
Укажите точку, не лежащую на прямой у =
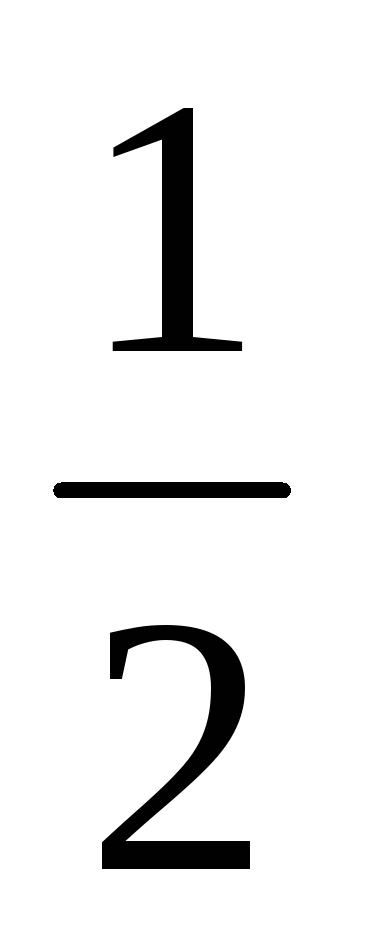 x
+ 4.
а) (0; 4);
x
+ 4.
а) (0; 4);
б) (2; 6);
в) (– 4; 2);
г) (– 8; 0).
-
Найдите координаты точки пересечения прямой 4х – 3у – 10 = 0 с осью абсцисс. а)
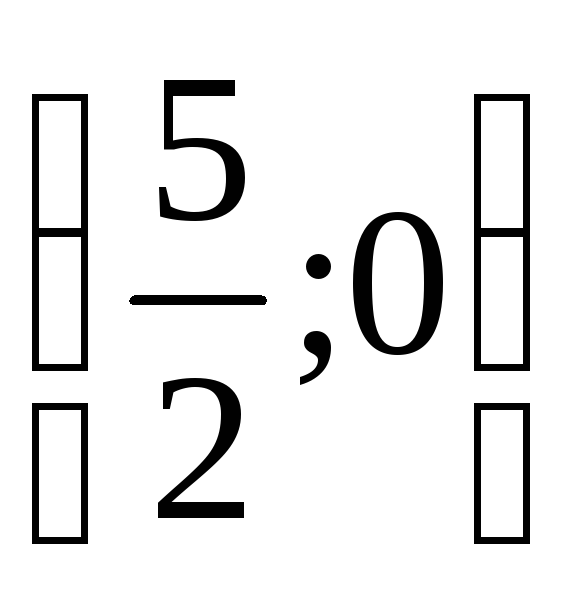 ;
;
б)
![]() ;
;
в) (0; 0);
г) (– 2; 0).
-
Найдите координаты точки, пересечения прямой 2х + 3у – 4 = 0 с осью ординат. а) (2; 0);
б)
![]() ;
;
в) (0; 0);
г) (– 1; 2).
-
Найдите координаты точки пересечения прямых у = 6х – 5 и у = x + 7. а) (0;– 5);
б) (1; 1);
в) ( 2,4; 9,4);
г) ( 1,5; 4).
-
Укажите уравнение прямой, проходящей через точку А(2; 3) и параллельной прямой у = 2х + 5. а) у = x + 1;
б) у = 2х – 3;
в) у = 3х + 2;
г) у = 2х – 1.
-
Укажите уравнение прямой, проходящей через точку В(– 1; 5) и параллельной прямой у = 7х – 1. а) у = 7х + 12;
б) у = 4 –x;
в) у = 3х + 8;
г) у = 7х + 4.
-
Укажите уравнение прямой, проходящей через точку В(– 3; 2) и перпендикулярной прямой 7х + 4у – 11 = 0. а) 2х – 3у + 12=0;
б) 4х – 7у + 26 = 0;
в) 4х – 7у + 11 = 0;
г) 2у – 3х = 0.
-
Укажите уравнение прямой, проходящей через точку В(– 1, 4) и перпендикулярной прямой 5х – 3у + 4 = 0. а) 5х – 3у + 17 = 0;
б) у – 4х = 0;
в) 3х + 5у – 17 = 0;
г) 3х + 5у + 2 = 0.
-
Прямая задана уравнением 2х – 4у + 3 = 0. Укажите координаты нормального вектора этой прямой. а) (2; 3); б) (2; 4); в) (4; 3); г) (2; – 4).
-
Прямая задана уравнением – 2х +5у –8 = 0. Укажите координаты нормального вектора этой прямой. а) (– 2; 5); б) (5; – 8); в) (– 5; – 2); г) (5; – 8).
-
Прямая задана уравнением – 3х +8у – 1 = 0. Укажите координаты направляющего вектора этой прямой. а) (– 3; 8); б) (– 8; – 3); в) (3; – 8); г) (– 3; – 1).
-
Прямая задана уравнением 5х +6у – 2 = 0. Укажите координаты направляющего вектора этой прямой. а) (5; – 6); б) (5; 6); в) (– 6; 5); г) (2; – 6).
-
Найдите расстояние от точки М(– 6; 3) до прямой 3х – 4у + 15 = 0. а) 3;
б) 4;
в) 5;
г) 1.
-
Найдите расстояние от точки N(– 2; – 1) до прямой 12х + 5у + 3 = 0. а) 4;
б) 3;
в) 2;
г) 1.
-
Угол между прямыми x – 2у – 2 = 0 и у =
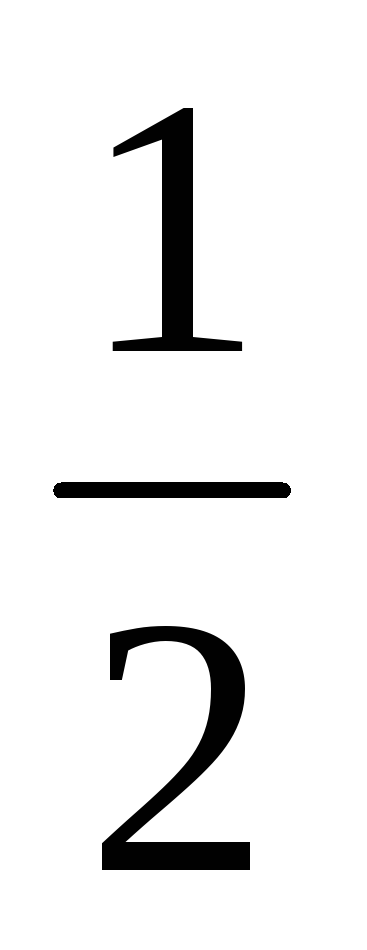 x
+ 3 равен:
а)
0;
x
+ 3 равен:
а)
0;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Уравнение прямой, проходящей через две точки А1 (х1; y1) и A2 (x2; y2) имеет вид: а)
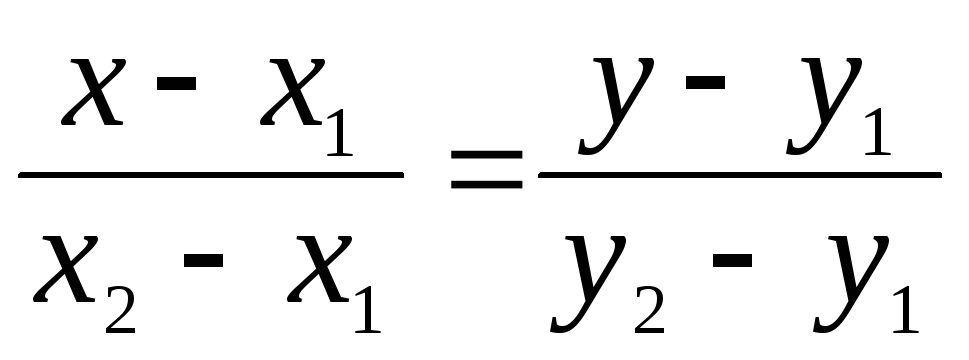 ;
б)
;
б)
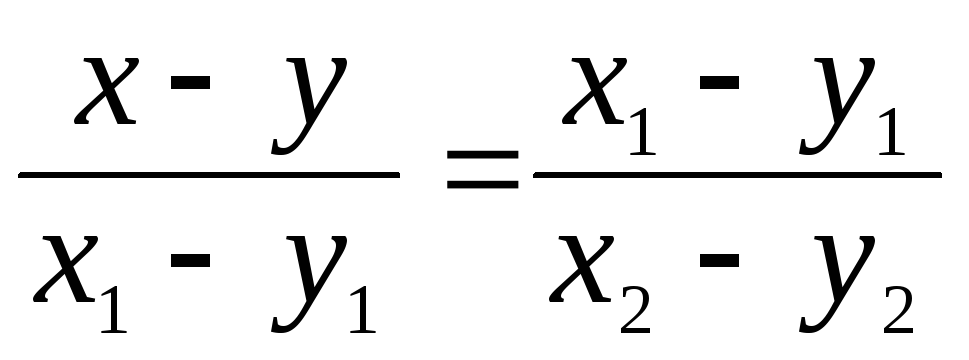 ;
в)
;
в)
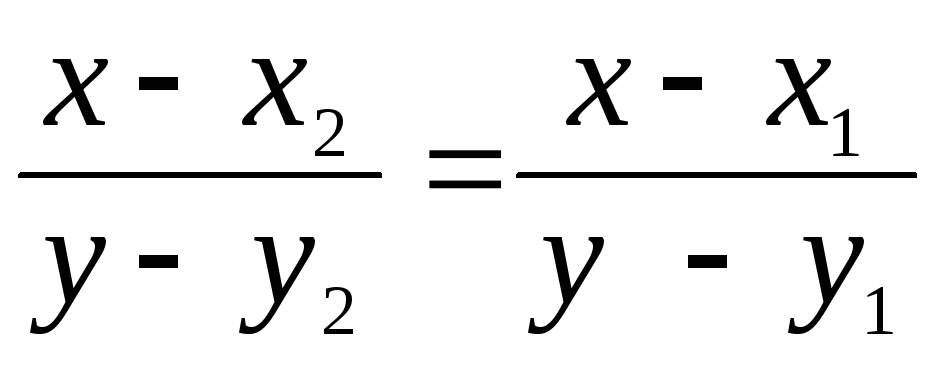 ;
г)
;
г)
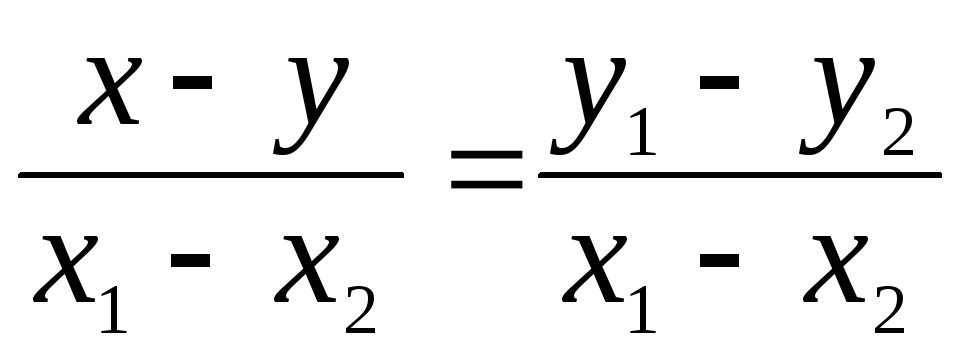 .
.
-
Уравнение прямой с направляющим вектором
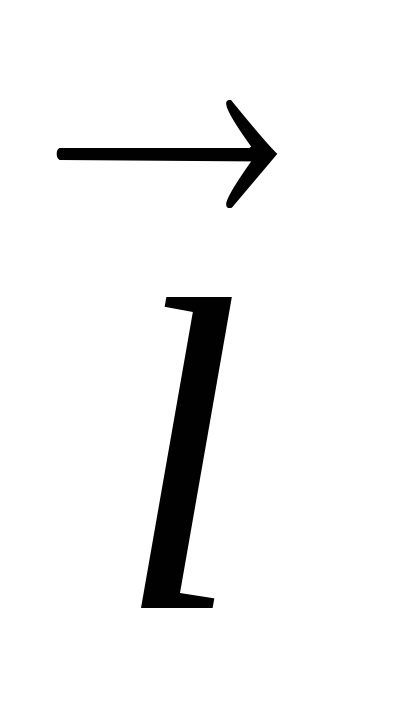 (m;
n),
проходящей через точку М
(x0;
y0)
имеет вид:
а)
(m;
n),
проходящей через точку М
(x0;
y0)
имеет вид:
а)
 ;
б)
;
б)
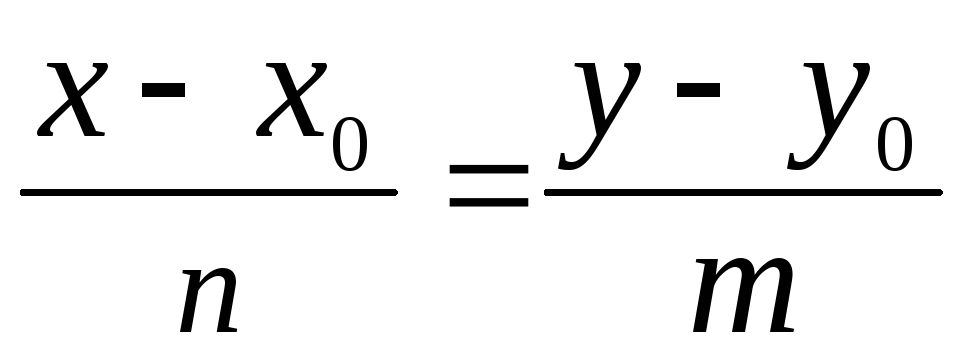 ;
в)
;
в)
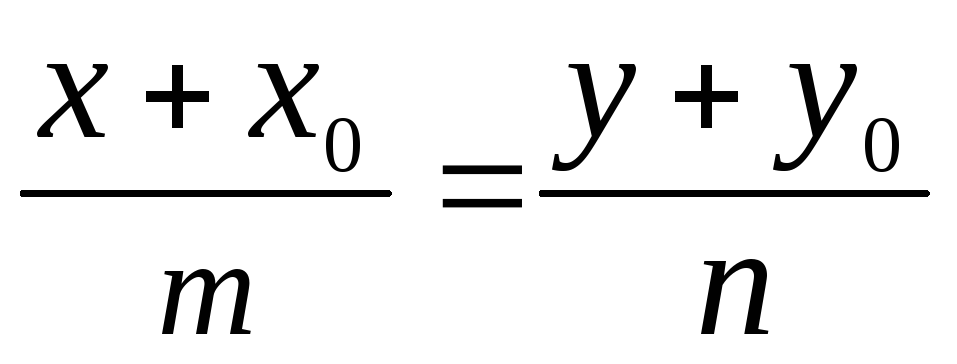 ;
г)
;
г)
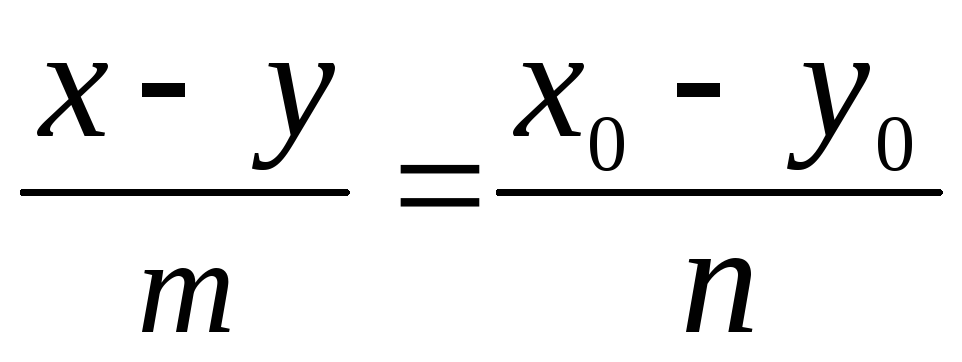 .
. -
Уравнение прямой, проходящей через данную точку М (x0; y0) с данным угловым коэффициентом k имеет вид: a) y – y0 = k (x – x0); б) y = k x + b; в) y + y0 = k (x + x0); г) y = k (x – x0) – y0.
-
Уравнение плоскости по точке М0 (x0, y0, z0) и нормальному вектору
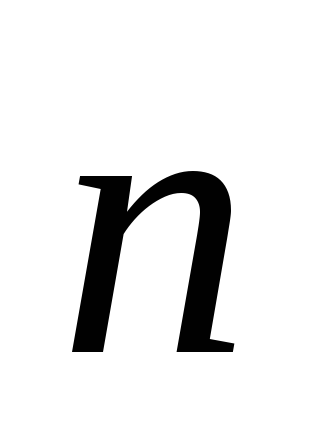 = (A,
B,
C)
записывается следующим образом:
а)
= (A,
B,
C)
записывается следующим образом:
а)
 +
+
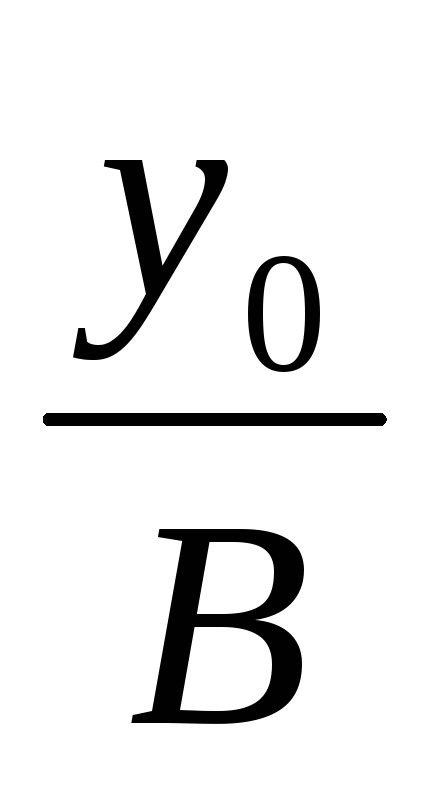 +
+
 = 1;
= 1;
б) Ax0 + By0 + Cz0 = 0;
в)
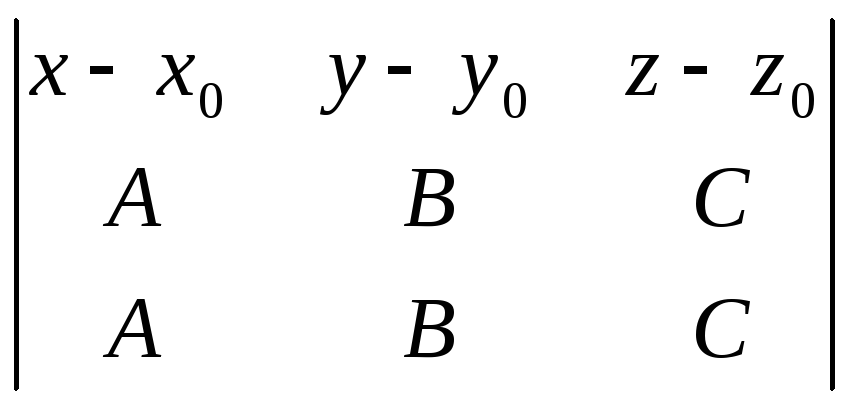 = 0;
= 0;
г) A(x – x0) + B(y – y0) + C(z – z0) = 0.
-
Уравнение плоскости «в отрезках», где a, b и c – отличные от нуля отрезки, отсекаемые плоскостью от осей координат, записывается следующим образом: а)
 +
+
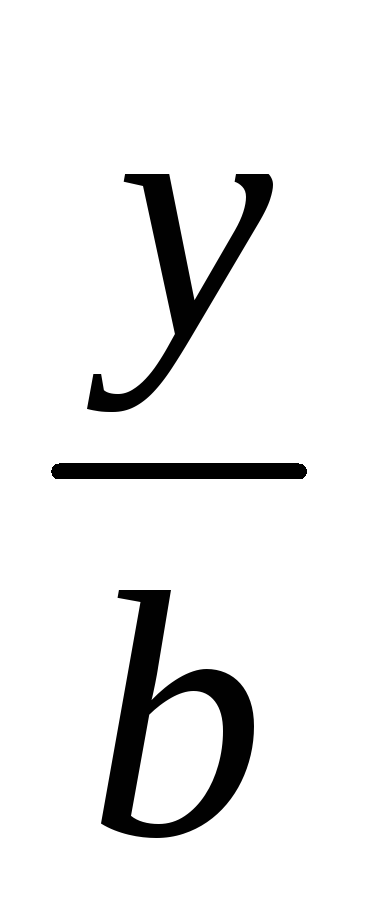 +
+
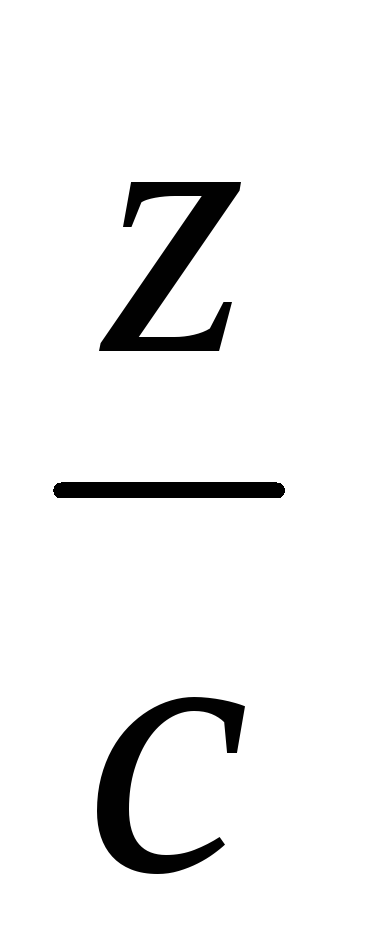 = 1;
= 1;
б) Ax + By + Cz = 0;
в)
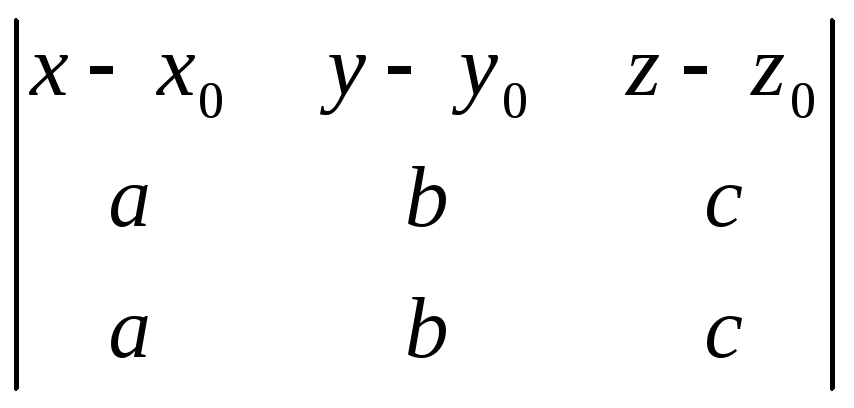 = 0;
= 0;
г)
![]() +
+
![]() +
+
![]() = 0.
= 0.
-
Уравнение плоскости по трем точкам М1 (x1, y1, z1), М2 (x2, y2, z2), М3 (x3, y3, z3) записывается следующим образом:
а) A(x – x0) + B(y – y0) + C(z – z0) = 0;
б)
![]() +
+
![]() +
+
![]() = 1;
= 1;
в)
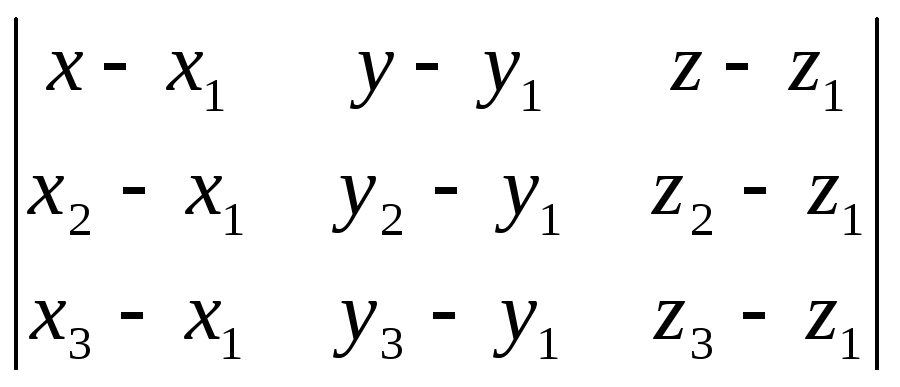 = 0;
= 0;
г) Ax + By + Cz + D = 0.
-
Укажите точку, принадлежащую плоскости 3x – 5y + 2z – 17 = 0:
а) (4; 1; 2);
б) (2; – 1; 3);
в) (7; 1; 2);
г) (0; – 4; 2).
-
Укажите точку, принадлежащую плоскости x – 3y + 4z – 5 = 0:
а) (– 2; – 1; 1);
б) (0; 3; 2);
в) (7; 1; – 1);
г) (4; 2; 2).
-
Укажите уравнение плоскости, проходящей через точку М0 (1; – 5; 6) перпендикулярно вектору
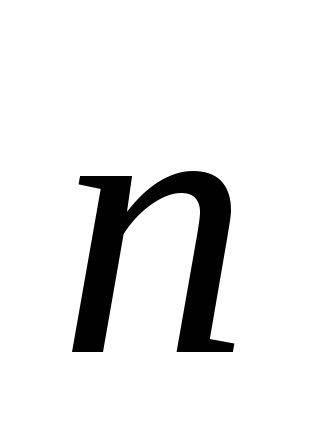 = (4; 2; – 3):
= (4; 2; – 3):
а) 5x – 3y + 3z = 0;
б) 4x + 2y – 3z + 2 = 0;
в) 4x + 2y – 3z + 24 = 0;
г) 3x + 7y – 9z = 0.
-
Укажите уравнение плоскости, проходящей через точку М0 (2; 3; 5) перпендикулярно вектору
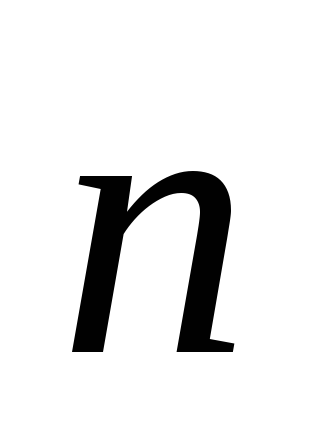 = (1; – 4; 7):
= (1; – 4; 7):
а) x – 4y + 7z + 20 = 0;
б) 2x + 3y + 5z – 24 = 0;
в) x – 4y + 7z – 25 = 0;
г) x – 4y + 7z = 0.
-
Даны точки М1(0; – 1; 3) и М2(1; 3; 5). Укажите уравнение плоскости, проходящей через точку М1 перпендикулярно вектору
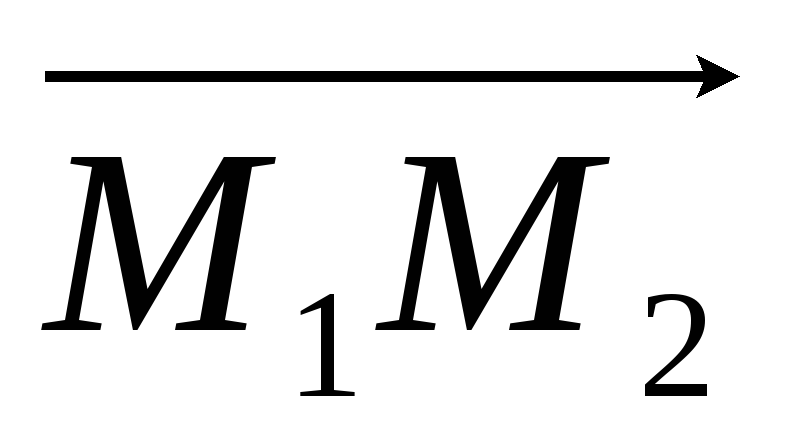 .
.
а) x + 3y + 5z + 12 = 0;
б) x + 4y + 2z – 2 = 0;
в) – y + 3z – 10 = 0;
г) x + 4y + 2z = 0.
-
Даны точки М1(4; 2; 1) и М2(6; 12; – 3). Укажите уравнение плоскости, проходящей через точку М1 перпендикулярно вектору
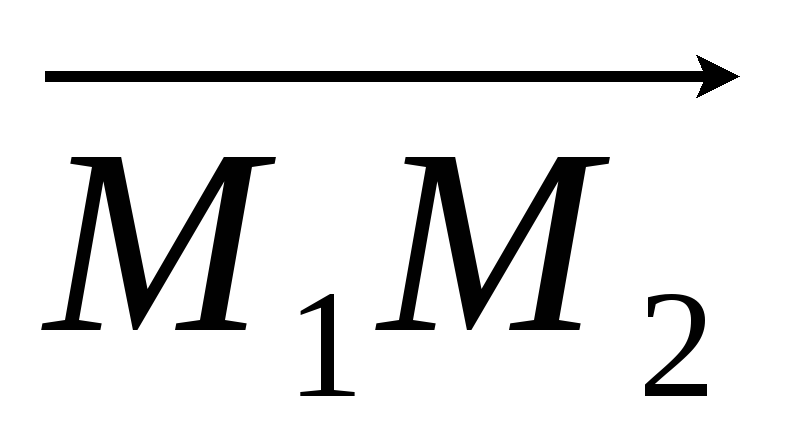 .
.
а) 2x + 10y – 4z – 24 = 0;
б) 2x + 10y – 4z = 0;
в) 4x + 2y + z = 0;
г) 6x + 12y – 3z = 0.
-
Укажите уравнение плоскости, проходящей через точки А(7; 6; 7), В(5; 10; 5) и С(– 1; 8; 9):
а) 4x + 18y + 14z = 0;
б) 6x + 2y – 4z = 0;
в) 3x + 5y + 7z = 100;
г) 6x + 12y – 3z = 25.
-
Найдите расстояние от точки А(5; 1; – 1) до плоскости x – 2y – 2z + 4 = 0:
а) 1;
б) 1,5;
в) 2;
г) 3.
-
Найдите расстояние от точки А(1; 2; 3) до плоскости 2x – 2y + z – 3 = 0:
а) 1;
б)
![]() ;
;
в)
![]() ;
;
г) 2.
-
Угол между плоскостями 2х + 3y – 2z – 4= 0 и 13x – 8у + z + 44 = 0 равен: а)
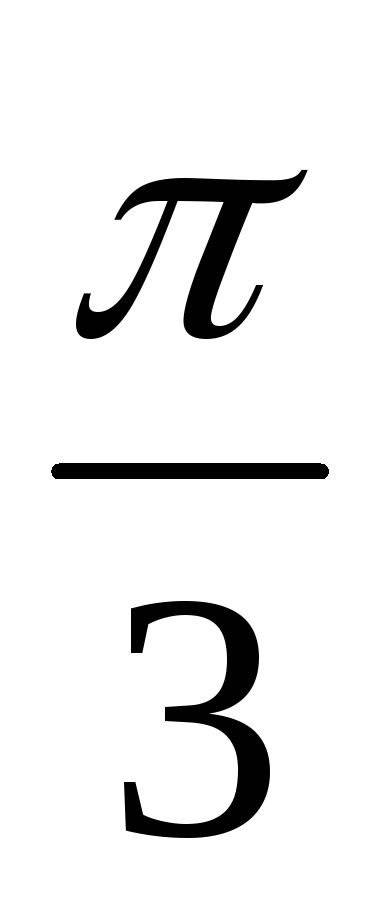 ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Угол между плоскостями 3х + 2y – 7z +8 = 0 и 3x + 2у – 7z + 32 = 0 равен: а) 60;
б) 45;
в) 30;
г) 0.
