§7.15. Електропровідність металів і напівпровідників
Відомо
(розділ 3), що густина електричного струму
в провідниках (металах, напівпровідниках,
електролітах тощо) визначається зарядом
носіїв, їх концентрацією n та середньою
швидкістю напрямленого (дрейфового)
руху
,
зумовленого електричним полем напруженістю
.
Якщо носіями струму є електрони, то
густина струму
(7.98)
В слабких електричних полях, де виконується закон Ома, швидкість напрямленого руху лінійно залежить від напруженості електричного поля, тобто
, (7.99)
де
– рухливість електронів.
Підставляючи (7.99) у (7.98), отримаємо
, (7.100)
тобто закон Ома в диференційній формі, де
(7.101)
– питома електропровідність електронного провідника (металу, напівпровідника n-типу).
Питома електропровідність власного напівпровідника
, (7.102)
де
– рухливість дірок.
Рухливість носіїв визначається так званим часом релаксації , який формально можна розглядати як проміжок часу між двома послідовними актами зіткнення (розсіяння) носіїв з недосконалостями кристалу. Основними недосконалостями (відхиленнями від ідеальності) є коливання кристалічної решітки (фонони) і домішки кристалу. В рамках вказаного формалізму середній час релаксації носіїв
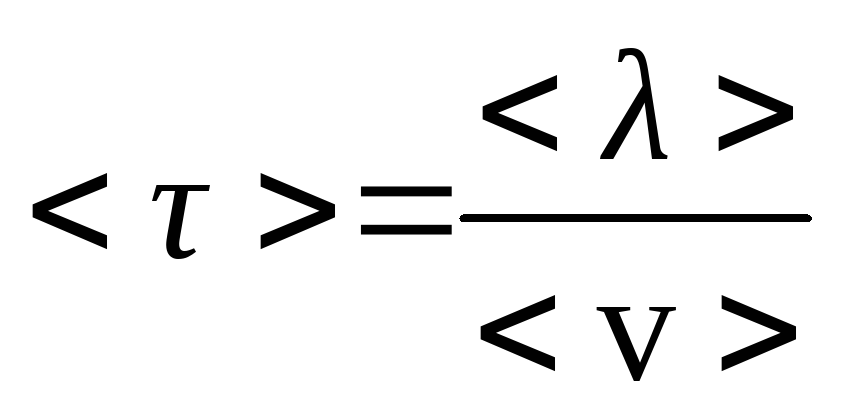, (7.103)
де
– середня довжина вільного (між двома
послідовними зіткненнями) пробігу
носіїв,
– середня швидкість теплового (хаотичного)
руху носіїв.
Строга квантова теорія дає
. (7.104)
Підставляючи (7.104) у (7.101), отримаємо для питомої електропровідності
. (7.105)
Оскільки
в металах концентрація носіїв (електронів
у c-зоні) від температури не залежить,
то залежність питомої електропровідності
визначається лише відношенням
.
Виявляється, що, за винятком дуже низьких
температур,
.
І тому
,
а питомий опір
,
у відповідності з відомим експериментальним
законом
.
Відмітимо, що при оціночних розрахунках
можна покладати
.
Принципово інша ситуація в напівпровідниках, де концентрація носіїв експоненційно залежить від температури (7.95–7.97). Рухливість носіїв в напівпровідниках також залежить від температури, але за значно слабшим, степеневим законом
,
де при різних температурах приймає значення від – 1,5 до + 1,5. Підставляючи (7.95–7.97) у (7.101; 7.102), отримаємо вирази для питомої електропровідності:
власного
(n=p)
напівпровідника
,(7.106)
домішкового
n-типу 
(7.107)
домішкового
p-типу 
, (7.108)
де
передекспоненційні множники
можемо наближено вважати від температури
незалежними. Формули (7.106 – 7.108) можна
узагальнити у вигляді
, (7.109)
де
– енергія активації провідності, яка
у власному напівпровіднику дорівнює
,
а у домішкових напівпровідниках має
зміст половини енергії іонізації донорів
чи акцепторів. Отже, питома електропровідність
напівпровідників експоненційно
збільшується з ростом температури, чим
останні принципово відрізняються від
металів.
Температурна залежність питомого опору напівпровідникового кристалу, як випливає з (7.109),
Рис.7.32
або
В
широкій області температур експериментальна
залежність
(рис. 7.32) має три ділянки: 1 – домішкової
провідності; 2 – повної іонізації домішок
(n =
[Д]
для кристалу n-типу);
3 – власної провідності.