Основные правила дифференцирования

ТЕОРЕМА 1. Если функции u = u(x) и v = v(x) дифференцируемы в точке х, то функции u + v, uv, дифференцируемы в этой точке, причем:

1) ;

2)

3) ;

4)

ТЕОРЕМА 2 (производная сложной функции). Если функция g(x) дифференцируема в точке х₀, а функция f (у) дифференцируема в точке у₀ = g(x₀), то сложная функция f (g(x)) дифференцируема в точке х₀ и

или .

Таблица основных производных

1) с' = 0, с ;

2) х' =1;

3) (хⁿ)' = nx^n-1, n ;

4) (а^х)' = а^х lnа, 0 < a  1;

5) (e^x)' = e^x;

6) 0 < a  1, х > 0;

7) х > 0;

8) (sin x)' = cos x;

9) (cos x)' = – sin x;

10) ;

11) ;

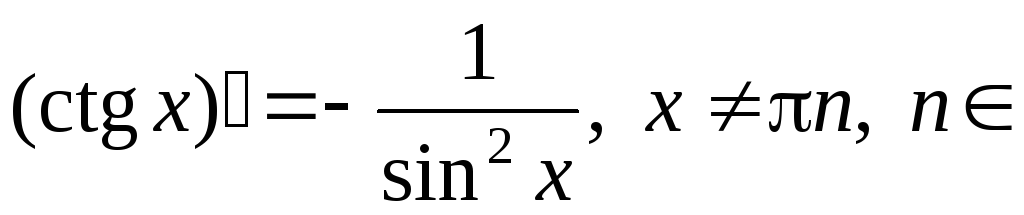12) ;

13) ;

14) ;

15) .

ПРИМЕР 3

Найти уравнения касательной и нормали к графику функции f (x) = = 3х² + 4 в точке х₀ = 2.

Решение

Найдем производную функции f (x): f'(x) = 6х.

Для того чтобы составить уравнения касательной и нормали (5) и (6), необходимо найти значения функции и ее производной в точке х₀ = 2:

f (2) = 3  2² + 4 = 16,

f ' (2) = 6  2 = 12.

Следовательно, уравнение касательной имеет вид:

у = 12 (х – 2) + 16,

уравнение нормали:

Ответ: у = 12 (х – 2) + 16,

ПРИМЕР 4

Найти производные функций.

а) ;

б) ;

в) ;

г) .

Решение

а) ;

б)

;

в) ;

г)

В примере г) мы вначале взяли производную степенной функции, затем производную sin 8x, а в конце производную 8х.

2. Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков

Логарифмическое дифференцирование применяют тогда, когда нужно найти производную выражения, содержащего произведения, корни, степени, то есть выражение, которое легко логарифмируется, а также для нахождения производной степенно-показательной функции u(x)^v(x).

ПРИМЕР 5

Найти производную функции.

а) ;

б) .

Решение

а) прологарифмируем функцию у

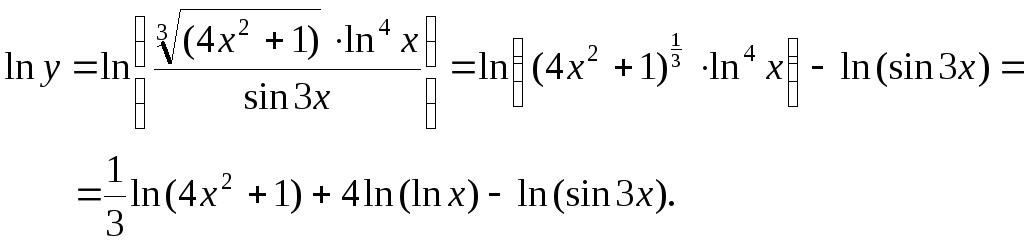
Находим производную левой и правой частей данного выражения, учитывая, что :



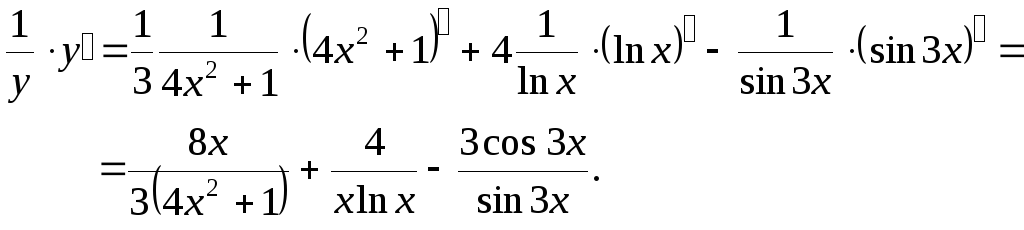
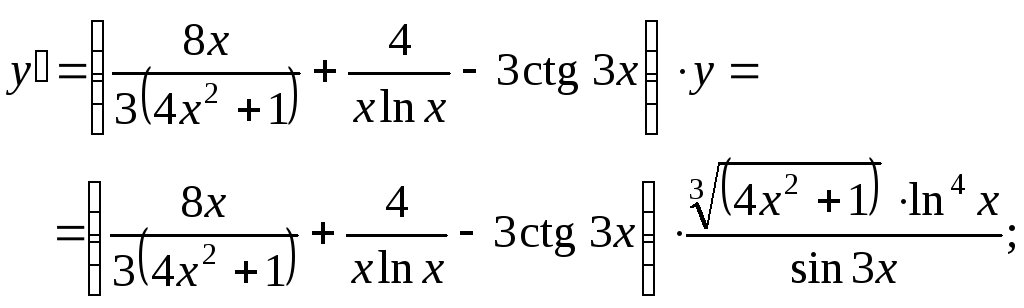
б) прологарифмируем степенно-показательную функцию . (Степенно-показательная функция – это функция, у которой функциями являются и основание и показатель степени).

Находим производную левой и правой частей данного выражения:

.

Функция называется заданной неявно, если она представлена в виде

F(x, y) = 0,

то есть «у» не выражен явно, или его, в принципе, нельзя выразить явно через х. В этом случае производная находится, учитывая, что «у» – функция. Например, .

ПРИМЕР 6

Найти производную.

Решение

Продифференцируем данное выражение



Второй производной от функции у = f (x) называется производная от ее первой производной у' = f '(x). Обозначается вторая производная следующим образом: у'', f '', Аналогично определяются производные третьего и более высоких порядков. Например, производная сотого порядка обозначается как у⁽¹⁰⁰⁾ или .

ПРИМЕР 7

Найти производные функции

Решение

у' = 20х⁴ + 4х,

у'' = 80х³ + 4,

у''' = 240х²,

у⁽⁴⁾ =

у⁽⁵⁾ = 480,

у⁽⁶⁾ = 0.

Заметим, что для степенной функции количество производных, отличных от нуля, равно наивысшей степени функции. В данном примере пять производных не равны нулю.

Лекция 2. ПРАВИЛО ЛОПИТАЛЯ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ

План

1. Раскрытие неопределенностей при помощи правила Лопиталя.

2. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.