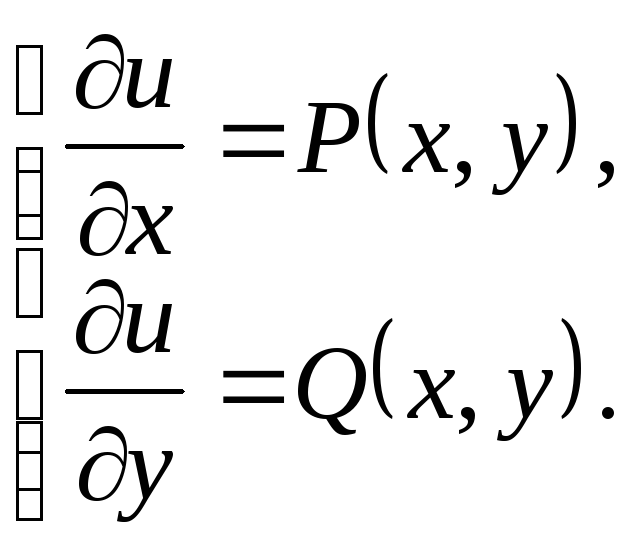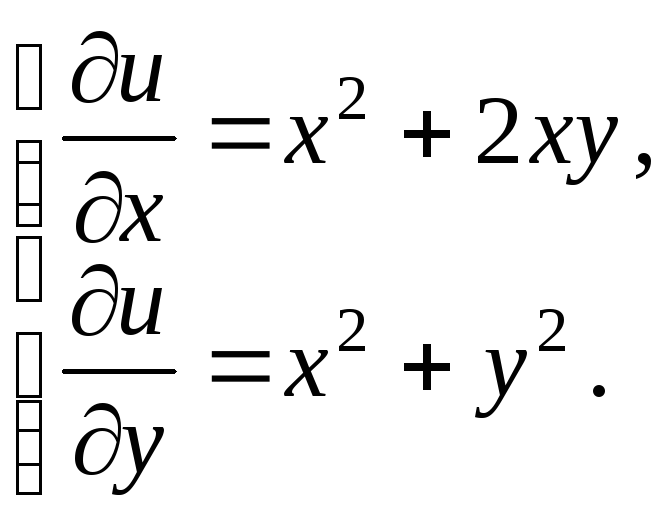- •Ю. В. Минченков высшая математика Дифференцированные уравнения
- •Ключевые понятия
- •1. Основные понятия теории дифференциальных уравнений
- •2. Дифференциальные уравнения первого порядка. Задача Коши
- •3. Дифференциальные уравнения с разделяющимися переменными
- •Ключевые понятия
- •1. Однородные дифференциальные уравнения
- •2. Линейные дифференциальные уравнения
- •1. Метод подстановки (метод Бернулли).
- •2. Метод вариации произвольной постоянной (метод Лагранжа).
- •3. Уравнения в полных дифференциалах
- •Задачи и упражнения
- •Литература
- •Содержание
- •Минченков Юрий Владимирович высшая математика Дифференциальные уравнения
- •220086, Минск, ул. Славинского, 1, корп. 3.
2. Метод вариации произвольной постоянной (метод Лагранжа).
Рассмотрим уравнение (3):
|
|
Найдем вначале общее решение однородного уравнения
![]() .
.
Его решением будет функция (11):
|
|
По методу вариации произвольной постоянной общее решение (3) ищут в виде (11), полагая в этом соотношении величину С функцией от х:
|
|
(17) |
![]()
|
|
(18) |
Подставим (17), (18) в (3):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
|
|
(19) |
Подставив
![]() из (19) в (17), получим общее решение
дифференциального уравнения (3),
совпадающее, естественно, с формулой
(10):
из (19) в (17), получим общее решение
дифференциального уравнения (3),
совпадающее, естественно, с формулой
(10):
![]() .
.
ПРИМЕР 4
Решить уравнение (12) методом вариации произвольной постоянной
|
|
Решение
Вначале рассмотрим
однородное уравнение
![]() .
Решим его:
.
Решим его:
![]() ,
,
![]() ,
,
|
|
(20) |
Функция (20) – решение однородного уравнения. Учитывая вид (20), решение неоднородного уравнения (12) будем искать в виде
|
|
(21) |
|
|
(22) |
Подставим (21), (22) в (12):
![]() ,
,
![]() ,
,
|
|
(23) |
Подставим (23) в (21). В итоге получаем решение исходного уравнения (12):
|
|
(24) |
Функция (24), естественно, совпала с функцией (16), так как эти функции являются решением одного и того же уравнения (12).
Рассмотрим следующий важный класс дифференциальных уравнений первого порядка.
Уравнением Бернулли называется уравнение вида
|
|
(25) |
где
![]() .
В случае
.
В случае
![]() ,
,
![]() уравнение (25) является линейным уравнением
(3). Во всех других случаях оно сводится
к линейному с помощью подстановки
уравнение (25) является линейным уравнением
(3). Во всех других случаях оно сводится
к линейному с помощью подстановки
|
|
(26) |
ПРИМЕР 5
Решить уравнение
|
|
(27) |
Решение
Уравнение (27) – уравнение Бернулли, так как из
![]()
|
|
(28) |
т. е.
![]() .
.
Используя подстановку
![]() ,
преобразуем уравнение Бернулли (28) в
линейное:
,
преобразуем уравнение Бернулли (28) в
линейное:
 ,
,
|
|
(29) |
Решим линейное дифференциальное уравнение (29) методом Лагранжа (вариации произвольной постоянной):
1. Вначале решим соответствующее однородное линейное уравнение:
![]() ,
,
![]() ,
,
|
|
(30) |
2. Пусть
![]() – решение (29)
– решение (29)
|
|
(31) |
Подставим
![]() и
и
![]() в (29):
в (29):
![]() ,
,
![]() ,
,
![]() ;
;
а) вычислим
![]() методом интегрирования по частям:
методом интегрирования по частям:
![]() ,
,
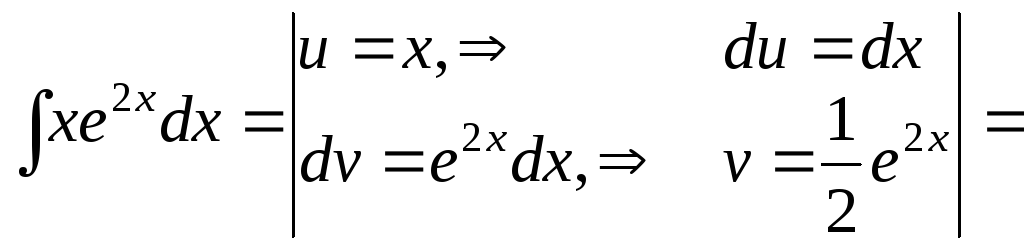
|
|
(32) |
б)
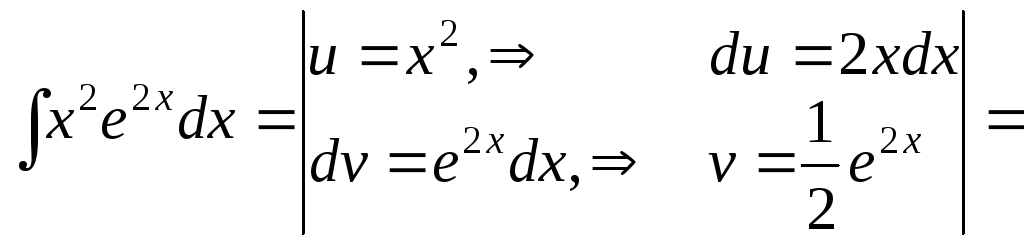
|
|
(33) |
Следовательно, используя (32), (33):
![]()
![]() .
.
Таким образом:
|
|
(34) |
Подставим (34) в
решение
![]() :
:
![]() .
.
Переходя к переменной
у
(из подстановки
![]() ),
получаем решение исходного уравнения
(27):
),
получаем решение исходного уравнения
(27):
![]() .
.
3. Уравнения в полных дифференциалах
Уравнением в полных дифференциалах называется дифференциальное уравнение первого порядка вида
|
|
(35) |
левая часть которого
есть полный дифференциал некоторой
функции
![]() .
.
Напомним, что
полным дифференциалом функции
![]() называется выражение
называется выражение
|
|
(36) |
где
![]() и
и
![]() – частные производные.
– частные производные.
Следовательно, уравнение (35) можно записать в виде
|
|
(37) |
Поэтому функция
|
|
(38) |
есть общий интеграл (решение) дифференциального уравнения (35).
Необходимым и достаточным условием того, чтобы уравнение (35) было уравнением в полных дифференциалах, является выполнение условия
|
|
(39) |
Учитывая (36), функция
![]() может быть найдена из системы уравнений:
может быть найдена из системы уравнений:
|
|
(40) |
В случае, когда не выполняется условие (39), т. е. левая часть (35) не является полным дифференциалом некоторой функции, иногда можно найти функцию М (х, у) такую, что
![]() ,
,
т. е. умножив
![]() на М
(х,
у),
уравнение становится уравнением в
полных дифференциалах. В этом случае
функция М
(х,
у)
называется интегрирующим
множителем:
на М
(х,
у),
уравнение становится уравнением в
полных дифференциалах. В этом случае
функция М
(х,
у)
называется интегрирующим
множителем:
1. Если
|
|
(41) |
то интегрирующий множитель зависит только от х, т. е. М = М (х), причем
|
|
(42) |
2. Если
![]() ,
,
то интегрирующий множитель зависит только от у, т. е. М = М (у), причем
|
|
(43) |
ПРИМЕР 6
Решить уравнение
|
|
(44) |
Решение
Уравнение (44) – это уравнение в полных дифференциалах, так как
![]() ,
,
![]() – условие (39)
выполняется.
– условие (39)
выполняется.
Заметим, что это
уравнение является также однородным
дифференциальным уравнением первого
порядка, т. е. его, в принципе, можно
решить, используя подстановку
![]() .
.
Левая часть (44)
является полным дифференциалом некоторой
функции
![]() :
:
![]() ,
,
т. е.
|
|
(45) |
Проинтегрируем
по х
первое из уравнений (45), считая у
постоянным, при этом вместо постоянной
интегрирования надо поставить
![]() :
:
|
|
(46) |
Продифференцируем эту функцию по у и учтем второе уравнение (45):
![]() .
.
Следовательно, из (46):
![]() ,
,
где
![]() – общий интеграл исходного дифференциального
уравнения.
– общий интеграл исходного дифференциального
уравнения.
ПРИМЕР 7
Проинтегрировать уравнение
|
|
(47) |
Решение
![]() ,
,
![]() .
.
Так как
![]() ,
то уравнение (47) не является уравнением
в полных дифференциалах. Попробуем
найти для него интегрирующий множитель:
,
то уравнение (47) не является уравнением
в полных дифференциалах. Попробуем
найти для него интегрирующий множитель:
![]()
![]() ,
,
т. е. выполняется условие (41). Следовательно, из (42):
![]() ,
,
|
|
(48) |
Умножим уравнение
(47) на
![]() :
:
![]() ,
,
|
|
(49) |
Уравнение (49) – уравнение в полных дифференциалах, так как
![]()
![]() т. е.
т. е.
![]() ,
,
значит, условие (39) выполнено.
Решаем (49) аналогично, как и в примере 6:
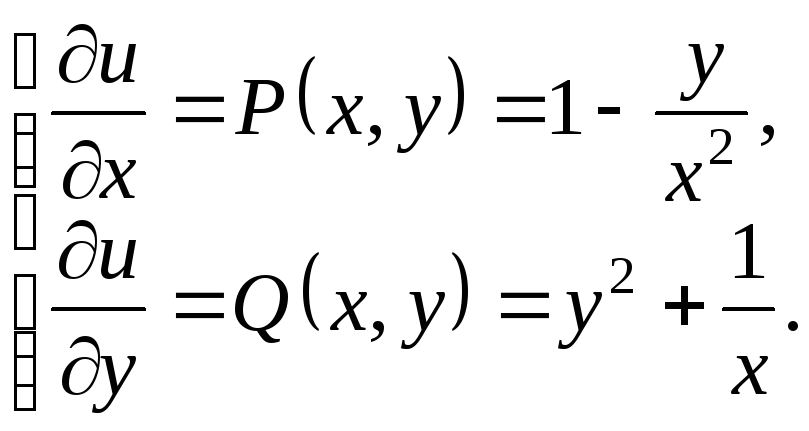
|
|
(50) |
![]() ,
,
![]() .
.
Подставим
![]() в формулу (50):
в формулу (50):
![]() .
.
Общий интеграл исходного дифференциального уравнения имеет вид:
![]() .
.
Завершая анализ основных типов дифференциальных уравнений первого порядка, следует сказать, что существует большое количество таких уравнений, решения которых могут быть найдены только численными методами, например, методами Эйлера, Рунге-Кутта и другими.