Задачи для самостоятельного решения
-
Как связаны определители
с определителем
-
Решить уравнения:
а)
;
б)
в)
.
11. Вычислить определители по правилу треугольников и приведением матрицы к треугольному виду:
а)
;
б)
;
в)
.
12. Вычислить определители:
а)
;
б)
;
в)
;
г)
;
д)
.
-
Обратная матрица
Квадратная матрица А называется невырожденной, если ее определитель не равен нулю (в противном случае называется вырожденной).
Матрица
называется обратной для матрицы А,
если выполняются условия
.
Обратная матрица существует только для квадратных невырожденных матриц и находится по формуле
,
(1.5)
где
–
алгебраические дополнения элементов
матрицы
.
Примеры
-
Решить матричное уравнение
.
Р е ш е н и е.
Обозначим матрицы
,
.
Тогда исходное
уравнение запишется в виде
.
Вычислим определитель
Следовательно,
обратная матрица
существует
и
.
.
Тогда
.
-
Найти матрицу, обратную матрице
.
Р е ш е н и е.
Так как
то матрица А
невырожденная. Значит, обратная матрица
существует. Найдем ее по формуле (1.5).
Вычислим алгебраические дополнения:
,
Подставив полученные значения в формулу (1.5), получим
.
Убедимся, что
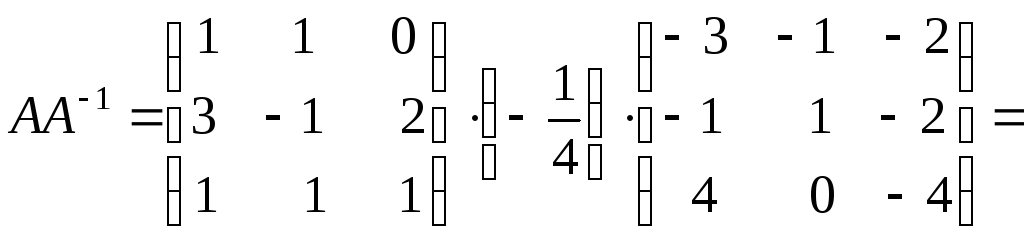
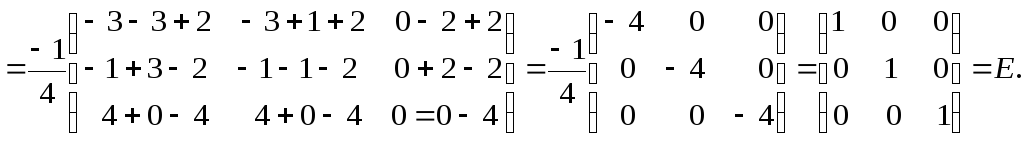
Задачи для самостоятельного решения
-
Решить матричные уравнения:
а)
,
б)
.
14. Показать, что
матрица А
невырожденная. Найти обратную матрицу
и проверить, что
:
а)
,
б)
,
в)
,
г)
,
д)
,
е)
.
1.4. Ранг матрицы
Минором к-го порядка матрицы
называется определитель к-го порядка,
составленный из элементов, стоящих на
пересечениях выбранных k
строк и k столбцов
матрицы А.
Рангом матрицы А называется
целое число, равное наивысшему порядку
не равных нулю миноров этой матрицы,
обозначается
Базисным минором матрицы называется любой не равный нулю минор матрицы, порядок которого равен ее рангу.
По определению ранг нулевой матрицы равен нулю. Ранг матрицы находят либо с помощью метода окаймляющих миноров, либо с помощью элементарных преобразований матрицы.
Элементарными преобразованиями матрицы называются:
-
перемена местами двух строк (двух столбцов);
-
умножение всех элементов какой-либо строки (столбца) на число, не равное нулю;
-
прибавление ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
-
вычеркивание строки (столбца), состоящей из нулей.
При элементарных преобразованиях матрицы ее ранг не изменяется.
С помощью элементарных преобразований матрицу приводят к такому виду, при котором легко находится базисный минор, порядок которого определяет ранг матрицы.
Видами таких матриц являются треугольная, трапециевидная, ступенчатая матрицы и др.
Примеры
13. Найти ранг матрицы А методом окаймляющих миноров, если
.
Р е ш е н и е. Возьмем минор второго порядка, не равный нулю
Вычислим окаймляющие его миноры третьего порядка:
Так как не существует
окаймляющих миноров третьего порядка,
отличных от нуля, то
-
Найти ранг матрицы с помощью элементарных преобразований, если
.
Р е ш е н и е. С помощью элементарных преобразований приведем матрицу к трапециевидному виду. Переход от одной матрицы к другой будем обозначать символом .
|
|
|
из второй строки, умноженной на 2, вычитаем первую строку; из третьей строки, умноженной на 2, вычитаем первую строку |
.
Последняя матрица имеет минор второго порядка, не равный нулю:
,
а все миноры третьего порядка равны
нулю. Следовательно,
.
-
Найти ранг матрицы при различных значениях параметра
.
Р е ш е н и е.
.
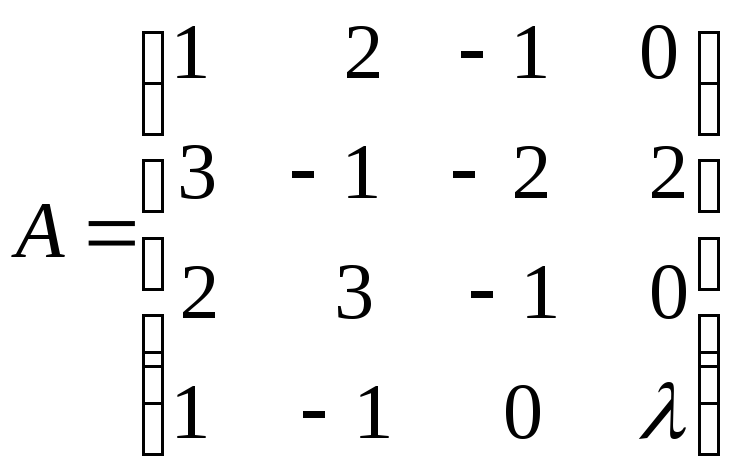
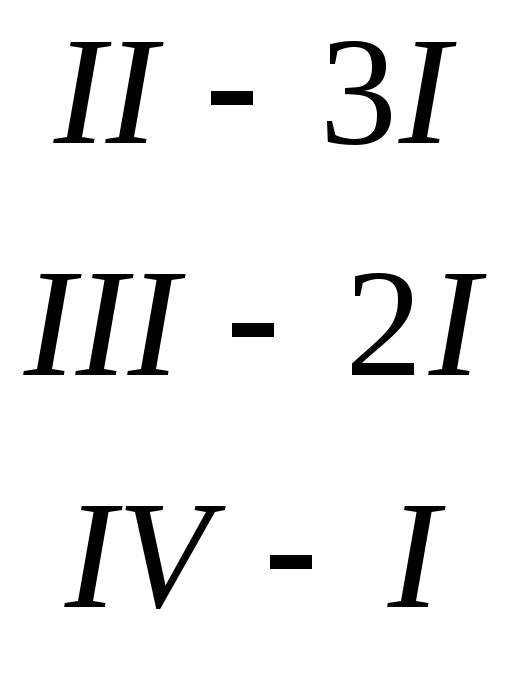
При
